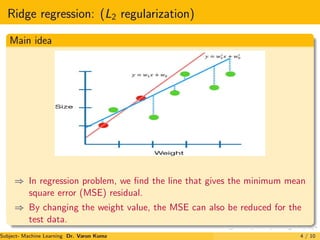
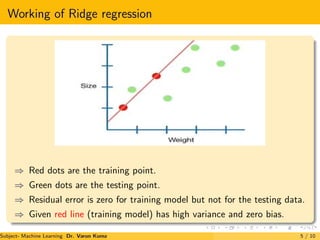
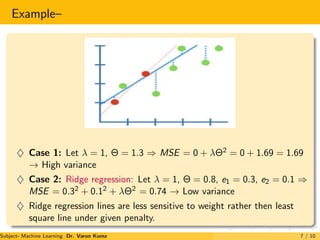
The document discusses regularization techniques for machine learning models called Ridge and Lasso regression. Ridge regression, also known as L2 regularization, introduces a small bias to models to minimize testing error by reducing variance. It works by adding penalties for large weights proportional to the square of the weight. Lasso regression, or L1 regularization, is similar but can exclude useless variables from models by setting some weights to zero. Both techniques aim to reduce overfitting and improve generalization to unlabeled data.

1. L2 and L1 Regularization/ Ridge and Lasso Regression
Subject- Machine Learning
Dr. Varun Kumar
Subject- Machine Learning Dr. Varun Kumar 1 / 10

2. Outlines
1 Problem of Overfitting
2 Ridge Regression
Main idea behind Ridge regression
Working of Ridge regression
How it can solve the unsolvable?
3 Lasso Regression
4 References
Subject- Machine Learning Dr. Varun Kumar 2 / 10

3. Problem of Overfitting
In real world scenario, the model should performed well for unlabeled or
unknown data.
Overfitted model works well for training data only.
By increasing the model complexity testing data also works well but
underperform for very high complexity.
Subject- Machine Learning Dr. Varun Kumar 3 / 10

4. Ridge regression: (L2 regularization)
Main idea
⇒ In regression problem, we find the line that gives the minimum mean
square error (MSE) residual.
⇒ By changing the weight value, the MSE can also be reduced for the
test data.
Subject- Machine Learning Dr. Varun Kumar 4 / 10

5. Working of Ridge regression
⇒ Red dots are the training point.
⇒ Green dots are the testing point.
⇒ Residual error is zero for training model but not for the testing data.
⇒ Given red line (training model) has high variance and zero bias.
Subject- Machine Learning Dr. Varun Kumar 5 / 10

6. Continued–
⇒ We introduce a small bias, so that MSE for test data could be
minimized.
⇒ From above figure
size = y − axis intercept + Slope × weight
⇒ From Ridge regression
MSE =
1
m
n+m
X
i=n+1
(yi − ˆ
f (xi ))2
+ λ × Θ2
(a) Θ → Slope of st line.
(b) λ → Penalty factor, 0 < λ < ∞
Subject- Machine Learning Dr. Varun Kumar 6 / 10

7. Example–
♦ Case 1: Let λ = 1, Θ = 1.3 ⇒ MSE = 0 + λΘ2 = 0 + 1.69 = 1.69
→ High variance
♦ Case 2: Ridge regression: Let λ = 1, Θ = 0.8, e1 = 0.3, e2 = 0.1 ⇒
MSE = 0.32 + 0.12 + λΘ2 = 0.74 → Low variance
♦ Ridge regression lines are less sensitive to weight rather then least
square line under given penalty.
Subject- Machine Learning Dr. Varun Kumar 7 / 10

8. Penalty factor λ
⇒ MSE = 1
m
Pn+m
i=n+1(yi − ˆ
f (xi ))2 + λ × Θ2 → Ridge regression
⇒ Higher the slope (Θ) → Size is more sensitive to the weight from
above figure.
⇒ Penalty= λ × Θ2
If λ = 0, Penalty=0
If λ1 = 1 and λ2 = 2, under constant penalty, Θ2 < Θ1.
If λ → ∞, under constant penalty, Slope → 0.
⇒ For very large λ, size becomes insensitive to the weight from above
figure.
Note: From above discussion Ridge regression has been discussed (size vs
weight), which is continuous variable. It can also be applicable for discrete
variable.
Subject- Machine Learning Dr. Varun Kumar 8 / 10

9. Lasso regression: L1 regularization
It is similar to the Ridge regression, but there are some differences
From Lasso regression
MSE =
1
m
n+m
X
i=n+1
(yi − ˆ
f (xi ))2
+ λ × |Θ|
(a) Θ → Slope of st line.
(b) λ → Penalty factor, 0 < λ < ∞
Difference between Ridge and Lasso regression
Lasso regression can exclude the useless variable from the equation.
Ridge regression include the variable in the equation, which are more
important.
Subject- Machine Learning Dr. Varun Kumar 9 / 10

10. References
E. Alpaydin, Introduction to machine learning. MIT press, 2020.
T. M. Mitchell, The discipline of machine learning. Carnegie Mellon University,
School of Computer Science, Machine Learning , 2006, vol. 9.
J. Grus, Data science from scratch: first principles with python. O’Reilly Media,
2019.
Subject- Machine Learning Dr. Varun Kumar 10 / 10