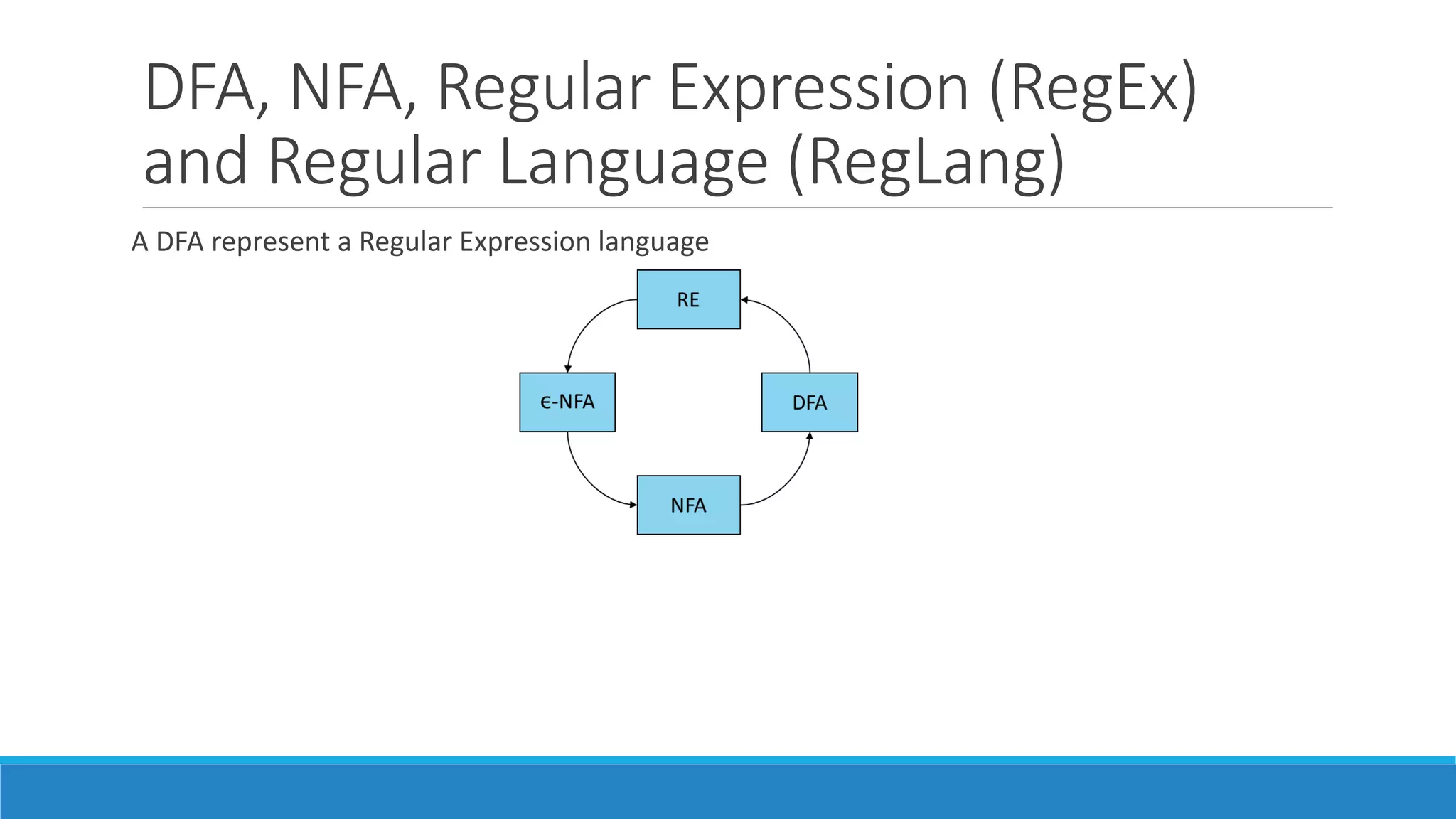
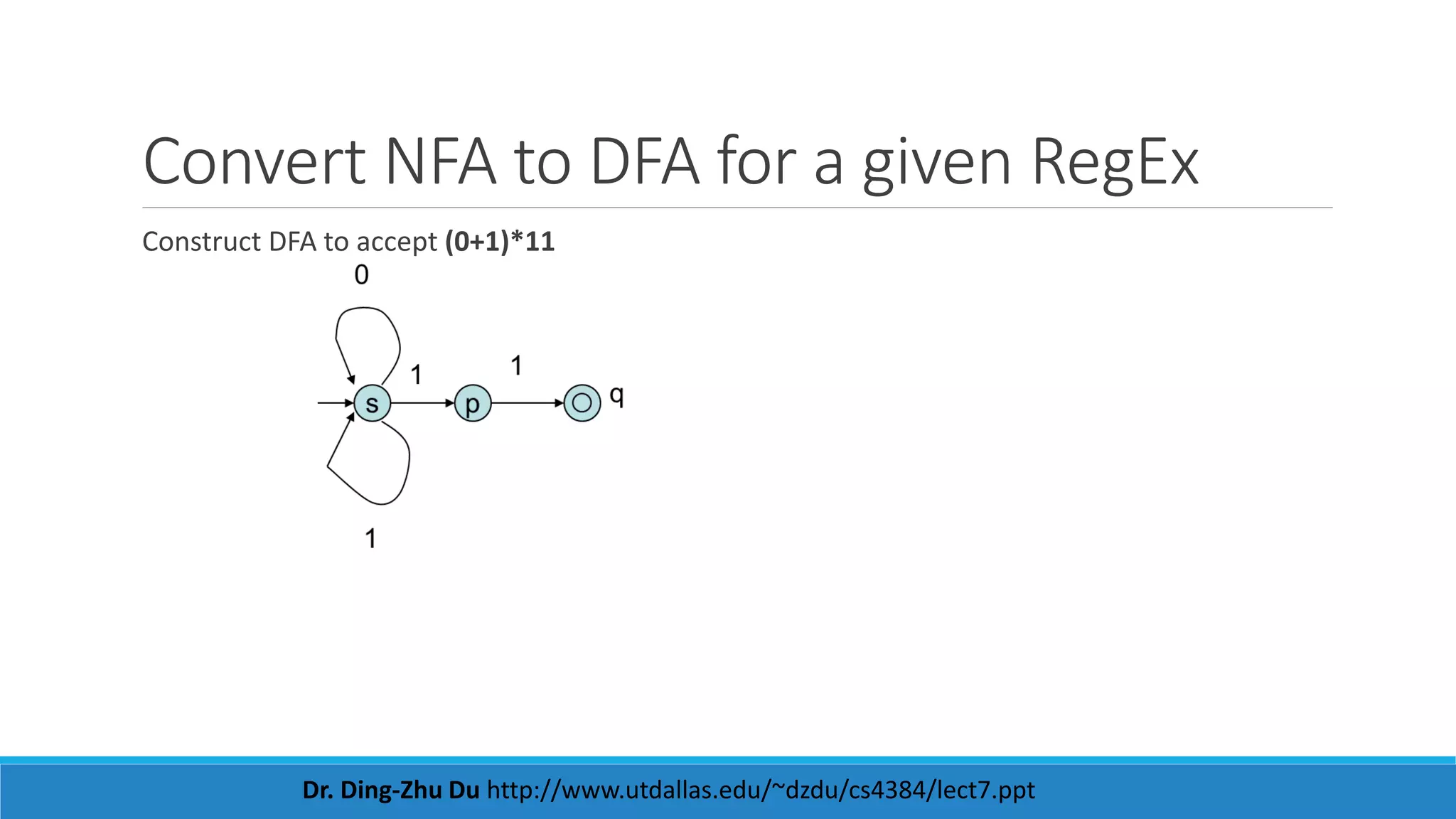
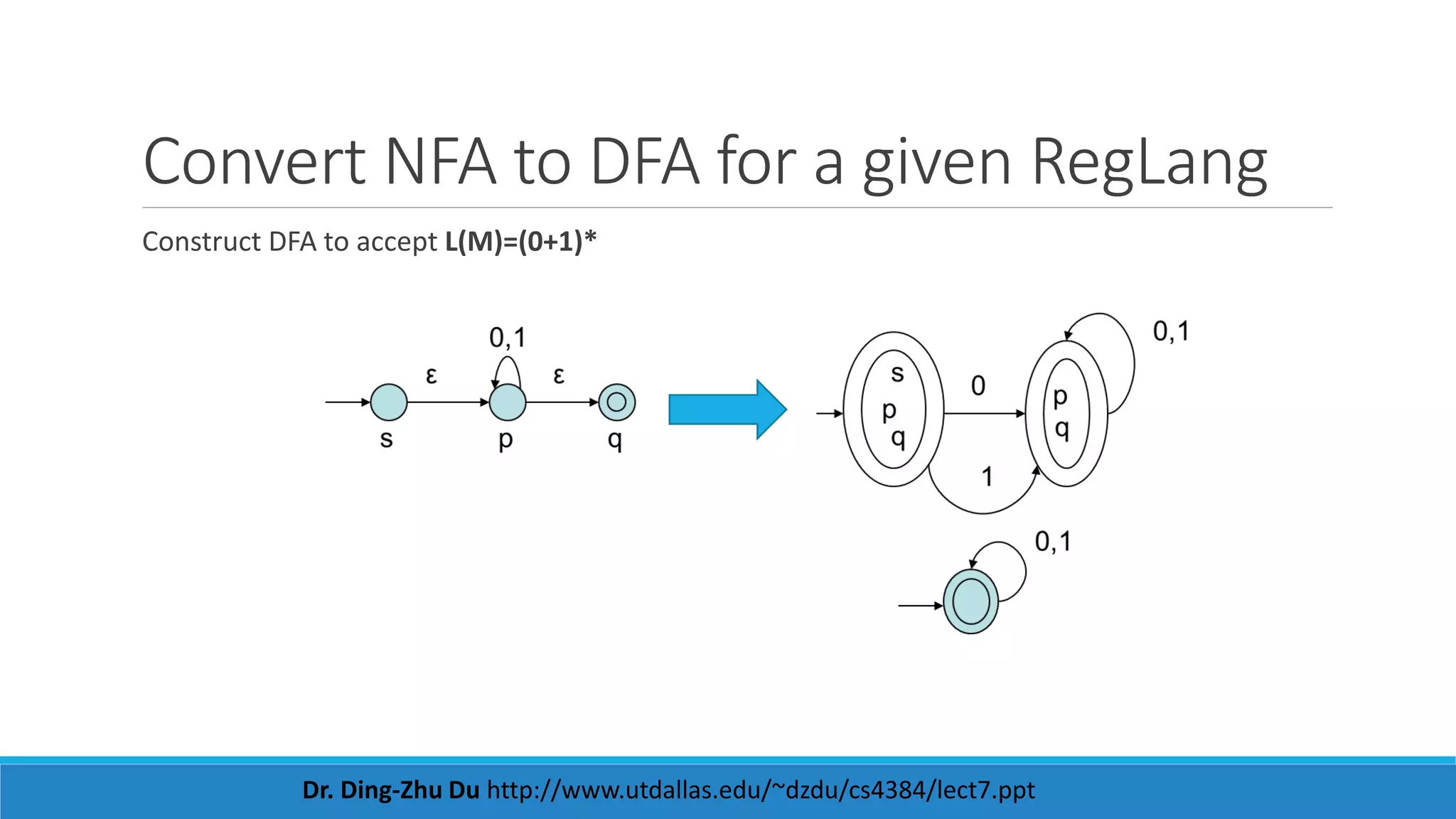
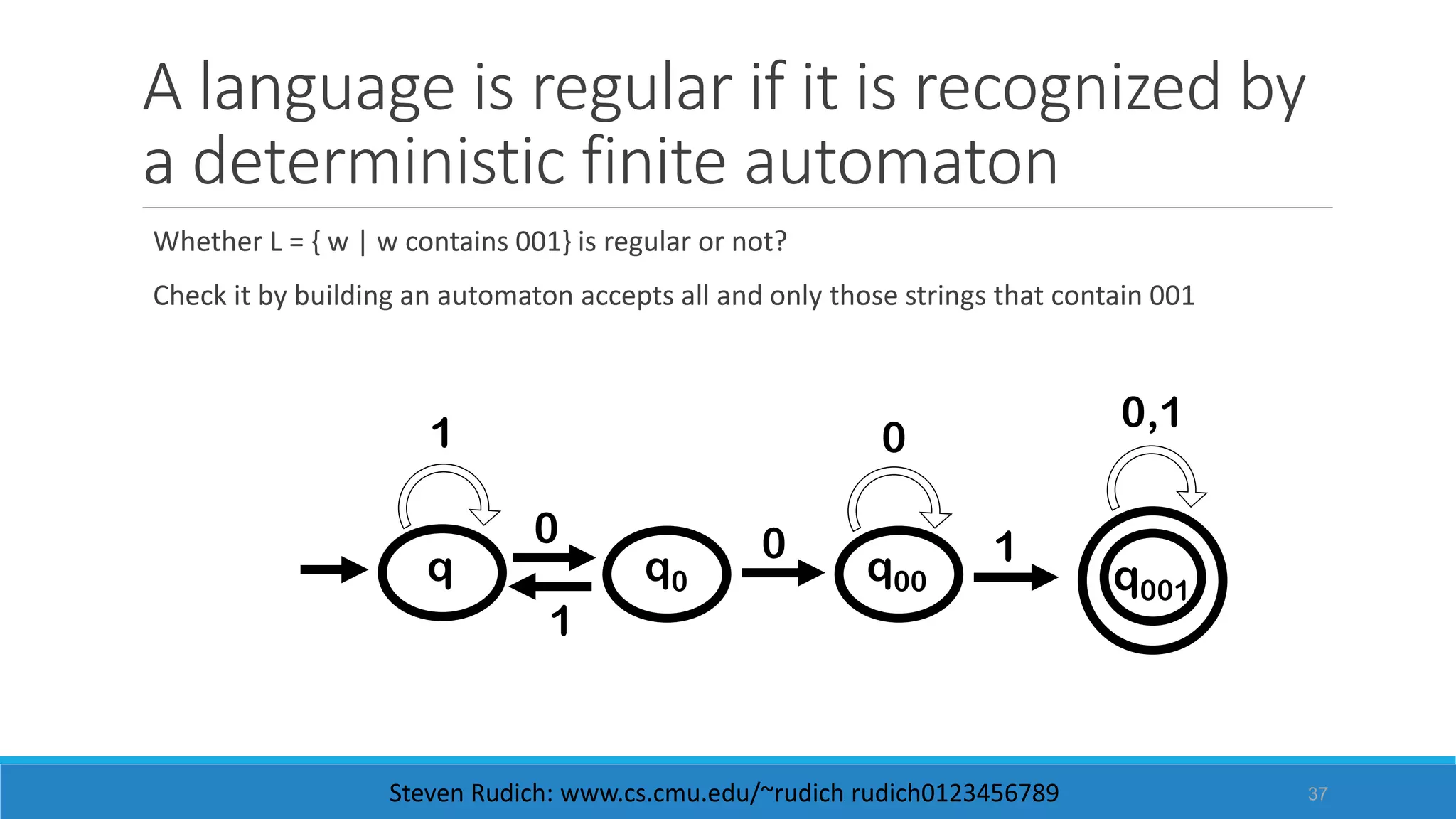
This document contains information about regular expressions and regular languages. It includes examples of regular expressions and their corresponding regular languages. It also discusses deterministic finite automata (DFAs) and non-deterministic finite automata (NFAs) and how to convert NFAs to equivalent DFAs. Additionally, it provides examples of constructing DFAs to recognize specific regular languages and expressions. Overall, the document serves as a tutorial on key concepts in automata theory and regular languages.