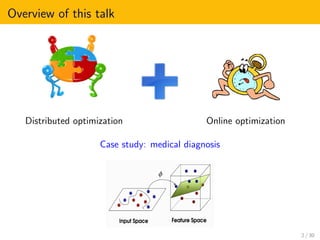
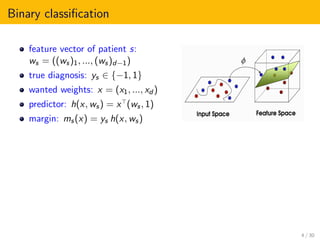
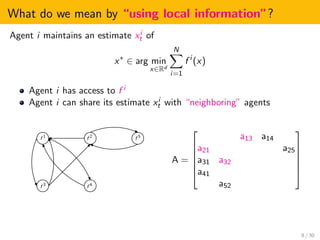
This document presents an overview of distributed online optimization over jointly connected digraphs. It discusses combining distributed convex optimization and online convex optimization frameworks. Specifically, it proposes a coordination algorithm for distributed online optimization over time-varying communication digraphs that are weight-balanced and jointly connected. The algorithm achieves sublinear regret bounds of O(sqrt(T)) under convexity and O(log(T)) under local strong convexity, using only local information and historical observations. This is an improvement over previous work that required fixed strongly connected digraphs or projection onto bounded sets.

1. Distributed online optimization over jointly connected
digraphs
David Mateos-N´u˜nez Jorge Cort´es
University of California, San Diego
{dmateosn,cortes}@ucsd.edu
Mathematical Theory of Networks and Systems
University of Groningen, July 7, 2014
1 / 30

2. Overview of this talk
Distributed optimization Online optimization
Case study: medical diagnosis
2 / 30

3. Motivation: a data-driven optimization problem
Medical findings, symptoms:
age factor
amnesia before impact
deterioration in GCS score
open skull fracture
loss of consciousness
vomiting
Any acute brain finding revealed on Computerized Tomography?
(-1 = not present, 1 = present)
“The Canadian CT Head Rule for patients with minor head injury”
3 / 30

4. Binary classification
feature vector of patient s:
ws = ((ws)1, ..., (ws)d−1)
true diagnosis: ys ∈ {−1, 1}
wanted weights: x = (x1, ..., xd )
predictor: h(x, ws) = x (ws, 1)
margin: ms(x) = ys h(x, ws)
4 / 30

5. Binary classification
feature vector of patient s:
ws = ((ws)1, ..., (ws)d−1)
true diagnosis: ys ∈ {−1, 1}
wanted weights: x = (x1, ..., xd )
predictor: h(x, ws) = x (ws, 1)
margin: ms(x) = ys h(x, ws)
Given the data set {ws}P
s=1, estimate x ∈ Rd by solving
min
x∈Rd
P
s=1
l(ms(x))
where the loss function l : R → R is decreasing and convex
4 / 30

6. Why distributed online optimization?
Why distributed?
information is distributed across group of agents
need to interact to optimize performance
Why online?
information becomes incrementally available
need adaptive solution
5 / 30

7. Review of
distributed convex optimization
6 / 30

8. A distributed scenario
In the diagnosis example health center i ∈ {1, . . . , N}
manages a set of patients Pi
f (x) =
N
i=1 s∈Pi
l(ysh(x, ws)) =
N
i=1
f i
(x)
7 / 30

9. A distributed scenario
In the diagnosis example health center i ∈ {1, . . . , N}
manages a set of patients Pi
f (x) =
N
i=1 s∈Pi
l(ysh(x, ws)) =
N
i=1
f i
(x)
Goal: best predicting model w → h(x∗, w)
min
x∈Rd
N
i=1
f i
(x)
using “local information”
7 / 30

10. What do we mean by “using local information”?
Agent i maintains an estimate xi
t of
x∗
∈ arg min
x∈Rd
N
i=1
f i
(x)
Agent i has access to f i
Agent i can share its estimate xi
t with “neighboring” agents
f 1
f 2
f 3
f 4
f 5
A =






a13 a14
a21 a25
a31 a32
a41
a52






8 / 30

11. What do we mean by “using local information”?
Agent i maintains an estimate xi
t of
x∗
∈ arg min
x∈Rd
N
i=1
f i
(x)
Agent i has access to f i
Agent i can share its estimate xi
t with “neighboring” agents
f 1
f 2
f 3
f 4
f 5
A =






a13 a14
a21 a25
a31 a32
a41
a52






Distributed algorithms: Tsitsiklis 84, Bertsekas and Tsitsiklis 95
Consensus: Jadbabaie et al. 03, Olfati-Saber, Murray 04, Boyd et al. 05
8 / 30

12. How do agents agree on the optimizer?
local minimization vs local consensus
9 / 30

13. How do agents agree on the optimizer?
local minimization vs local consensus
A. Nedi´c and A. Ozdaglar, TAC, 09
xi
k+1 = −ηkgi
k +
N
j=1
aij,k xj
k,
where gi
k ∈ ∂f i (xi
k) and Ak = (aij,k) is doubly stochastic
J. C. Duchi, A. Agarwal, and M. J. Wainwright, TAC, 12
9 / 30

14. Saddle-point dynamics
The minimization problem can be regarded as
min
x∈Rd
N
i=1
f i
(x) = min
x1,...,xN ∈Rd
x1=...=xN
N
i=1
f i
(xi
) = min
x∈(Rd )N
Lx=0
˜f (x),
(Lx)i
=
N
j=1
aij (xi
− xj
) ˜f (x) =
N
i=1
f i
(xi
)
10 / 30

15. Saddle-point dynamics
The minimization problem can be regarded as
min
x∈Rd
N
i=1
f i
(x) = min
x1,...,xN ∈Rd
x1=...=xN
N
i=1
f i
(xi
) = min
x∈(Rd )N
Lx=0
˜f (x),
(Lx)i
=
N
j=1
aij (xi
− xj
) ˜f (x) =
N
i=1
f i
(xi
)
Convex-concave augmented Lagrangian when L is symmetric
F(x, z) := ˜f (x) + γ
2 x L x + z L x,
Saddle-point dynamics
˙x = −
∂F(x, z)
∂x
= − ˜f (x) − γ Lx − Lz
˙z =
∂F(x, z)
∂z
= Lx
10 / 30

16. In the case of directed graphs
Weight-balanced ⇔ 1 L = 0 ⇔ L + L 0,
F(x, z) := ˜f (x) + γ
2 x L x + z L x
still convex-concave
11 / 30

17. In the case of directed graphs
Weight-balanced ⇔ 1 L = 0 ⇔ L + L 0,
F(x, z) := ˜f (x) + γ
2 x L x + z L x
still convex-concave
˙x = −
∂F(x, z)
∂x
= − ˜f (x) − γ 1
2 L + L x − L z (Non distributed!)
˙z =
∂F(x, z)
∂z
= Lx
J. Wang and N. Elia (with L = L), Allerton, 10
11 / 30

18. In the case of directed graphs
Weight-balanced ⇔ 1 L = 0 ⇔ L + L 0,
F(x, z) := ˜f (x) + γ
2 x L x + z L x
still convex-concave
˙x = −
∂F(x, z)
∂x
= − ˜f (x) − γ 1
2 L + L x − L z (Non distributed!)
changed to − ˜f (x) − γ Lx − Lz
˙z =
∂F(x, z)
∂z
= Lx
B. Gharesifard and J. Cort´es, CDC, 12
11 / 30

19. Review of
online convex optimization
12 / 30

20. Different kind of optimization: sequential decision making
In the diagnosis example:
Each round t ∈ {1, . . . , T}
question (features, medical findings): wt
decision (about using CT): h(xt, wt)
outcome (by CT findings/follow up of patient): yt
loss: l(yt h(xt, wt))
Choose xt & Incur loss ft(xt) := l(yt h(xt, wt))
13 / 30

21. Different kind of optimization: sequential decision making
In the diagnosis example:
Each round t ∈ {1, . . . , T}
question (features, medical findings): wt
decision (about using CT): h(xt, wt)
outcome (by CT findings/follow up of patient): yt
loss: l(yt h(xt, wt))
Choose xt & Incur loss ft(xt) := l(yt h(xt, wt))
Goal: sublinear regret
R(u, T) :=
T
t=1
ft(xt) −
T
t=1
ft(u) ∈ o(T)
using “historical observations”
13 / 30

22. Why regret?
If the regret is sublinear,
T
t=1
ft(xt) ≤
T
t=1
ft(u) + o(T),
then,
lim
T→∞
1
T
T
t=1
ft(xt) ≤ lim
T→∞
1
T
T
t=1
ft(u)
In temporal average, online decisions {xt}T
t=1 perform as well as best
fixed decision in hindsight
“No regrets, my friend”
14 / 30

23. Why regret?
What about generalization error?
Sublinear regret does not imply xt+1 will do well with ft+1
No assumptions about sequence {ft}; it can
follow an unknown stochastic or deterministic model,
or be chosen adversarially
15 / 30

24. Why regret?
What about generalization error?
Sublinear regret does not imply xt+1 will do well with ft+1
No assumptions about sequence {ft}; it can
follow an unknown stochastic or deterministic model,
or be chosen adversarially
In our example, ft := l(yt h(xt, wt)).
If some model w → h(x∗
, w) explains reasonably the data in
hindsight,
then the online models w → h(xt, w) perform just as well in average
15 / 30

25. Some classical results
Projected gradient descent:
xt+1 = ΠS(xt − ηt ft(xt)), (1)
where ΠS is a projection onto a compact set S ⊆ Rd , & f 2 ≤ H
Follow-the-Regularized-Leader:
xt+1 = arg min
y∈S
t
s=1
fs(y) + ψ(y)
16 / 30

26. Some classical results
Projected gradient descent:
xt+1 = ΠS(xt − ηt ft(xt)), (1)
where ΠS is a projection onto a compact set S ⊆ Rd , & f 2 ≤ H
Follow-the-Regularized-Leader:
xt+1 = arg min
y∈S
t
s=1
fs(y) + ψ(y)
Martin Zinkevich, 03
(1) achieves O(
√
T) regret under convexity with ηt = 1√
t
Elad Hazan, Amit Agarwal, and Satyen Kale, 07
(1) achieves O(log T) regret under p-strong convexity with ηt = 1
pt
Others: Online Newton Step, Follow the Regularized Leader, etc.
16 / 30

27. Done with the review
Now... we combine the two frameworks
Previous work and limitations
our coordination algorithm in the online case
theorems of O(
√
T) & O(log T) agent regrets
simulations
outline of the proof
17 / 30

28. Combining both frameworks
18 / 30

29. Resuming the diagnosis example:
Health center i ∈ {1, . . . , N} takes care of a set of patients Pi
t at time t
f i
(x) =
T
t=1 s∈Pi
t
l(ysh(x, ws)) =
T
t=1
f i
t (x)
19 / 30

30. Resuming the diagnosis example:
Health center i ∈ {1, . . . , N} takes care of a set of patients Pi
t at time t
f i
(x) =
T
t=1 s∈Pi
t
l(ysh(x, ws)) =
T
t=1
f i
t (x)
Goal: sublinear agent regret
Rj
(u, T) :=
T
t=1
N
i=1
f i
t (xj
t ) −
T
t=1
N
i=1
f i
t (u) ≤ o(T)
using “local information” & “historical observations”
19 / 30

31. Challenge: Coordinate hospitals
f 1
t f 2
t
f 3
t f 4
t
f 5
t
Need to design distributed online algorithms
20 / 30

32. Previous work on consensus-based online algorithms
F. Yan, S. Sundaram, S. V. N. Vishwanathan and Y. Qi, TAC
Projected Subgradient Descent
log(T) regret (local strong convexity & bounded subgradients)√
T regret (convexity & bounded subgradients)
Both analysis require a projection onto a compact set
S. Hosseini, A. Chapman and M. Mesbahi, CDC, 13
Dual Averaging
√
T regret (convexity & bounded subgradients)
General regularized projection onto a convex closed set.
K. I. Tsianos and M. G. Rabbat, arXiv, 12
Projected Subgradient Descent
Empirical risk as opposed to regret analysis
Limitations: Communication digraph in all cases
is fixed and strongly connected
21 / 30

33. Our contributions (informally)
time-varying communication digraphs under B-joint connectivity &
weight-balanced
unconstrained optimization (no projection step onto a bounded set)
log T regret (local strong convexity & bounded subgradients)
√
T regret (convexity & β-centrality with β ∈ (0, 1] & bounded
subgradients)
22 / 30

34. Our contributions (informally)
time-varying communication digraphs under B-joint connectivity &
weight-balanced
unconstrained optimization (no projection step onto a bounded set)
log T regret (local strong convexity & bounded subgradients)
√
T regret (convexity & β-centrality with β ∈ (0, 1] & bounded
subgradients)
x∗
x
−ξx
f i
t is β-central in Z ⊆ Rd X∗,
where X∗ = x∗ : 0 ∈ ∂f i
t (x∗) ,
if ∀x ∈ Z, ∃x∗ ∈ X∗ such that
−ξx (x∗ − x)
ξx 2 x∗ − x 2
≥ β,
for each ξx ∈ ∂f i
t (x).
22 / 30

35. Coordination algorithm
xi
t+1 = xi
t − ηt gxi
t
Subgradient descent on previous local objectives, gxi
t
∈ ∂f i
t
23 / 30

36. Coordination algorithm
xi
t+1 = xi
t − ηt gxi
t
+ σ γ
N
j=1,j=i
aij,t xj
t − xi
t
Proportional (linear) feedback on disagreement with neighbors
23 / 30

37. Coordination algorithm
xi
t+1 = xi
t − ηt gxi
t
+ σ γ
N
j=1,j=i
aij,t xj
t − xi
t +
N
j=1,j=i
aij,t zj
t − zi
t
zi
t+1 = zi
t − σ
N
j=1,j=i
aij,t xj
t − xi
t
Integral (linear) feedback on disagreement with neighbors
23 / 30

38. Coordination algorithm
xi
t+1 = xi
t − ηt gxi
t
+ σ γ
N
j=1,j=i
aij,t xj
t − xi
t +
N
j=1,j=i
aij,t zj
t − zi
t
zi
t+1 = zi
t − σ
N
j=1,j=i
aij,t xj
t − xi
t
Union of graphs over intervals of length B is strongly connected.
f 1
t f 2
t
f 3
t f 4
t
f 5
t
time t time t + 1
a14,t+1a41,t+1
time t + 2
23 / 30

39. Coordination algorithm
xi
t+1 = xi
t − ηt gxi
t
+ σ γ
N
j=1,j=i
aij,t xj
t − xi
t +
N
j=1,j=i
aij,t zj
t − zi
t
zi
t+1 = zi
t − σ
N
j=1,j=i
aij,t xj
t − xi
t
Compact representation
xt+1
zt+1
=
xt
zt
− σ
γLt Lt
−Lt 0
xt
zt
− ηt
˜gxt
0
23 / 30

40. Coordination algorithm
xi
t+1 = xi
t − ηt gxi
t
+ σ γ
N
j=1,j=i
aij,t xj
t − xi
t +
N
j=1,j=i
aij,t zj
t − zi
t
zi
t+1 = zi
t − σ
N
j=1,j=i
aij,t xj
t − xi
t
Compact representation & generalization
xt+1
zt+1
=
xt
zt
− σ
γLt Lt
−Lt 0
xt
zt
− ηt
˜gxt
0
vt+1 = (I − σE ⊗ Lt)vt − ηtgt,
23 / 30

41. Theorem (DMN-JC)
Assume that
{f 1
t , ..., f N
t }T
t=1 are convex functions in Rd
with H-bounded subgradient sets,
nonempty and uniformly bounded sets of minimizers, and
p-strongly convex in a suff. large neighborhood of their minimizers
The sequence of weight-balanced communication digraphs is
nondegenerate, and
B-jointly-connected
E ∈ RK×K is diagonalizable with positive real eigenvalues
Then, taking σ ∈
˜δ
λmin(E)δ , 1−˜δ
λmax(E)dmax
and ηt = 1
p t ,
Rj
(u, T) ≤ C( u 2
2 + 1 + log T),
for any j ∈ {1, . . . , N} and u ∈ Rd
24 / 30

42. Theorem (DMN-JC)
Assume that
{f 1
t , ..., f N
t }T
t=1 are convex functions in Rd
with H-bounded subgradient sets,
nonempty and uniformly bounded sets of minimizers, and
p-strongly convex in a suff. large neighborhood of their minimizers
The sequence of weight-balanced communication digraphs is
nondegenerate, and
B-jointly-connected
E ∈ RK×K is diagonalizable with positive real eigenvalues
Substituting strong convexity by β-centrality, for β ∈ (0, 1],
Rj
(u, T) ≤ C u 2
2
√
T,
for any j ∈ {1, . . . , N} and u ∈ Rd
24 / 30

43. Simulations:
acute brain finding revealed on Computerized Tomography
25 / 30

44. Simulations
Agents’ estimates
0 20 40 60 80 100 120 140 160 180 200
−0.5
0
0.5
1
1.5
2
{ xi
t,7}N
i=1
0 20 40 60 80 100 120 140 160 180 200
0
1
2
time, t
Centralized
Average regret
0 20 40 60 80 100 120 140 160 180 200
10
−3
10
−2
10
−1
10
0
10
1
time horizon, T
maxj 1/T Rj
x∗
T ,
N
i f i
t
T
t=1
Proportional-Integral
disagreement feedback
Proportional
disagreement feedback
Centralized
f i
t (x) =
s∈Pi
t
l(ysh(x, ws)) + 1
10 x 2
2
where
l(m) = log 1 + e−2m
26 / 30

45. Outline of the proof
Analysis of network regret
RN (u, T) :=
T
t=1
N
i=1
f i
t (xi
t ) −
T
t=1
N
i=1
f i
t (u)
ISS with respect to agreement
ˆLKvt 2 ≤ CI v1 2 1 −
˜δ
4N2
t−1
B
+ CU max
1≤s≤t−1
us 2,
Agent regret bound in terms of {ηt}t≥1 and initial conditions
Boundedness of online estimates under β-centrality (β ∈ (0, 1] )
Doubling trick to obtain O(
√
T) agent regret
Local strong convexity ⇒ β-centrality
ηt = 1
p t to obtain O(log T) agent regret
27 / 30

46. Conclusions and future work
Conclusions
Distributed online convex optimization over jointly connected
digraphs,
submitted to IEEE Transactions on Network Science and Engineering
(can be found in the webpage of Jorge Cort´es)
Relevant for regression & classification that play a crucial role in
machine learning, computer vision, etc.
Future work
Refine guarantees under
model for evolution
of objective functions
28 / 30

47. Future directions in data-driven optimization problems
Distributed strategies for...
feature selection
semi-supervised learning
29 / 30

48. Thank you for listening!
Contact: David Mateos-N´u˜nez and Jorge Cort´es, at UC San Diego
30 / 30