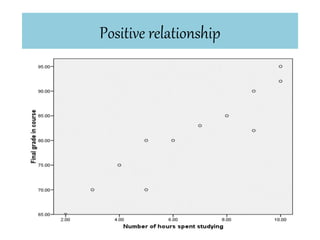
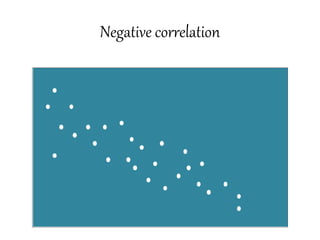
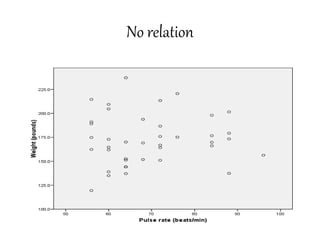
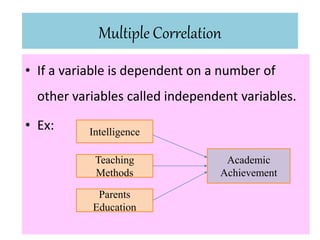
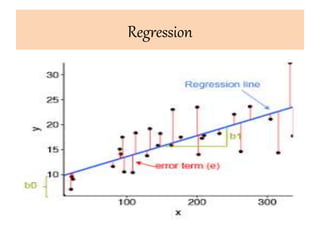
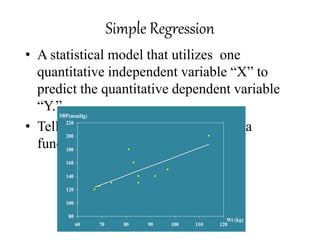
This document discusses correlation coefficient and regression analysis. It defines correlation coefficient as representing the relationship between two variables with a straight line and ranging from -1 to 1. Regression analysis predicts changes in a dependent variable from changes in independent variables. The coefficient of determination measures the proportion of variance explained by the regression model. Multiple regression uses two or more explanatory variables to predict an outcome.

1. Correlation Coefficient
&
Regression Analysis

2. Correlation coefficient
• Relationship between two variables can be represented
graphically by a straight line, it is known as linear
correlation.
• Correlation can be positive, negative or zero correlation.
• Express the degree of relationship b/w two variables is
called coefficient of correlation
• -1 ( indicating perfect negative correlation) to +1 (
indicating perfect positive correlation)
• Zero means no correlation

3. Positive relationship

4. Negative correlation

5. No relation

6. Simple Correlation coefficient (r)
• It is also called Pearson's correlation or product
moment correlation
coefficient.
• It measures the nature and strength between two
variables of
the quantitative type.
• The sign of r denotes the nature of association while
the value of r denotes the strength of association.
• If the sign is +ve this means the relation is direct
• While if the sign is -ve this means an inverse or indirect
relationship

7. • The value of r ranges between ( -1) and ( +1)
• The value of r denotes the strength of the
association as illustrated
by the following diagram.
• The range of the correlation coefficient is
1 to 1. If x and y have a strong positive
linear correlation, r is close to 1

9. • If r = Zero this means no association or
correlation between the two variables.
• If 0 < r < 0.25 = weak correlation.
• If 0.25 ≤ r < 0.75 = intermediate correlation.
• If 0.75 ≤ r < 1 = strong correlation.
• If r = l = perfect correlation.

10. Multiple Correlation
• If a variable is dependent on a number of
other variables called independent variables.
• Ex:
Academic
Achievement
Intelligence
Teaching
Methods
Parents
Education

11. Regression

12. Regression
• The coefficient of correlation tells us the way in
which two variables are related to each others.
• Coefficient of correlation b/w two variables
cannot predict the change in one variable in
systematic way, with the change in the other
variable.
• Regression help in the task of prediction.
• The process of predicting variable Y using
variable X
• Tells you how values in y change as a function of
changes in values of x

13. Coefficient of Determination
• The coefficient of determination r2 is the ratio
of the explained variation to the total variation.
That is,
•
Example:
The correlation coefficient for the data that
represents the number of hours students watched
television and the test scores of each student is r =
0.831. Find the coefficient of determination.
•
2 Explained variation
Total variation
r 
2 2
( 0.831)
r   0.691


14. Uses of Regression Analysis
• Regression analysis helps in establishing a
functional relationship between two or more
variables.
• Since most of the problems of psychology
analysis are based on cause and effect
relationships, the regression analysis is a highly
valuable tool in education and psychology
research.
• Regression analysis predicts the values of
dependent variables from the values of
independent variables

15. Simple Regression
• A statistical model that utilizes one
quantitative independent variable “X” to
predict the quantitative dependent variable
“Y.”
• Tells you how values in y change as a
function of changes in values of x
80
100
120
140
160
180
200
220
60 70 80 90 100 110 120
Wt (kg)
SBP(mmHg)

16. Multiple Regression
• A statistical model that utilizes two or more
quantitative and qualitative explanatory
variables (x1,..., xp) to predict a quantitative
dependent variable Y.
• Multiple regression analysis is a
straightforward extension of simple regression
analysis which allows more than one
independent variable

17. R Squared
•R-squared is the percentage of the response variable
variation that is explained by a linear model. Or:
•R-squared = Explained variation / Total variation
•R-squared is always between 0 and 100%:
• 0% indicates that the model explains none of the
variability of the response data around its mean.
• 100% indicates that the model explains all the
variability of the response data around its mean.

18. • The standard error measures the scatter in the
actual data around the estimate regression line.
• Standard Error is calculated by taking the
square root of the average prediction error.
• Standard Error = SSE
• n-k
• Where n is the number of observations in the
sample and k is the total number of variables in
the model
Standard Error of Regression