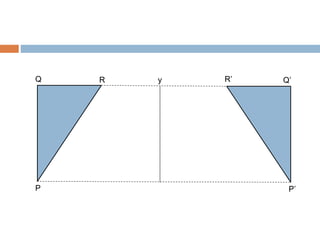
Refleksi atau pencerminan adalah transformasi yang memindahkan setiap titik pada bidang dengan menggunakan sifat bayangan cermin dari titik-titik yang akan dipindahkan. Refleksi dapat dilakukan terhadap sumbu koordinat, pusat, garis, atau titik tertentu. Contohnya refleksi terhadap sumbu Y akan mengubah koordinat x tetapi mengubah tanda koordinat y.

1. REFLEKSI /
PENCERMINAN

2. Pengertian
Suatu transformasi yang memindahkan setiap
titik pada bidang dengan menggunakan sifat
bayangan cermin dari titik – titik yang akan
dipindahkan

3. Q R
P
R’ Q’
P’
y

4. Materi
 Sumbu X atau Y = 0 adalah P(x, y) → P’(x, -y)
 Sumbu Y atau X = 0 adalah P(x, y) → P’(-x, y)
 Pusat O adalah P(x, y) → P’(-x, -y)
 Garis x = h adalah P(x, y) → P’(2h –x, y)
 Garis y = k adalah P(x, y) → P’(x, 2k – y)
 Garis Y = x adalah P(x, y) → P’(y, x)
 Garis Y = - x adalah P(x,y) → P’(-y, -x)
 Titik (h, k) adalah P(x, y) → P’( 2h – x, 2k – y)

5.  Sumbu X atau Y = 0 adalah P(x, y) → P’(x, -y)
P(2, 3) → sumbu x atau y = 0
P(x, y) → P’(x, -y)
P(2, 3) → P’(2,-3)
 Sumbu Y atau X = 0 adalah P(x, y) → P’(-x, y)
P(6, 3) → sumbu Y atau X = 0
P(x, y) → P’(-x, y)
P(6, 3) → P’(-6, 3)

6.  Pusat O adalah P(x, y) → P’(-x, -y)
P(-9, 3) → Pusat O P’(-x, -y)
P(x, y) → P’(-x, -y)
P(9, 3) → P’(-9, -3)
 Garis x = h adalah P(x, y)  𝑃′
(2h – x, y)
P(4, 4)  Garis x = h, x = 1adalah
𝑃′(2h – x, y)
P(x, y)  𝑃′ (2h – x, y)
P(4, 4)  𝑃′( 2 - 4, 4)  𝑃′(-2, 4)

7. Garis y = k adalah P(x, y)  𝑃′ 𝑥, 2𝑘 − 𝑦
P(2, 3)  garis y = k , k = 1 adalah P(x, y) 
𝑃′
𝑥, 2𝑘 − 𝑦
P(x, y)  𝑃′
𝑥, 2𝑘 − 𝑦
P(2, 3)  𝑃′
2, 2 − 3  𝑃′
(2, -1)
 Garis Y = x adalah P(x, y) → 𝑃′
(y, x)
P(-11, 6) → Garis Y = X adalah P(x, y) → P’(y, x)
P(x, y) → P’(y, x)
P(-8, 6) → P’(-8, 6)

8.  Garis Y = - x adalah P(x,y) → P’(-y, -x)
P(-12, -4) → Garis Y = - x adalah P(-y, -x)
P(x, y) → P’(-y, -x)
P(-3, -4) →P’(3, 4)
Titik (h, k) adalah P(x, y) → P’( 2h – x, 2k – y)
Jika diketahui x = 4 dan y = 4
P(x, y) → P’( 2h – x, 2k – y)
P(2, 2) → P’(2h – x, 2k – y)
P(2, 2) → P’(2(4) – 2, 2(4) – 2)
P(2, 2) → P’(8-2, 8-3)
P(2, 2) → P’(6, 6)

9. Latihan Soal
Tentukan bayangannya jika :
1. Titik A(7, 4) dicerminkan kedalam sumbu Y
2. Titik B(-4, 3) dicerminkan kedalam sumbu X
3. Titik C(-3, 2) dicerminkan terhadap pusat O
4. Jika titik A(8, 9) dicerminkan terhadap garis x = 3
5. Jika titik A(5, 6) dicerminkan terhadap garis y = 5
6. Titik D(2, -7) dicerminkan terhadap y = x
7. Titik E(-11, 2) dicerminkan terhadap y = -x
8. Titik F(2, 6) dicerminkan terhadap garis x = 2 & y = 4

10. 1. Sumbu X atau Y = 0 adalah P(x, y) → P’(x, -y)
P(7, 4) → sumbu x atau y = 0
P(x, y) → P’(x, -y)
P(7, 4) → P’(7,-4)
2. Sumbu Y atau X = 0 adalah P(x, y) → P’(-x, y)
P(-4, 3) → sumbu Y atau X = 0
P(x, y) → P’(-x, y)
P(-4, 3) → P’(4, 3)

11. 3. Pusat O adalah P(x, y) → P’(-x, -y)
P(-3, 2) → Pusat O P’(-x, -y)
P(x, y) → P’(-x, -y)
P(-3, 2) → P’(3, -2)
4. Garis x = h adalah P(x, y)  𝑃′ (2h – x, y)
P(8, 5)  Garis x = 3 adalah 𝑃′(2h – x, y)
P(x, y)  𝑃′ (2h – x, y)
P(8, 5)  𝑃′(6 – 8, 5)  𝑃′(-2, 5)

12. 5. Garis y = k adalah P(x, y)  𝑃′ 𝑥, 2𝑘 − 𝑦
P(5, 6)  garis y = 5 adalah P(x, y)  𝑃′
𝑥, 2𝑘 − 𝑦
P(x, y)  𝑃′ 𝑥, 2𝑘 − 𝑦
P(5, 6)  𝑃′ 5, 10 − 6  𝑃′(5, 4)
6. Garis Y = x adalah P(x, y) → 𝑃′(y, x)
P(-11, 6) → Garis Y = X adalah P(x, y) → P’(y, x)
P(x, y) → P’(y, x)
P(-11, 6) → P’(6, -11)

13. 7. Titik E(-11, 2) dicerminkan terhadap y = -x
P(-11, 2) → Garis Y = - x adalah P(-y, -x)
P(x, y) → P’(-y, -x)
P(-11, 2) →P’(11, -2)
8. Titik (h, k) adalah P(x, y) → P’( 2h – x, 2k – y)
Jika diketahui x = 2 dan y = 4
P(x, y) → P’( 2h – x, 2k – y)
P(2, 6) → P’(2h – x, 2k – y)
P(2, 6) → P’(2(2) – 2, 2(4) – 3)
P(2, 6) → P’(4-2, 8-3)
P(2, 6) → P’(2. 5)