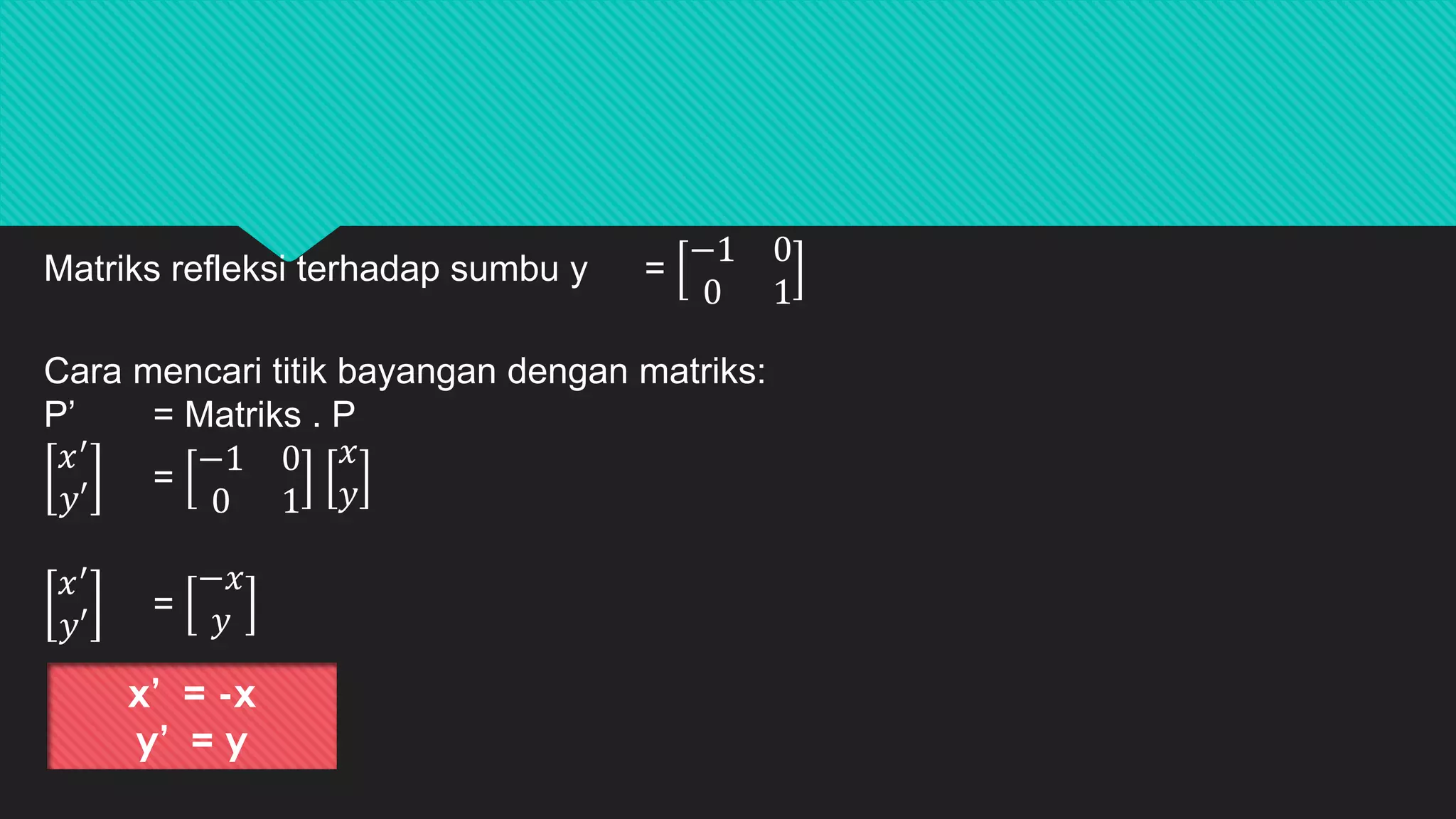
Dokumen ini membahas tentang translasi dan refleksi titik serta kurva dalam koordinat, termasuk cara menghitung koordinat setelah translasi dan persamaan baru setelah refleksi. Contoh-contoh yang diberikan memperlihatkan bagaimana mengaplikasikan metode translasi dan refleksi pada berbagai bentuk geometris. Selain itu, ditunjukkan juga penggunaan matriks dalam menentukan hasil transformasi tersebut.

1. KELOMPOK 1
C
Awan Rahmadewi (07)
Ihsan Putrananda (20)
Kurnia Yuliyanti Rahayu (23)
Muhammad Zufar (29)

2. Translasi Translasi Titik
Translasi Kurva
Refleksi Refleksi Titik dan Kurva terhadap
Sumbu X
Refleksi Titik dan Kurva terhadap
Sumbu Y

3. Translasi Titik
Jika translasi T =
푎
푏
memetakan titik P(x,y) keP´(x’,y’)
maka x’ = x + a dan y’ = y + b
ditulis dalam bentuk matrik:
푥′
푦′
=
푥
푦 +
푎
푏

4. Contoh 1
Diketahui segitiga OAB dengan koordinat titik O(0,0), A(3,0) dan
B(3,5). Tentukan koordinat bayangan segitiga OAB tersebut bila
ditranslasi oleh T =
1
3

5. Jawaban
(0,0) → (0 + 1, 0 + 3)
0’(1,3)
(3,0) → (3 + 1, 0 + 3)
A’(4,3)
(3,5) → (3 + 1, 5 + 3)
B’(4,8)
X
y
O
푇 =
1
3
푇 =
1
3
푇 =
1
3

6. Contoh 2
Dengan translasi
푎
푏
, peta dari titik (2a+b, b-a) adalah (4,1).
Dengan demikian nilai (a+2b) sama dengan

7. Jawaban
(2a+b, b-a) +
푎
푏
=(4,1)
(2a+b+a) = 4
3a + b = 4
(b-a+b) = 1
2b – a = 1
Cara Subsitusi
3a + b = 4 x1
-a + 2b= 1 x3
3a + b = 4
-3a + 6b = 3 +
7b = 7
b = 1
3a + 1 = 4
3a = 3
a = 1
Jadi (a + 2b) = 1 + 2(1) = 3

8. Translasi Kurva
Jika suatu kurva ditranslasi maka bentuk kurvanya tidak berubah,tetapi yang
berubah hanya posisinya. Adanya pergeseran posisi mengakibatkan perubahan
persamaan kurva.
Jika kurva ditranslasi oleh (a,b) dan titik (x1,y1) adalah titik pada kurva maka
persamaannya adalah :
X = X1+a ~ X1= X – a
Y = Y1+b ~ Y1 = Y – b
Persamaan kurva baru menjadi :
y – b = f(x – a)

9. Contoh 1
Dengan translasi
3
−2
parabola dengan persamaan y = x2 + 1 mempunyai
peta ...
Jawab :
y + 2 = (x – 3)2 + 1
y + 2 = x2 – 6x + 9 + 1
y + 2 = x2 – 6x + 10
y = x2 – 6x + 8

10. Contoh 2
Garis 3x+2y-3 = 0 ditranslasi oleh (4 2). Petanya adalah ...
Jawab:
3 (x – 4) + 2 (y – 2) – 3 = 0
3x – 12 + 2y – 4 – 3 = 0
3x + 2y – 19 = 0

11. Refleksi Titik dan Kurva terhadap Sumbu X
Transformasi refleksi terhadap
sumbu x dapat dinotasikan
dengan Msb-x. Misal titik x1,,y1
terletak pada kurva y f(x) dan
direfleksikan terhadap sumbu x.

12. Matriks refleksi terhadap sumbu x =
1 0
0 −1
Refleksi titik terhadap sumbu x (secara aljabar) : 푥1,, 푦1
푀푠푏−푥
푥1 , −푦1
Refleksi kurva terhadap sumbu x : y = f(x)
푀푠푏−푥
y = - f(x)

13. Contoh 1
Titik (-3,-4) direfleksikan ke sumbu x. Hasilnya adalah titik...
Jawab :
Cara Matriks :
풙′
풚′ =
ퟏ ퟎ
ퟎ −ퟏ
풙
풚
풙′
풚′ =
ퟏ ퟎ
ퟎ −ퟏ
−ퟑ
−ퟒ
풙′
풚′ =
−ퟑ
ퟒ
Cara Aljabar :
풙′, 풚′ = 풙, −풚
풙′, 풚′ = (-3 , 4)

14. Contoh 2
Parabola y = x2 − 2 direfleksikan ke sumbu x, petanya adalah...
Jawab :
y = f(x)
푀푠푏−푥
y’ = - f(x)
y = 푥2 − 2
푀푠푏−푥
y’ = -푥2 + 2

15. Refleksi Titik dan Kurva terhadap Sumbu Y
Transformasi refleksi terhadap
sumbu y dapat dinotasikan dengan
Msb-y.
Dengan refleksi terhadap sumbu y :
Titik (x,y) dipetakan ke (x’,y’)
dengan :
x’ = - x dan y’ = y
Maka 푥, 푦
푀푠푏−푦
−푥 , 푦

16. (x,y) merupakan titik pada y = f(x).
Karena x = - x’ dan y = y’
Maka :
y = f (x)
푀푠푏−푦
y = f (-x)

17. Matriks refleksi terhadap sumbu y =
−1 0
0 1
Cara mencari titik bayangan dengan matriks:
P’ = Matriks . P
푥′
=
푦′
−1 0
0 1
푥
푦
푥′
푦′
=
−푥
푦
x’ = -x
y’ = y

18. Contoh 1
Titik (-3, -4) direfleksikan ke sumbu y. Hasilnya adalah titik ...
Jawab :
Cara aljabar :
풙′, 풚′ = −풙, 풚
풙′, 풚′ = (3 , -4)
Cara Matriks :
푥′
푦′
=
−1 0
0 1
−3
−4
=
3
−4

19. Contoh 2
Parabola y = x2 – 2 direfleksikan ke sumbu y, petanya adalah ...
Jawab :
푥′
푦′
=
−1 0
0 1
푥
푦
푥′
푦′
=
−푥
푦
x’ = -x
y’ = y
y = x2 – 2
y’ = (x’)2 – 2
y = (-x)2 – 2
y = x2 – 2