This document contains details of a mathematics lesson plan for 9th standard including the name of the teacher, school, subject, unit and sub-unit being covered. The key point being taught is that triangles formed by two intersecting lines will always have the same area. The lesson plan outlines the curriculum statement, content analysis, learning outcomes, prerequisites, teaching resources, classroom interactions and activities to help students understand and apply the concept that triangles formed by two intersecting lines will always have the same area.

1. Name of the teacher : Reenamol K Standard : IX
Name of the School : Division :
Subject : Mathematics Strength :
Unit : ]c¸fhv Date :
Sub Unit : amdm¯]c¸fhv Duration :
Curricular Statement
c−v kam´ctcJIÄ¡nSbnepÅ Htc ]mZapÅ {XntImW§Äs¡Ãmw Htc ]c¸fhmsW¶p
aÊnem¡p¶p.
Content Analysis
Term : amdm¯ ]c¸fhv
Facts : c−v kam´ctcJIÄ¡nSbnepÅ Htc ]mZapÅ {XntImW§Äs¡Ãmw Htc ]c¸fhmsW¶p
aÊnem¡p¶p.
Concept : c−v kam´ctcJIÄ¡nSbnepÅ Htc ]mZapÅ {XntImW§Äs¡Ãmw Htc ]c¸fhmsW¶v
Bibw.
Principle : c−v kam´ctcJIÄ¡nSbnepÅ Htc ]mZapÅ {XntImW§Äs¡Ãmw Htc ]c¸fhmWv.

2. Process : c−v kam´ctcJIÄ¡nSbnepÅ Htc ]mZapÅ {XntImW§Äs¡Ãmw Htc ]c¸fhmsW¶p
Is−¯p¶ {]{Inb
Learning Out comes:
1. Remembering information related to the above mentioned facts and concepts.
2. Develops understanding in finding the above facts and concepts.
3. Applying the information in similar situations.
4. Analysing the information to explore understanding and relationships.
5. Creating new ideas related to the above concepts.
6. Justifying the above concepts.
7. Develops skill in finding the above facts and concepts.
Pre-requisites : NXpc¯nsâ ]c¸fhv, {XntImW¯nsâ ]c¸fhv
Teaching- Learning Resources : Bibw hyàam¡p¶ NmÀ«v
Bibw hyàam¡p¶ ssÉUpIÄ

3. Classroom Interaction Preparation Pupil Responses
Preparation :
A[ym]nI ImÀUn sh«nsbSp¯ Nn{Xw
ImWn¡p¶p.
NphsSbpÅ Nn{X¯n {XntImW¯nsâbpw
NXpc¯nsâbpw ]c¸fhpIÄ X½nepÅ _Ôw
F´mWv ?
APB F¶ {XntImW¯np amäap−mbmepw CXp
icnbmIptam ?
Development
A[ym]nI BB bn Hcp Nn{Xw hcbv¡p¶p.

4. {XntImW¯nsâ ]c¸fhnp ta ]dª hmZw
icnbmIptam ?
P bn n¶v A B bnte¡v ew_w hcbv¡p¶p

5. APB bpsS ]c¸fhv = ½ x AB x PQ
= ½ x AB x AD
AXmbXv, Ct¸mgpw {XntImW¯nsâ ]c¸fhv
NXpc¯nsâ ]c¸fhnsâ ]IpXn Xs¶bmWv.
CXn n¶pw c−v kam´ctcJIÄ¡nSbnepÅ
Htc ]mZapÅ {XntImW§Äs¡Ãmw Htc
]c¸fhmWv.
XpSÀ¶v Bibw hyàam¡p¶ NmÀ«v {]ZÀin¸n¡p¶p.

6. c−v kam´c tcJIÄ¡nSbnse {XntImW§Ä.

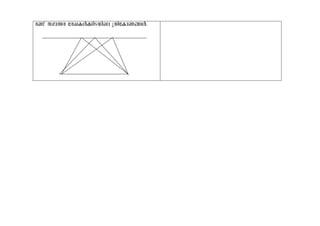
7. c−p kam´c tcJIÄ¡nSbnepÅ Htc ]mZapÅ
{XntImW§Äs¡Ãmw Htc ]c¸fhmWv.
Ip«nIÄ NmÀ«v hmbn¨v Bibw ZrUam¡p¶p.
Application :
Nn{X¯n PQR F¶ {XntImW¯nsâ AtX
]c¸fhpÅ Hcp {XntImWw P bnse tIm¬ a«ambn
hcbv¡mtam ?

8. R eqsS PQ hnv kam´cambn Hcp hc hc¨v
AXnse Hcp _nμp X Dw Bbn PQ tbmPn¸n¨mepw
PQR sâ AtX ]c¸fhpÅ Hcp {XntImWw PQX
In«pw.
F¶m ChnsS asäcp n_ÔIqSn ]men¡Ww
P bnse tIm¬ a«hpamIWw. At¸mÄ aq¶mas¯
ioÀjw P bn¡qSnbpÅ PQ hnsâ
ew_¯nepamIWw.

9. Review : c−p kam´c tcJIÄ¡nSbnepÅ Htc ]mZapÅ {XntIW§fpsS {]tXyIXsb´mWv ?
Follow Up Activity : Nn{X¯n ABC F¶ {XntImW¯nsâ AtX ]c¸fhpÅ Hcp {XntImWw A
tIm¬ a«ambn hcbv¡mtam ?