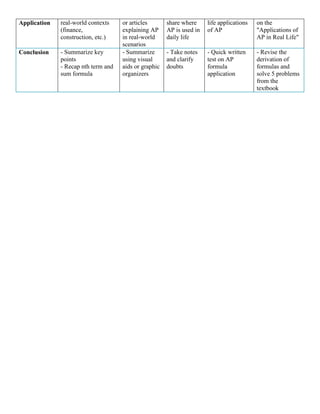
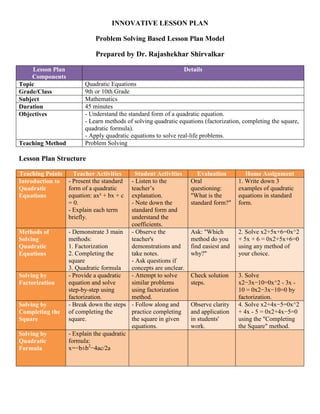
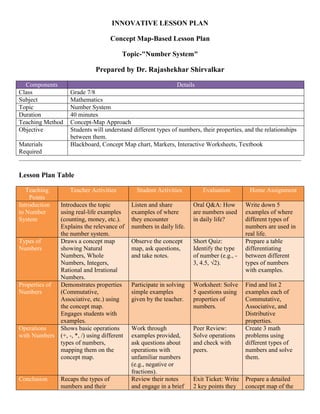
The document details three innovative lesson plans in mathematics focusing on Arithmetic Progression, Quadratic Equations, and Number Systems for grades 7-10. Each plan includes learning objectives, teaching methods, activities, and evaluation components, encouraging real-life application and group collaboration. The plans emphasize understanding mathematical concepts through interactive demonstrations, problem-solving methods, and concept maps.

1. INNOVATIVE LESSON PLAN
Project-based lesson plan model
Topic "Arithmetic Progression"
Prepared by Dr. Rajashekhar Shirvalkar
Title: Arithmetic Progression (AP)
Subject: Mathematics
Grade/Level: 9-10
Duration: 3 Class Periods
Topic: Arithmetic Progression
Learning Objectives:
- Understand the concept of Arithmetic Progression (AP)
- Derive the formula for the nth
term and sum of the first n terms
- Apply AP concepts in real-life situations
Project Outline:
 Title: Understanding and Applying Arithmetic Progression
 Goal: Students work in groups to identify real-life examples of AP and create a presentation
explaining the scenario, deriving the nthn^{th}nth term, and calculating the sum of terms.
 Expected Outcome: Presentations or posters showcasing AP's role in everyday contexts.
Stage Teaching Points Teacher
Activities
Student
Activities
Evaluation Home
Assignment
Introduction - Definition and
examples of
Arithmetic
Progression
- Introduce the
concept of AP
through a
storytelling or
real-life
scenario
- Listen and
participate in
the
discussion
- Oral
questioning to
check initial
understanding
- Find 5
examples of APs
in daily life
situations (e.g.,
savings plan,
seating
arrangement,
etc.)
Development - General form of an
AP: a,a+d,a+2d,…
nth term:
an=a+(n−1)d
a_n = a + (n - 1)
- Derive the
general form
and nth
term
formula using
number
patterns
- Participate
in formula
derivation
and practice
using
examples
- Ask students to
find the 5th or
10th term of a
given AP
- Calculate the nth
term for different
AP sequences
and show the
working
Group
Activity
- Sum of first n terms:
Sn=n/2×[2a+(n−1)d]
- Guide a
group project:
Calculate the
sum of the first
10 terms of a
chosen AP
scenario (e.g.,
daily savings)
- Collaborate
to create a
problem
statement and
solve the AP
scenario
- Evaluate group
presentations
based on
accuracy,
teamwork, and
problem-solving
approach
- Create a small
project on AP:
Compare costs
saved using an
AP sequence
over time for a
hypothetical
budget
Real-Life - Identifying AP in - Show videos - Identify and - Quiz on real- - Create a poster

2. Application real-world contexts
(finance,
construction, etc.)
or articles
explaining AP
in real-world
scenarios
share where
AP is used in
daily life
life applications
of AP
on the
"Applications of
AP in Real Life"
Conclusion - Summarize key
points
- Recap nth term and
sum formula
- Summarize
using visual
aids or graphic
organizers
- Take notes
and clarify
doubts
- Quick written
test on AP
formula
application
- Revise the
derivation of
formulas and
solve 5 problems
from the
textbook

3. INNOVATIVE LESSON PLAN
Problem Solving Based Lesson Plan Model
Prepared by Dr. Rajashekhar Shirvalkar
Lesson Plan
Components
Details
Topic Quadratic Equations
Grade/Class 9th or 10th Grade
Subject Mathematics
Duration 45 minutes
Objectives - Understand the standard form of a quadratic equation.
- Learn methods of solving quadratic equations (factorization, completing the square,
quadratic formula).
- Apply quadratic equations to solve real-life problems.
Teaching Method Problem Solving
Lesson Plan Structure
Teaching Points Teacher Activities Student Activities Evaluation Home Assignment
Introduction to
Quadratic
Equations
- Present the standard
form of a quadratic
equation: ax² + bx + c
= 0.
- Explain each term
briefly.
- Listen to the
teacher’s
explanation.
- Note down the
standard form and
understand the
coefficients.
Oral
questioning:
"What is the
standard form?"
1. Write down 3
examples of quadratic
equations in standard
form.
Methods of
Solving
Quadratic
Equations
- Demonstrate 3 main
methods:
1. Factorization
2. Completing the
square
3. Quadratic formula
- Observe the
teacher's
demonstrations and
take notes.
- Ask questions if
concepts are unclear.
Ask: "Which
method do you
find easiest and
why?"
2. Solve x2+5x+6=0x^2
+ 5x + 6 = 0x2+5x+6=0
using any method of
your choice.
Solving by
Factorization
- Provide a quadratic
equation and solve
step-by-step using
factorization.
- Attempt to solve
similar problems
using factorization
method.
Check solution
steps.
3. Solve
x2−3x−10=0x^2 - 3x -
10 = 0x2−3x−10=0 by
factorization.
Solving by
Completing the
Square
- Break down the steps
of completing the
square.
- Follow along and
practice completing
the square in given
equations.
Observe clarity
and application
in students'
work.
4. Solve x2+4x−5=0x^2
+ 4x - 5 = 0x2+4x−5=0
using the "Completing
the Square" method.
Solving by
Quadratic
Formula
- Explain the quadratic
formula:
x=−b±b2
−4ac/2a

4. INNOVATIVE LESSON PLAN
Concept Map-Based Lesson Plan
Topic-"Number System"
Prepared by Dr. Rajashekhar Shirvalkar
Components Details
Class Grade 7/8
Subject Mathematics
Topic Number System
Duration 40 minutes
Teaching Method Concept-Map Approach
Objective Students will understand different types of numbers, their properties, and the relationships
between them.
Materials
Required
Blackboard, Concept Map chart, Markers, Interactive Worksheets, Textbook
Lesson Plan Table
Teaching
Points
Teacher Activities Student Activities Evaluation Home Assignment
Introduction
to Number
System
Introduces the topic
using real-life examples
(counting, money, etc.).
Explains the relevance of
the number system.
Listen and share
examples of where
they encounter
numbers in daily life.
Oral Q&A: How
are numbers used
in daily life?
Write down 5
examples of where
different types of
numbers are used in
real life.
Types of
Numbers
Draws a concept map
showing Natural
Numbers, Whole
Numbers, Integers,
Rational and Irrational
Numbers.
Observe the concept
map, ask questions,
and take notes.
Short Quiz:
Identify the type
of number (e.g., -
3, 4.5, √2).
Prepare a table
differentiating
between different
types of numbers
with examples.
Properties of
Numbers
Demonstrates properties
(Commutative,
Associative, etc.) using
the concept map.
Engages students with
examples.
Participate in solving
simple examples
given by the teacher.
Worksheet: Solve
5 questions using
properties of
numbers.
Find and list 2
examples each of
Commutative,
Associative, and
Distributive
properties.
Operations
with Numbers
Shows basic operations
(+, -, *, /) using different
types of numbers,
mapping them on the
concept map.
Work through
examples provided,
ask questions about
operations with
unfamiliar numbers
(e.g., negative or
fractions).
Peer Review:
Solve operations
and check with
peers.
Create 3 math
problems using
different types of
numbers and solve
them.
Conclusion Recaps the types of
numbers and their
Review their notes
and engage in a brief
Exit Ticket: Write
2 key points they
Prepare a detailed
concept map of the

5. properties using the
concept map as a
summary.
discussion to clarify
doubts.
learned about the
number system
today.
Number System using
definitions and
examples.
Concept Map Diagram
The central node should be "Number System," with branches showing:
 Natural Numbers: {1, 2, 3...}
 Whole Numbers: {0, 1, 2...}
 Integers: {-3, -2, -1, 0, 1, 2...}
 Rational Numbers: {1/2, -4/5...}
 Irrational Numbers: {π, √2...} Each type of number should also connect to properties and basic
operations for visual clarity.