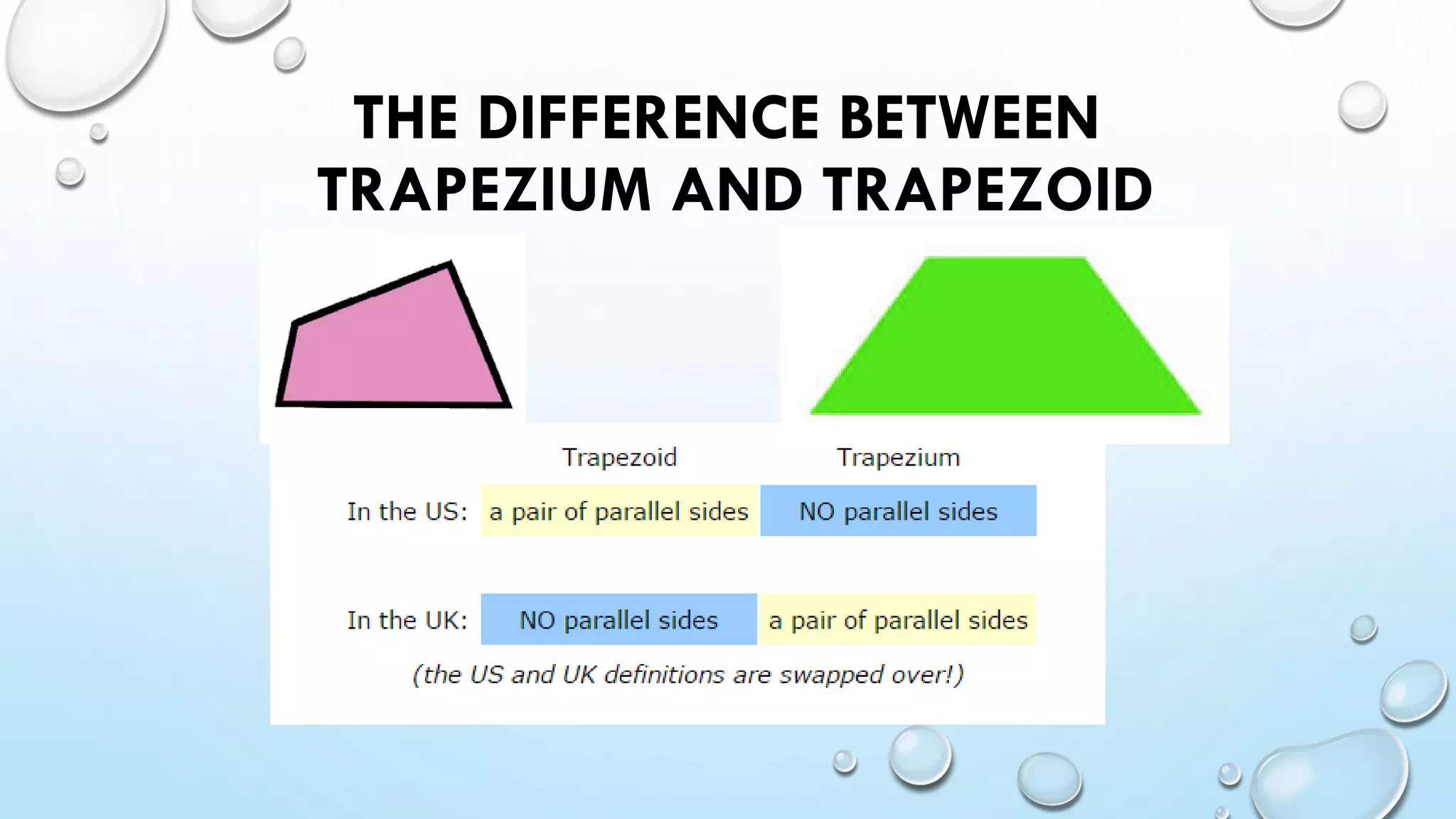
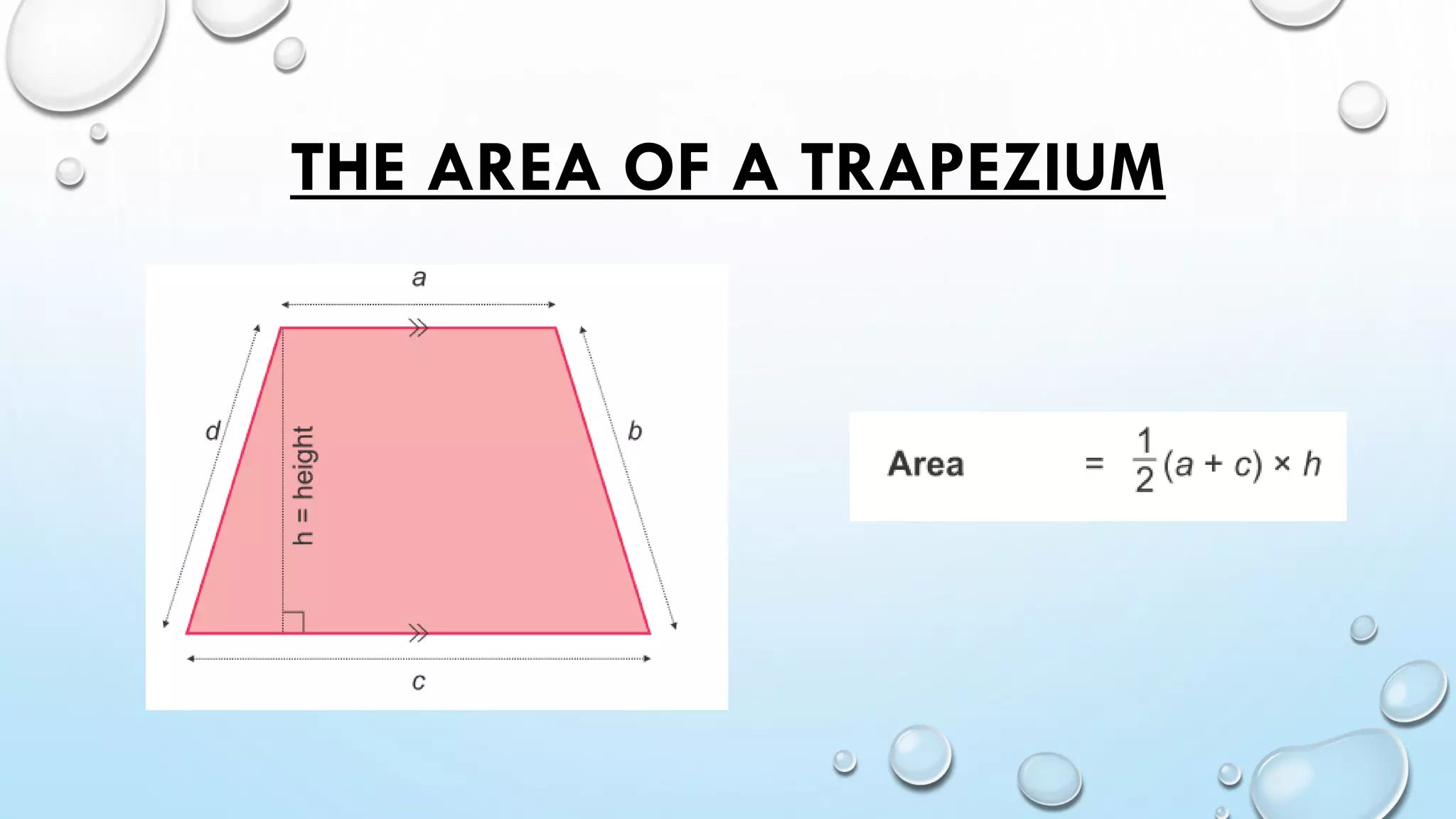
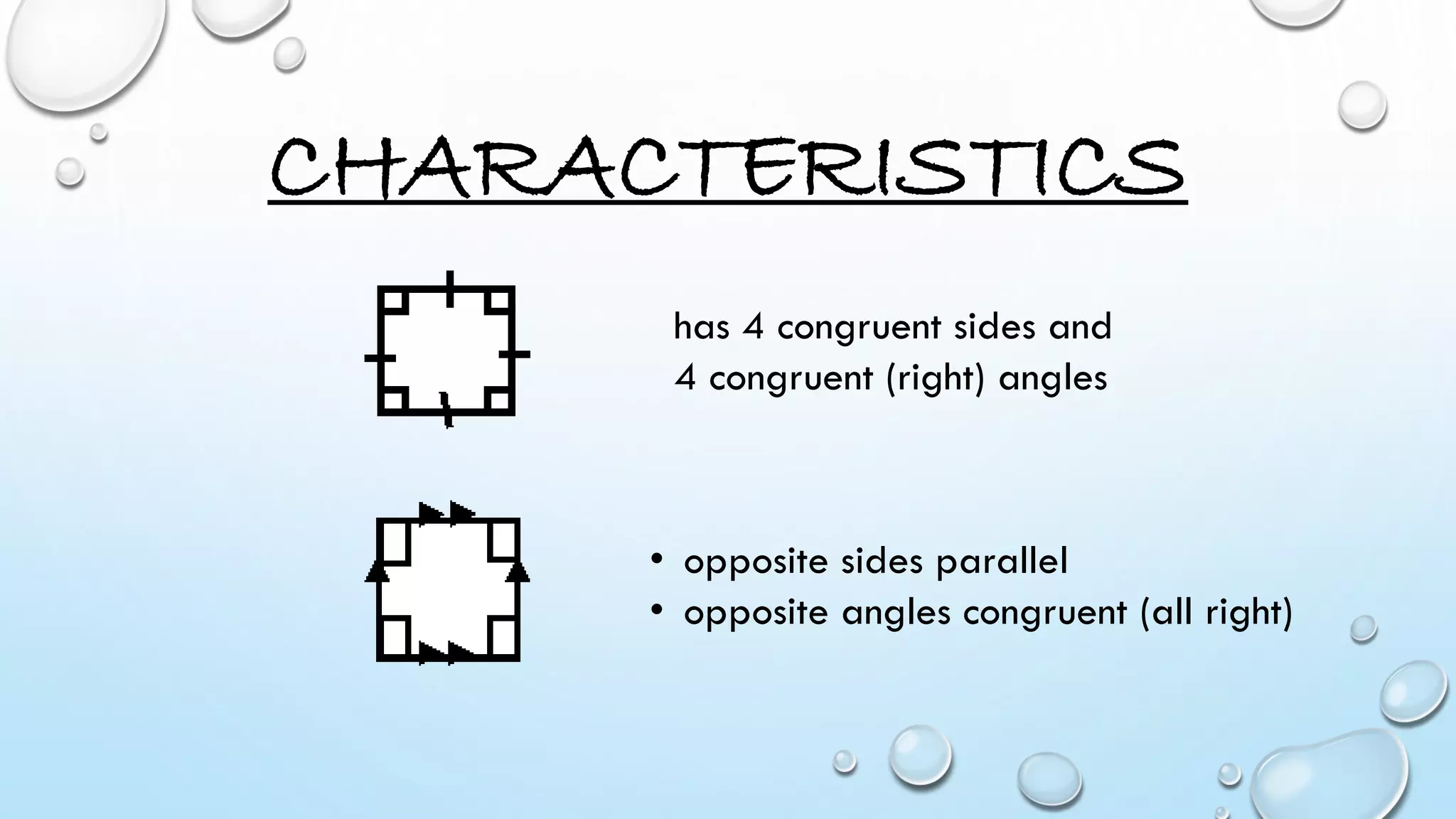
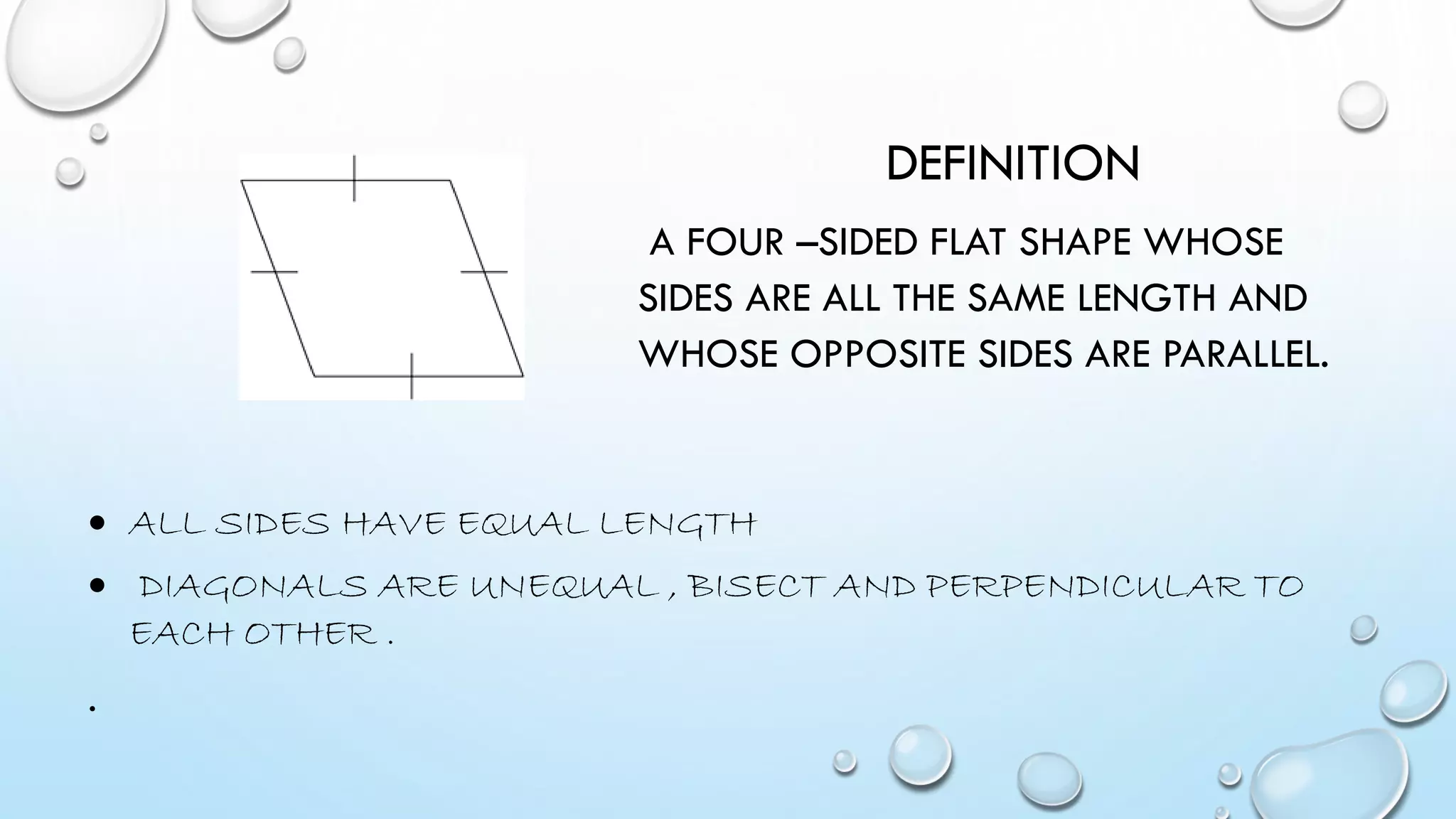
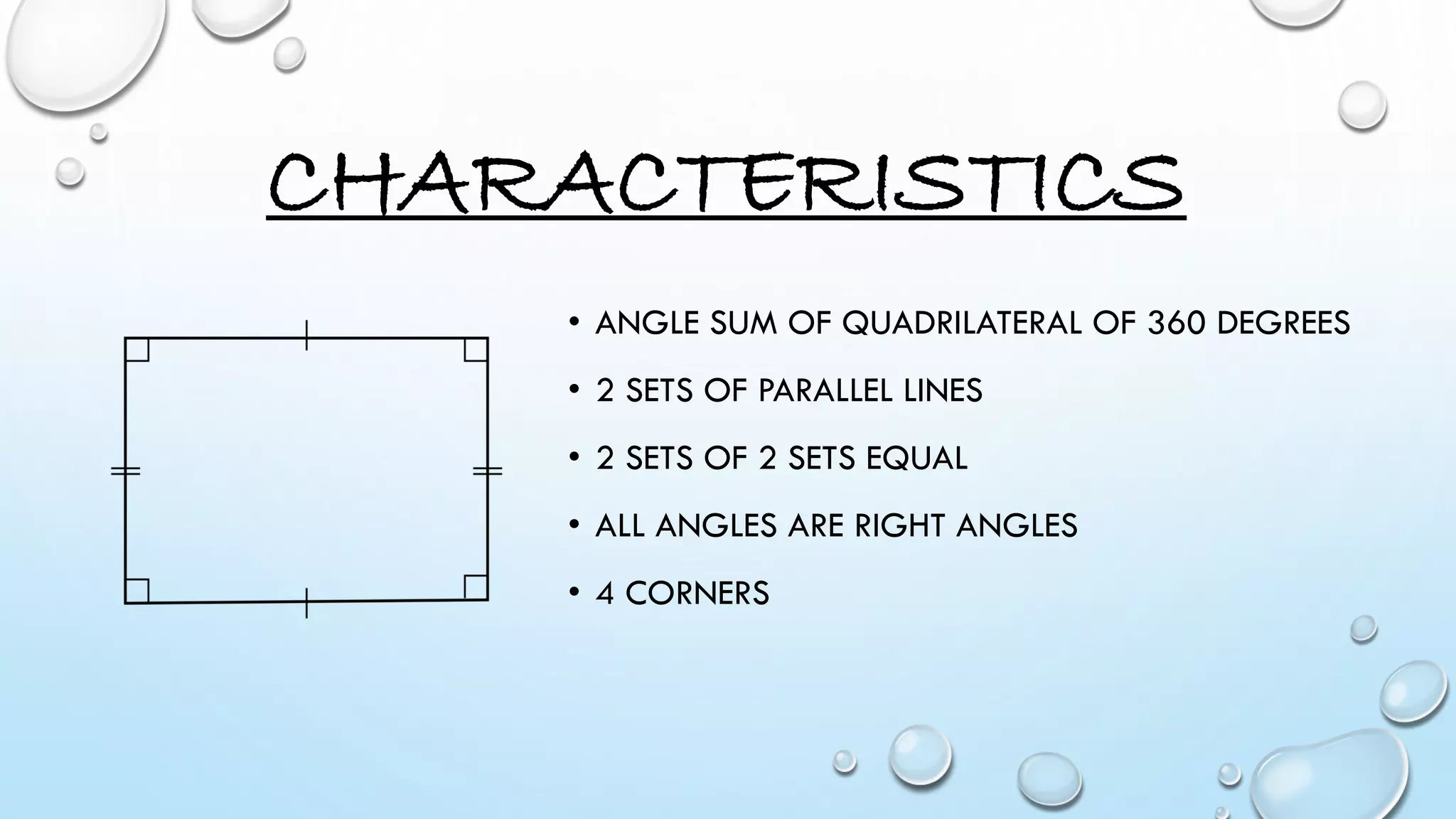
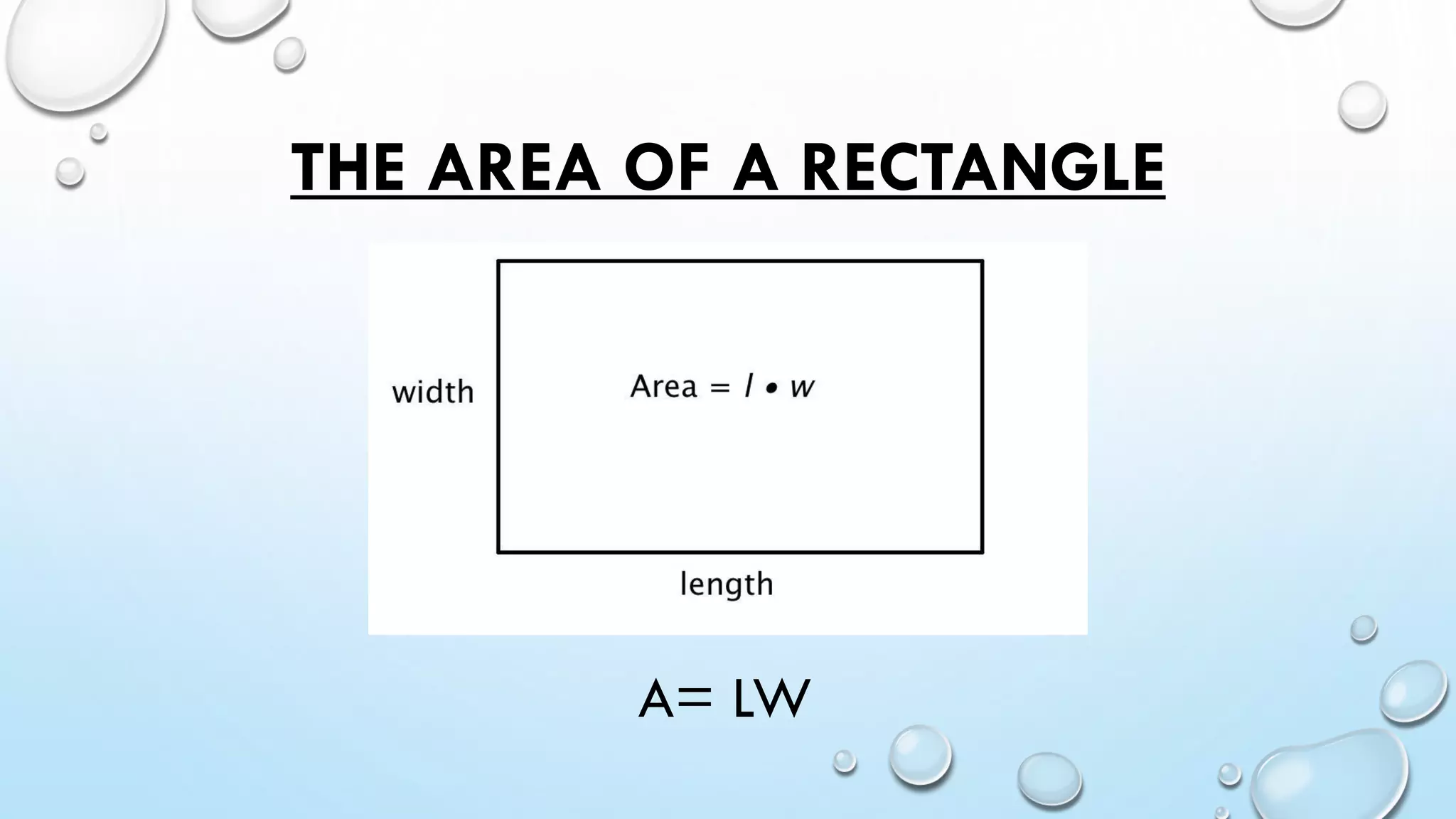
The document defines and provides properties and formulas for various quadrilaterals: - Trapezium has 1 pair of parallel lines and its area is calculated using base times height. - Square has 4 equal sides and 4 right angles and its area is calculated using the square formula. - Rhombus has 4 equal sides and its area can be calculated using base times height, trigonometry, or diagonal methods. - Rectangle has 2 sets of parallel sides and right angles and its area is calculated using length times width. 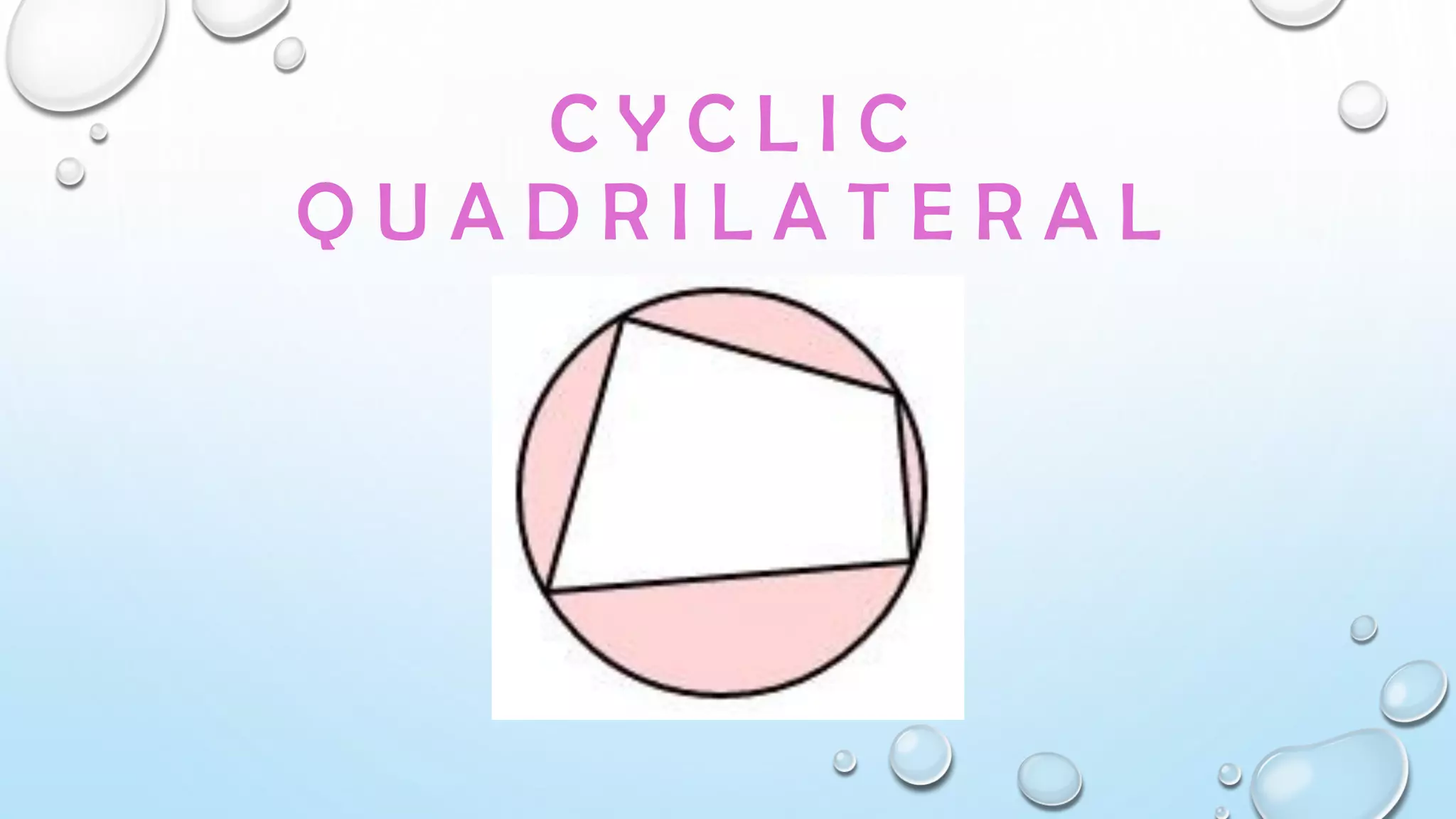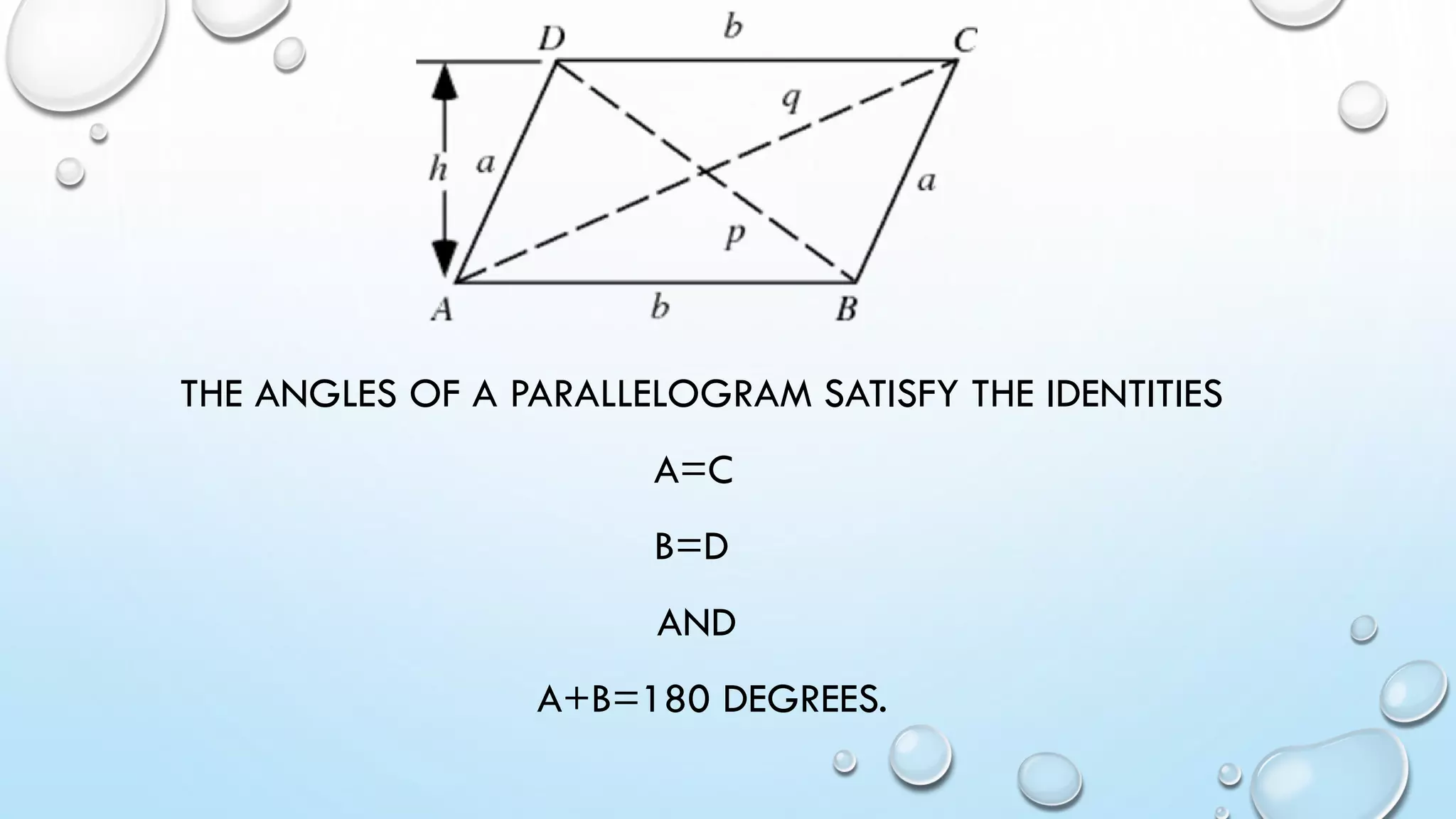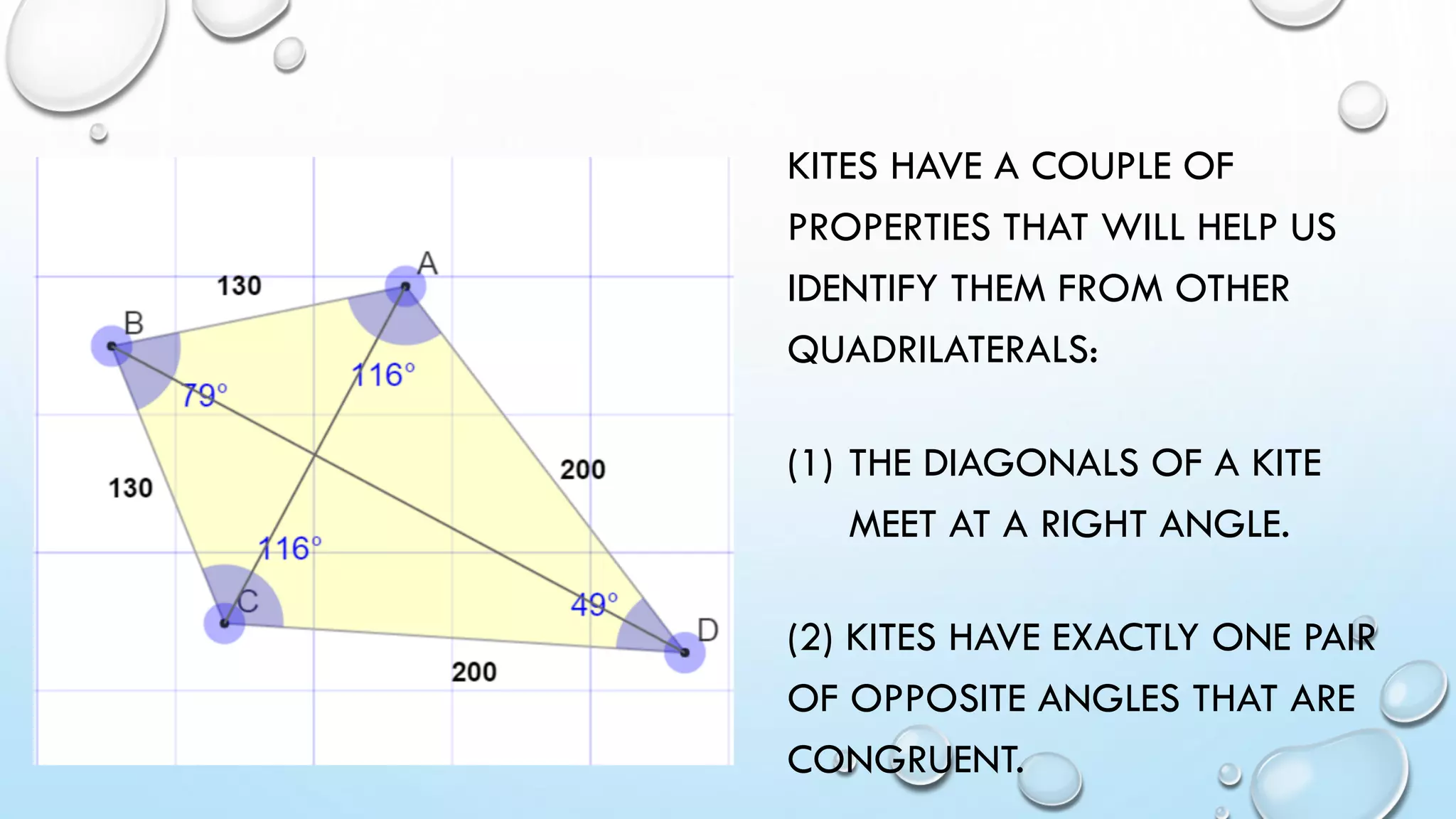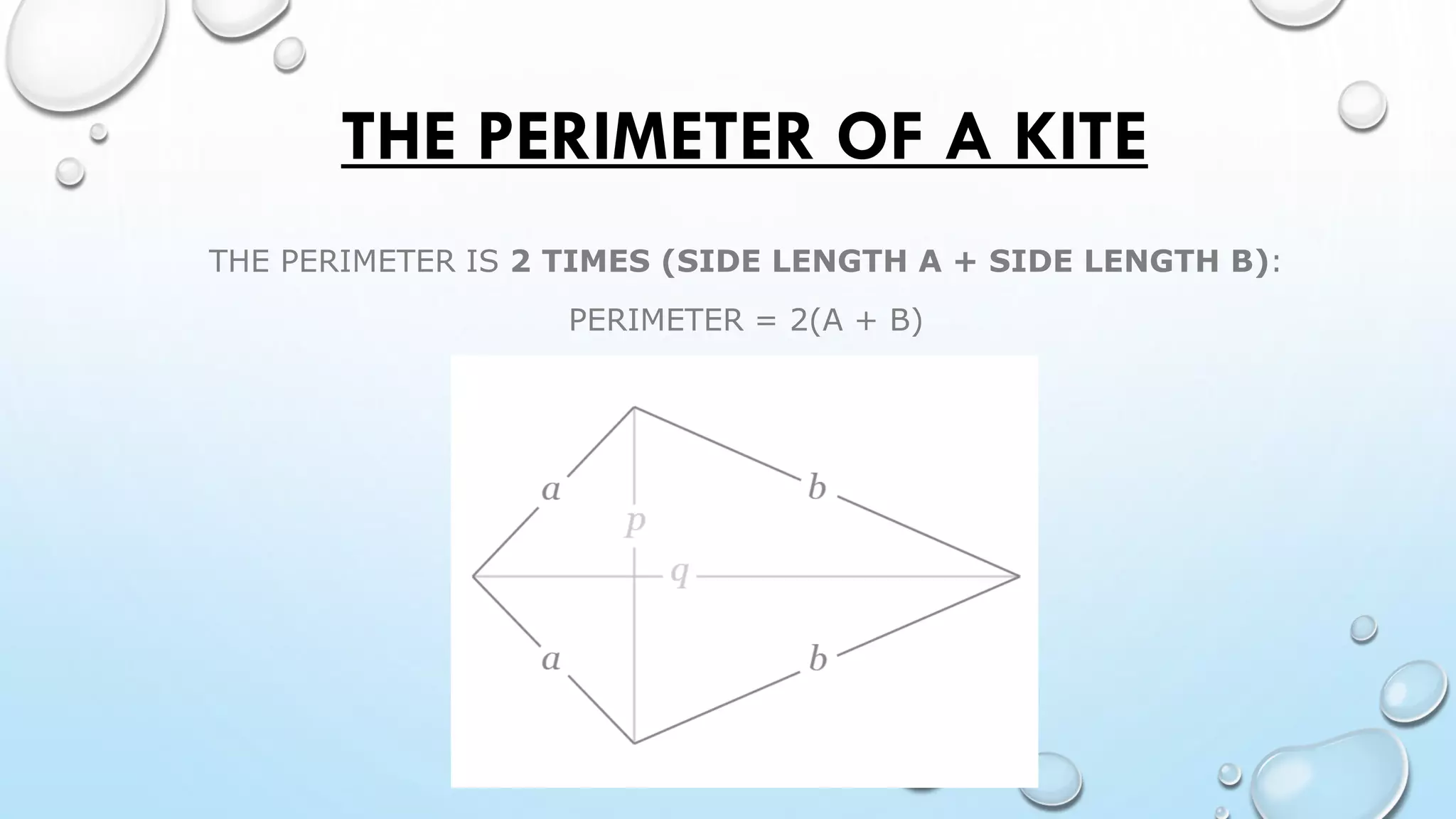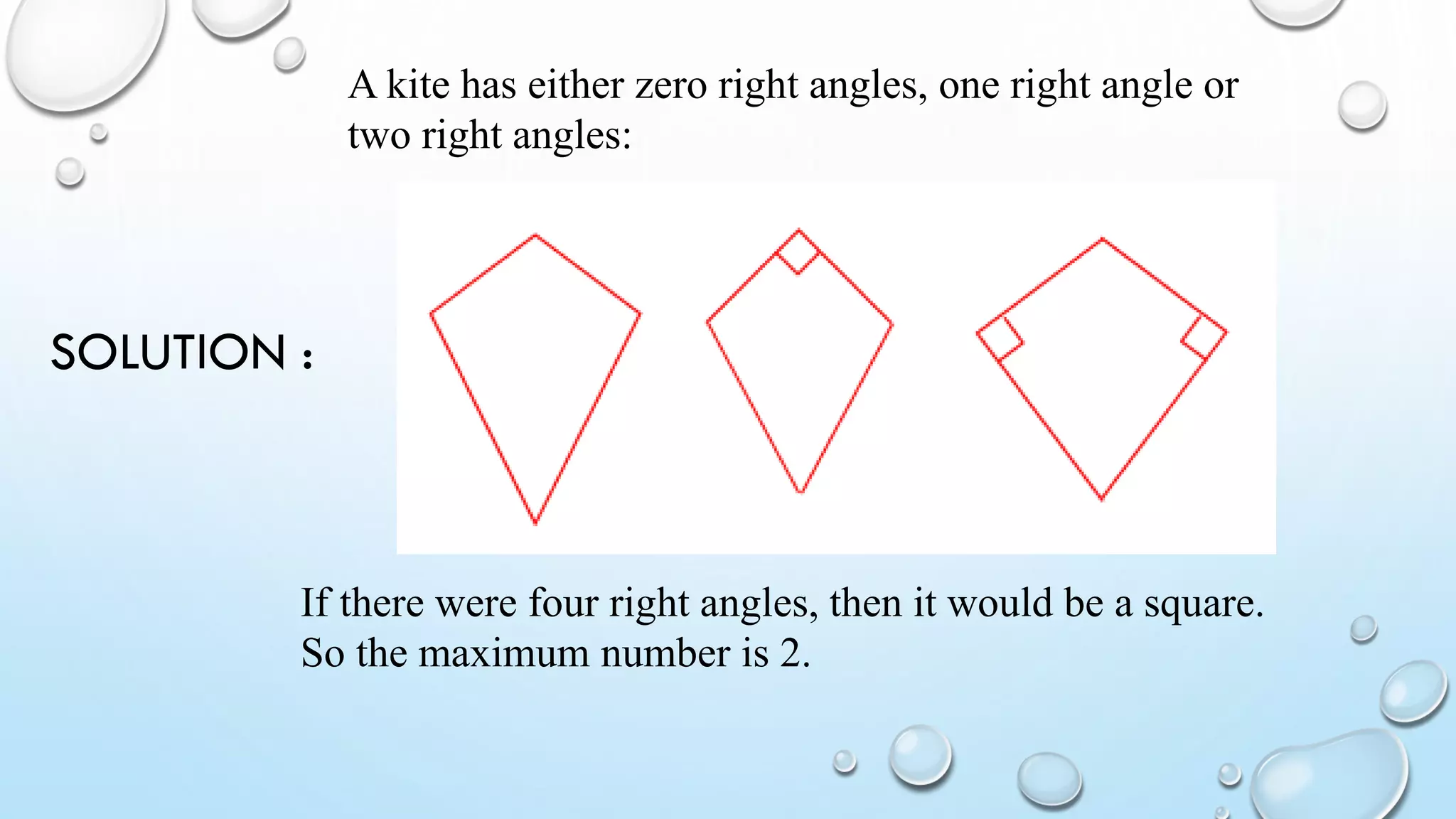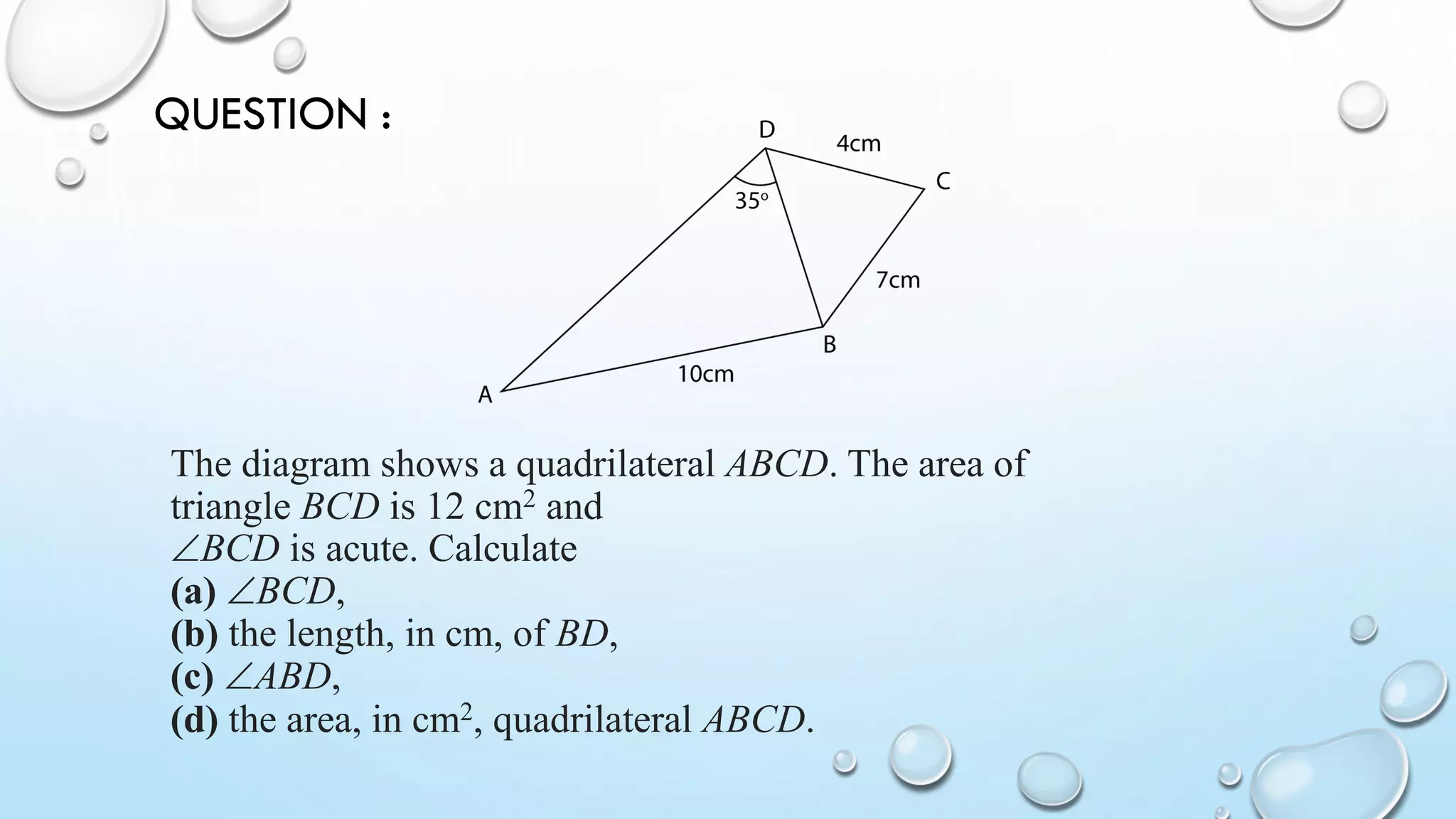The document also discusses cyclic quadrilaterals, irregular quadrilaterals, parallelograms, kites and provides examples of calculating quadrilateral areas and properties.

1. Q.U.A.D.R.I.L.A.T.E.R.A.L

4. T R A P E Z I U M

5. CHARACTERISTICS
• IT HAS 4 SIDES
• IT HAS 1 PAIR OF PARALLEL LINES

6. THE DIFFERENCE BETWEEN
TRAPEZIUM AND TRAPEZOID

7. THE PERIMETER OF A TRAPEZIUM

8. THE AREA OF A TRAPEZIUM

9. S Q U A R E

10. CHARACTERISTICS
has 4 congruent sides and
4 congruent (right) angles
• opposite sides parallel
• opposite angles congruent (all right)

11. diagonals are congruent
AC=BD
diagonals bisect each other
• diagonals bisect opposite
angles
• all bisected angles equal 45º
• diagonals are perpendicular

12. SQUARE FORMULA

13. AREA OF SQUARE FORMULA

14. R H O M B U S

15. DEFINITION
A FOUR –SIDED FLAT SHAPE WHOSE
SIDES ARE ALL THE SAME LENGTH AND
WHOSE OPPOSITE SIDES ARE PARALLEL.
 ALL SIDES HAVE EQUAL LENGTH
 DIAGONALS ARE UNEQUAL , BISECT AND PERPENDICULAR TO
EACH OTHER .
.

16. Area
• Altitude x Base ( the ‘base times height’
method)
• s2 sin A ( the trigonometry method )
• (½) ( d1 x d2 ) / (½) ( p x q ) ( the
diagonals method )
PERIMETER
4S (S+S+S+S)

17. BASE TIMES HEIGHT METHOD
A=bh
where ,
b is the base length
h is the height
A= 5cm x 4cm
= 20cm2

18. TRIGONOMETRY METHOD
A= a² sin A
where
a is the length of a
A is the interior angle
 Rhombus is formed by two equal triangles
Example :
1. The side of a rhombus is 140m and two
opposite angles are 60 degree each. Find the
area.
A = 140² sin 60
= 19600m² x 0.866
= 16973.60m²

19. THE DIAGONALS METHOD
A= (1/2) x (d1 x d2)
Where
d1 is the length of diagonal
d2 is the length of another diagonal
Example :
1. The diagonals of a rhombus are 40m and
20m. Find its area .
A = (1/2) (d1 x d2)
= (1/2) (40m x 20m)
= 400m²

20. R E C T A N G L E

21. CHARACTERISTICS
• ANGLE SUM OF QUADRILATERAL OF 360 DEGREES
• 2 SETS OF PARALLEL LINES
• 2 SETS OF 2 SETS EQUAL
• ALL ANGLES ARE RIGHT ANGLES
• 4 CORNERS

22. A= LW
THE AREA OF A RECTANGLE

23. P = 2L+2W
= 2(L+W)
THE PERIMETER OF A RECTANGLE

24. • DIAGONAL HALF A RECTANGLE
• D= SQUARE ROOT(LENGTH SQUARE+ WIDTH SQUARE)
• PYTHAGORAS THEOREM CAN ALSO BE APPLY TO LOOK FOR THE LENGTH OF THE DIAGONAL
THE DIAGONAL OF A RECTANGLE

25. is
EVERYWHERE !

26. C Y C L I C
Q U A D R I L A T E R A L

27. DEFINITION
CYCLIC QUADRILATERAL IS QUADRILATERAL
WHICH INSCRIBED IN A CIRCLE .

28. PROPERTIES

29. Since
∠ABC+∠ADC=180°,
so ∠ABC= ∠ADE
PROPERTIES

30. AREA OF CYCLIC QUADRILATERAL
where s is the semi-perimeter of quadrilateral
The Brahmagupta’s Formula :

31. I R R E G U L A R
Q U A D R I L A T E R A L

32. • IRREGULAR QUADRILATERAL DOES
NOT HAVE ANY SPECIAL PROPERTIES
• IRREGULAR QUADRILATERAL IS ONE
WHERE THE SIDES ARE UNEQUAL OR
THE ANGLES ARE UNEQUAL OR
BOTH
CHARACTERISTICS

33. P A R A L L E L O G R A M

34. A QUADRILATERAL WITH
OPPOSITE SIDES PARALLEL
(AND THEREFORE OPPOSITE
ANGLES EQUAL)

35. • OPPOSITE SIDES ARE CONGRUENT (AB = DC).
• OPPOSITE ANGELS ARE CONGRUENT (B = D).
• CONSECUTIVE ANGLES ARE SUPPLEMENTARY (A +B = 180°).
• IF ONE ANGLE IS RIGHT, THEN ALL ANGLES ARE RIGHT.
• THE DIAGONALS OF A PARALLELOGRAM BISECT EACH OTHER.
• EACH DIAGONAL OF A PARALLELOGRAM SEPARATES IT INTO TWO CONGRUENT
TRIANGLES. (ABC AND ACD)

36. THE ANGLES OF A PARALLELOGRAM SATISFY THE IDENTITIES
A=C
B=D
AND
A+B=180 DEGREES.

37. A PARALLELOGRAM OF BASE, B AND HEIGHT H HAS AREA
AREA= BXH
THE AREA OF A PARALLELOGRAM

38. K I T E

39. • IT LOOKS LIKE A KITE. IT HAS TWO PAIRS
OF SIDES.
• EACH PAIR IS MADE UP OF ADJACENT
SIDES (THE SIDES THEY MEET) THAT ARE
ALSO EQUAL IN LENGTH.
• THE ANGLES ARE EQUAL WHERE THE
PAIRS MEET.
• DIAGONALS (DASHED LINES) MEET AT A
RIGHT ANGLE, AND ONE OF THE
DIAGONAL BISECTS (CUTS EQUALLY IN
HALF) THE OTHER.​

40. KITES HAVE A COUPLE OF
PROPERTIES THAT WILL HELP US
IDENTIFY THEM FROM OTHER
QUADRILATERALS:
(1) THE DIAGONALS OF A KITE
MEET AT A RIGHT ANGLE.
(2) KITES HAVE EXACTLY ONE PAIR
OF OPPOSITE ANGLES THAT ARE
CONGRUENT.

41. THE PERIMETER IS 2 TIMES (SIDE LENGTH A + SIDE LENGTH B):
PERIMETER = 2(A + B)
THE PERIMETER OF A KITE

42. THE AREA OF A KITE
1ST METHOD: USING THE "DIAGONALS" METHOD.
The Area is found by multiplying the lengths of the
diagonals and then dividing by 2:
x and y refers to the
length of the diagonals.

43. 2ND METHOD: USING TRIGONOMETRY.
When you have the lengths of all sides and a measurement of the angle
between a pair of two unequal sides, the area of a standard kite is
written as: Area = a b sin C
a and b refer to length of two
unequal sides.
C refers to the angle between
two different sides.
sin refers to the sine function in
trigonometry.

44. FOR A KITE THAT IS NOT A SQUARE OR A RHOMBUS,
WHAT IS THE MAXIMUM NUMBER OF RIGHT ANGLES IT
COULD HAVE?
QUESTION :
A. 1
B. 2
C. 4

45. SOLUTION :
A kite has either zero right angles, one right angle or
two right angles:
If there were four right angles, then it would be a square.
So the maximum number is 2.

46. QUESTION :
Given that h=8 , determine
the perimeter and the area of
the trapezium.

47. QUESTION :
Given area of the square is
324.
Find the perimeter and the
diagonal length of the
square.

48. QUESTION :
Find the area of the rhombus
having each side equal to 17 cm
and one of its diagonals equal to
16 cm.

49. ABCD is a rhombus in which AB = BC = CD
= DA = 17 cm
AC = 16 cm
Therefore, AO = 8 cm
In ∆ AOD,
AD2 = AO2 + OD2
⇒ 172 = 82 + OD2
⇒ 289 = 64 + OD2
⇒ 225 = OD2
⇒ OD = 15
Therefore, BD = 2 OD
= 2 × 15
= 30 cm
Now, area of rhombus
= 1/2 × d1 × d2
= 1/2 × 16 × 30
= 240 cm2
SOLUTION :

50. QUESTION
THE DIAGONAL D OF A RECTANGLE HAS A
LENGTH OF 100 FEET AND ITS LENGTH Y IS
TWICE ITS WIDTH X (SEE FIGURE BELOW).
FIND ITS AREA.

51. EXAMPLE :
Find the area of a cyclic quadrilateral whose sides
are 36m , 77m , 75m , 40m.
Solution : Given a=36m, b=77m , c=75m , d=40m
s = (36+77+75+40)/2
= ( 228)/2
=114m
Using Brahmagupta’s Formula :
Area of cyclic quadrilateral =
√(s−a)(s−b)(s−c)(s−d)
A= √(114-36)(114−77)(114−75)(114-40)
= √ (78)(37)(39)(74)
= √ 8328996
= 2886 m2

52. The diagram shows a quadrilateral ABCD. The area of
triangle BCD is 12 cm2 and
BCD is acute. Calculate
(a) BCD,
(b) the length, in cm, of BD,
(c) ABD,
(d) the area, in cm2, quadrilateral ABCD.
QUESTION :

53. SOLUTION :
(b) Using cosine rule,
BD2 = BC2 + CD2 – 2 (7)(4) cos 59o
BD2 = 72 + 42 – 2 (7)(4) cos 59o
BD2 = 65 – 28.84
BD2 = 36.16
BD= √36.16
BD = 6.013 cm
(c) Using sine rule,
(d) Area of quadrilateral ABCD
= Area of triangle ABD + Area of
triangle BCD
= ½ (AB)(BD) sin B + 12 cm
= ½ (10) (6.013) sin 124.82 + 12
= 24.68 + 12
= 36.68 cm²
(a) Given area of triangle BCD = 12 cm2
½ (BC)(CD) sin C = 12
½ (7) (4) sin C = 12
14 sin C = 12
sin C = 12/14 = 0.8571
C = 59o
BCD = 59o

54. A PARALLELOGRAM HAS AN AREA
OF 28 SQUARE CENTIMETRES. IF
ITS BASE IS 4 CENTIMETRES,
CALCULATE THE HEIGHT OF THE
PARALLELOGRAM.
QUESTION :