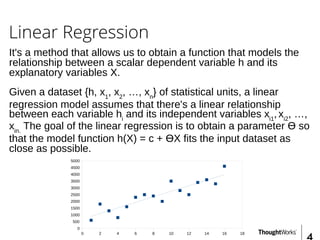
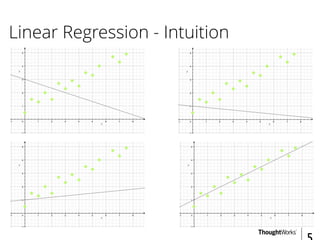
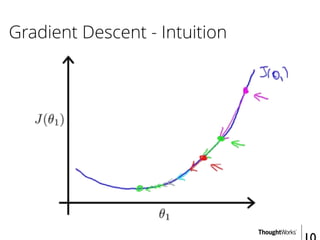
This document provides an overview of recommender systems including background information, implementation details, and a demonstration. It discusses machine learning applications like unsupervised learning, linear regression, and gradient descent algorithms. It covers content-based filtering using known product features and collaborative filtering to identify unknown product features. Examples are given on using linear regression and gradient descent to make predictions for skills data and handle unknown values.

1. Recommender
Systems
João Paulo L. F. Dias da Silva
Oct 2014

2. Background
(5 min)
Implementation
(5 min)
Demonstration
(5 min)
Agenda

3. Background 1. Machine Learning Application
• Unsupervised Learning (No
right answers provided)
• Linear Regression
• Gradient Descent Algorithm
2. Content-based Filtering
• Known product features
3. Collaborative Filtering
• Unknown product features
• Features will be “identified”
by the application

4. Linear Regression
It's a method that allows us to obtain a function that models the
relationship between a scalar dependent variable h and its
explanatory variables X.
Given a dataset {h, x1
, x2
, …, xn
} of statistical units, a linear
regression model assumes that there's a linear relationship
between each variable hi
and its independent variables xi1
, xi2
, …,
xin.
The goal of the linear regression is to obtain a parameter Ɵ so
that the model function h(X) = c + ƟX fits the input dataset as
close as possible.
0 2 4 6 8 10 12 14 16 18
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000

5. Linear Regression - Intuition

6. Linear Regression – Model function
hi
= Ɵ1
xi1
+ … + Ɵm
xim
Stacking all examples we can rewrite the above as:
hi
= xi
T
Ɵ
Where X is a nx1 vector with each element being xi
T
and n is the
number of examples of our dataset.
T denotes the transpose operation.
Let h be a function that represents a model for the ith
example of
our dataset:
h = XƟ
Let Ɵ and xi
be mx1 vectors where m is the number of variables
of our model, so hi
becomes:

7. Linear Regression – Error function
Let h(X) be our hypothesis function (model).
J = (h(X) - Y)2
Let Y be the target values for each example in our dataset.
The squared error function J will be:
Another way of writing the error function is to take into account
the index of each example in our dataset, so that:
m
J = ∑(h(x(i)
) – Y(i)
)2
i=1
The objective of the linear regression is to minimize the error
function J with respect to Ɵ. One way of achieving it is through an
algorithm called Gradient Descent.

8. Gradient Descent Algorithm
Objective:
Find the minimum values for Ɵ1
,...,Ɵn
that minimize the error
function J(Ɵ1
,...,Ɵn
).
Overview:
• Initialize Ɵ1
,...,Ɵn
with some random values.
• Keep changing Ɵ1
,...,Ɵn
to reduce J(Ɵ1
,...,Ɵn
) until we find a
minimum.
Implementation:
Ɵj
:= Ɵj
– α – ∂ J(Ɵ1
,...,Ɵn
)
∂Ɵj

9. Gradient Descent
The partial derivative:
m
Ɵj
:= Ɵj
– α 1 – ∑(h(x(i)
) – y(i)
)x(i)
m i=1 j
An example for Ɵ ∈ ℝ3
:
m
Ɵ0
:= Ɵ0
– α 1 – ∑(h(x(i)
) – y(i)
)x(i)
m i=1 0
m
Ɵ1
:= Ɵ1
– α 1 – ∑(h(x(i)
) – y(i)
)x(i)
m i=1 1
m
Ɵ2
:= Ɵ2
– α 1 – ∑(h(x(i)
) – y(i)
)x(i)
m i=2 2

10. Gradient Descent - Intuition

11. Recommender Systems – Prog. Skills
Skills Ana Beto Carla Daniel
Ruby 5 5 0 0
CSS3 5 ? ? 0
JS ? 4 0 ?
Android 0 0 5 4
iOS 0 0 5 ?
How to predict the values for the unknown skills?

12. Content-based Filtering
Skills
Ana
Ɵ¹
Beto
Ɵ2 ...
X1
(Web)
X2
(Mobile)
Ruby (X1
) 5 5 ... 0.9 0
CSS3 (X2
) 5 ? ... 1.0 0.01
JS (X3
) ? 4 ... 0.99 0
Android (X4
) 0 0 ... 0.1 1.0
iOS (X5
) 0 0 ... 0 0.9
The skills features are known. Just need to solve one Linear Regression per user.

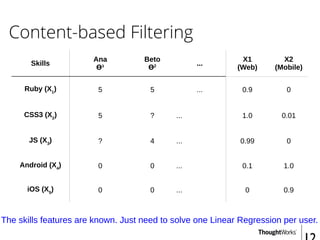
13. Content-based Filtering - Predicting
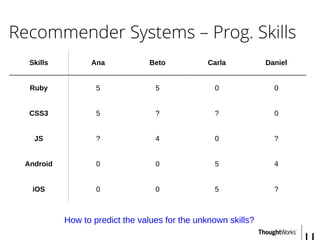
Skills
Ana
Ɵ¹ = [5, 0]
...
X1
(Web)
X2
(Mobile)
Ruby (X1
) 5 ... 0.9 0
CSS3 (X2
) 5 ... 1.0 0.01
JS (X3
) 5 ... 0.99 0
Android (X4
) 0 ... 0.1 1.0
iOS (X5
) 0 ... 0 0.9
Ana(JS) => Ɵ¹ * X3
=> [5, 0] * [0.99, 0] = (5 * 0.99) + (0 * 0) = 5

14. Collaborative Filtering
Skills
Ana
Ɵ¹
Beto
Ɵ2 ...
X1
(?)
X2
(?)
Ruby (X1
) 5 5 ... ? ?
CSS3 (X2
) 5 ? ... ? ?
JS (X3
) ? 4 ... ? ?
Android (X4
) 0 0 ... ? ?
iOS (X5
) 0 0 ... ? ?
How to predict the values for the unknown skills and features?

15. Collaborative Filtering – Feature
Learning
We can't find the Ɵ parameters because we don't have the values
for the features vectors.
So we initialize the Ɵ parameters to random values.
Then we can use the Ɵ parameters to apply linear regression in
order to find the features vectors for each skill.
Then we can use the features vectors to apply linear regression to
improve our Ɵ parameters for each user.
We keep doing that until we reach the optimal values for Ɵ and
the features vectors.

16. Collaborative Filtering – Intuition

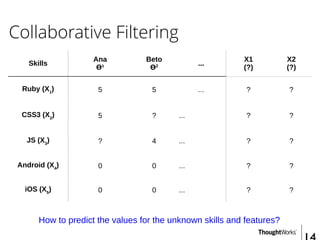
17. Collaborative Filtering - Predicting
Skills
Ana
Ɵ¹ = [5, 0]
... X1 X2
Ruby (X1
) 5 ... 0.9 0
CSS3 (X2
) 5 ... 1.0 0.01
JS (X3
) 5 ... 0.99 0
Android (X4
) 0 ... 0.1 1.0
iOS (X5
) 0 ... 0 0.9
Ana(JS) => Ɵ¹ * X3
=> [5, 0] * [0.99, 0] = (5 * 0.99) + (0 * 0) = 5

18. Implementa
tion
Python for data scraping
Octave for LR/GD matrix calculations
Missing UI
Hardcoded input

19. Demo
Programming
Skills

20. QA & Next Steps