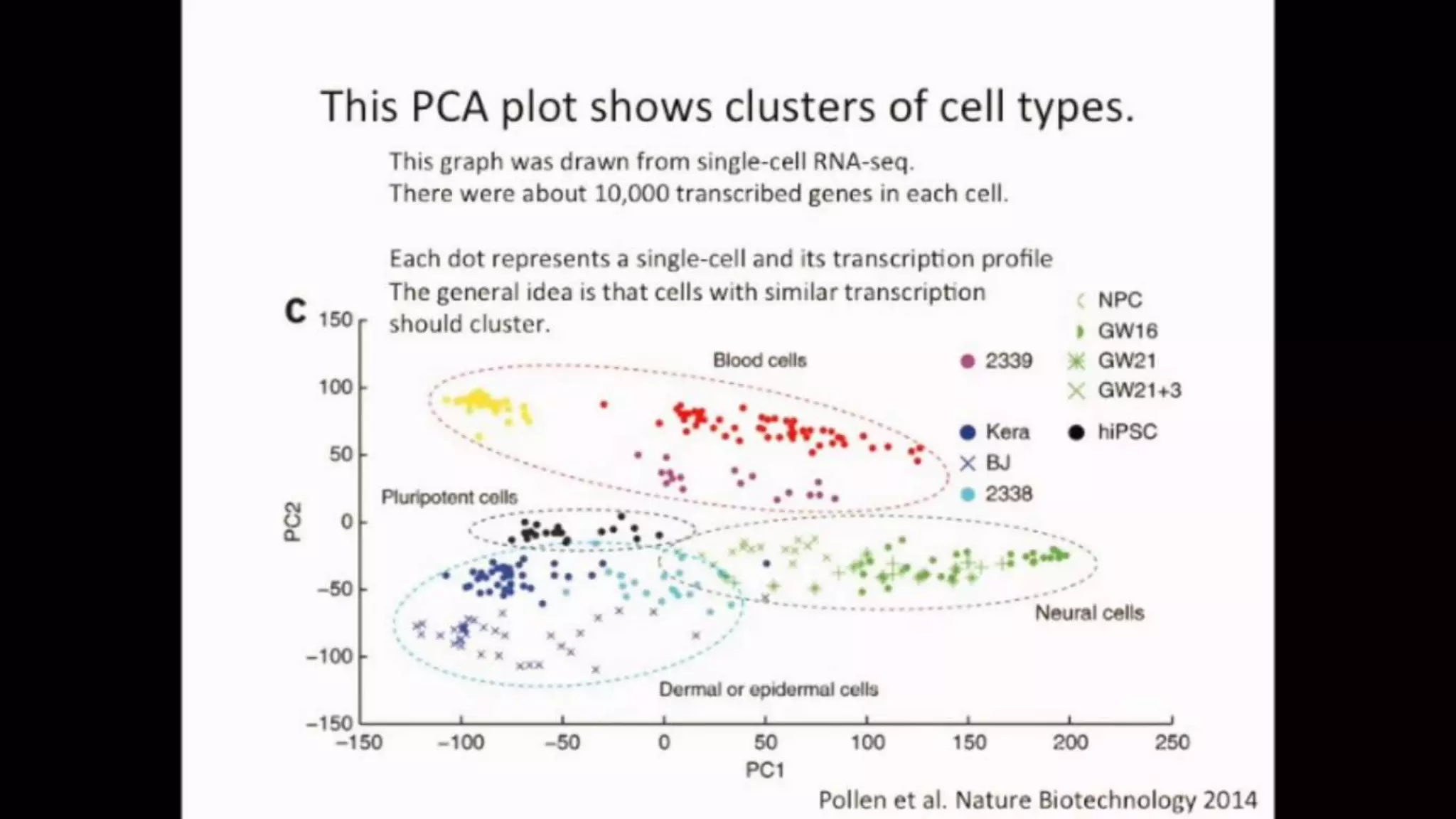
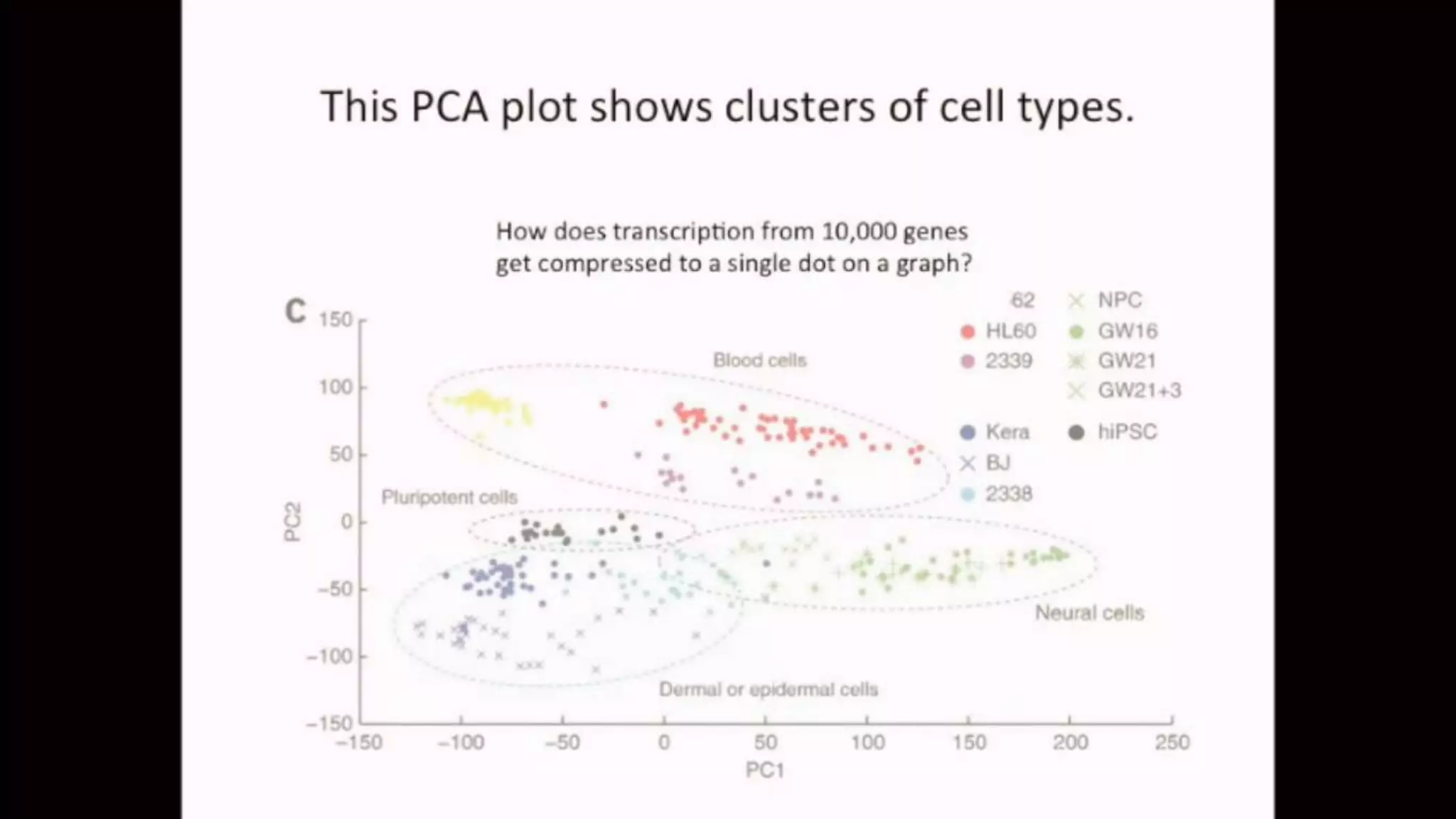
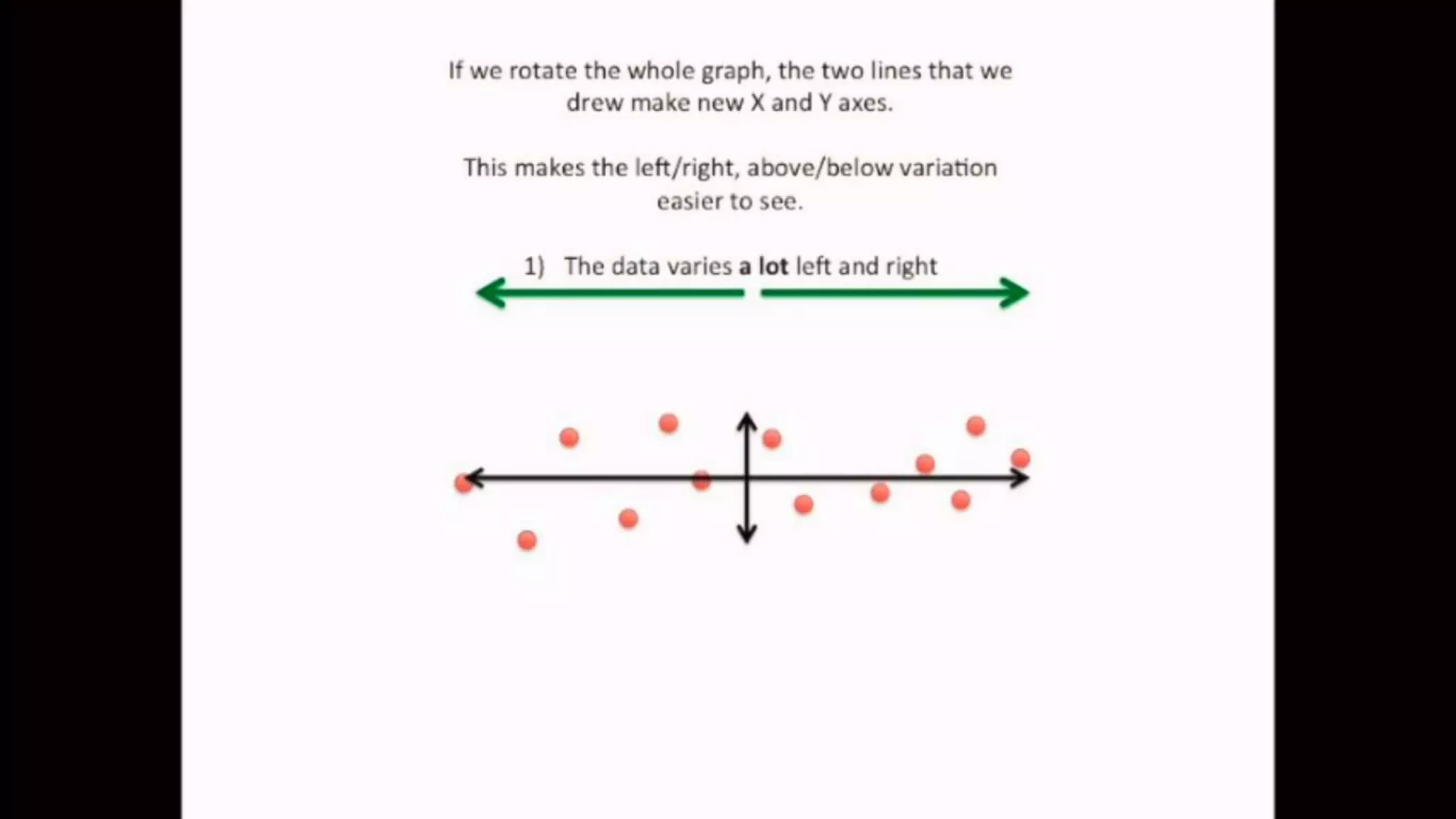
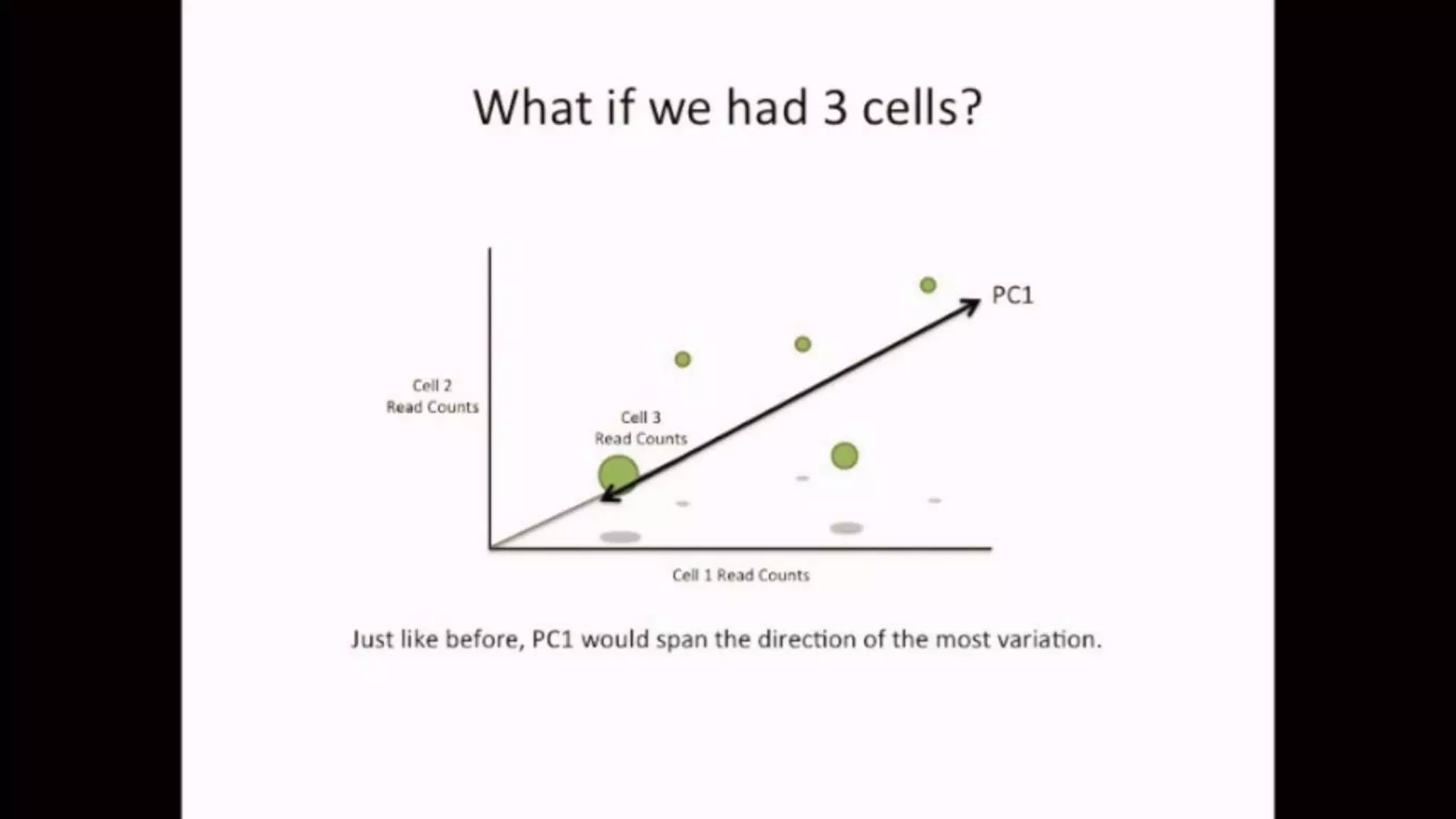
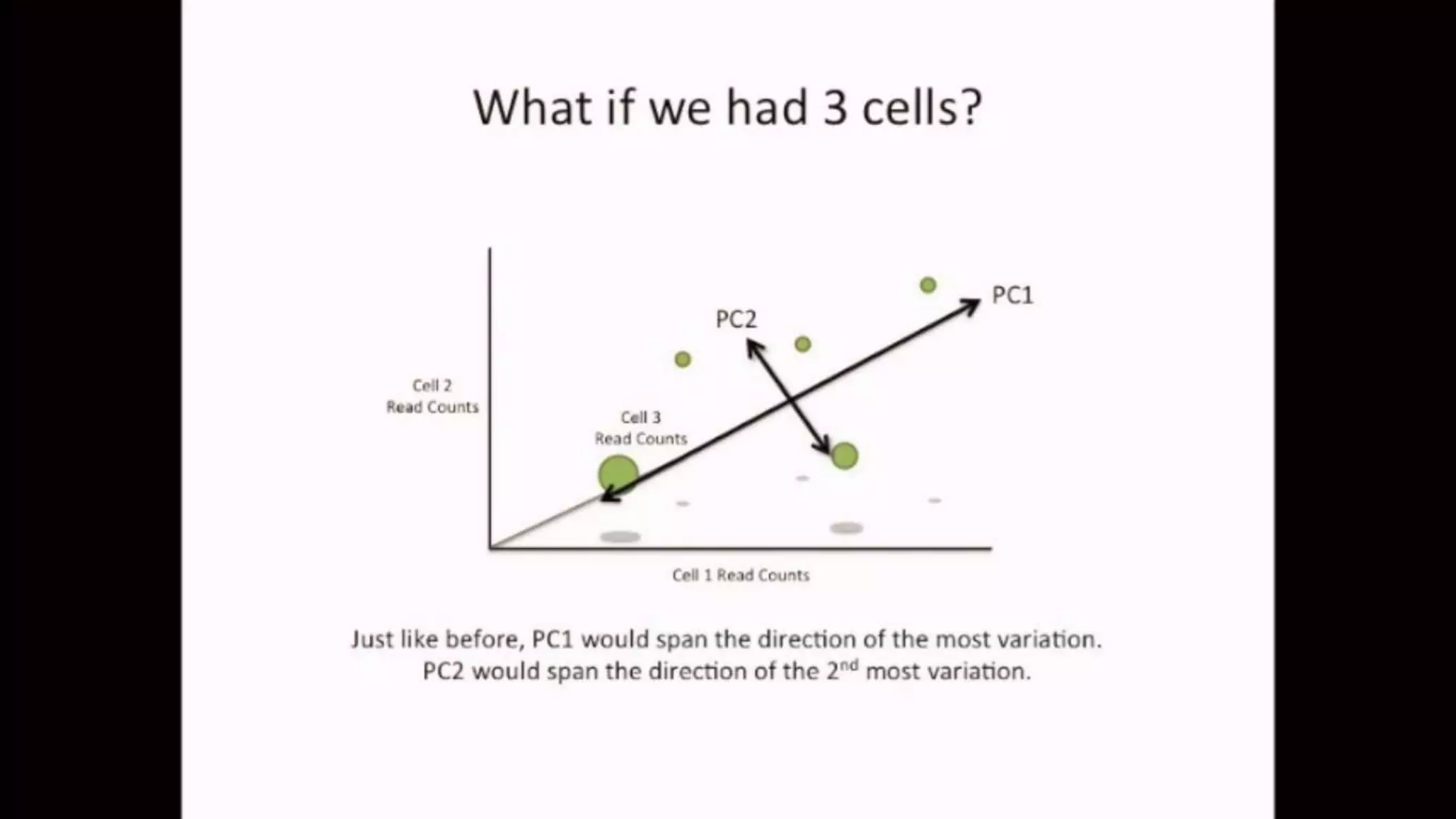
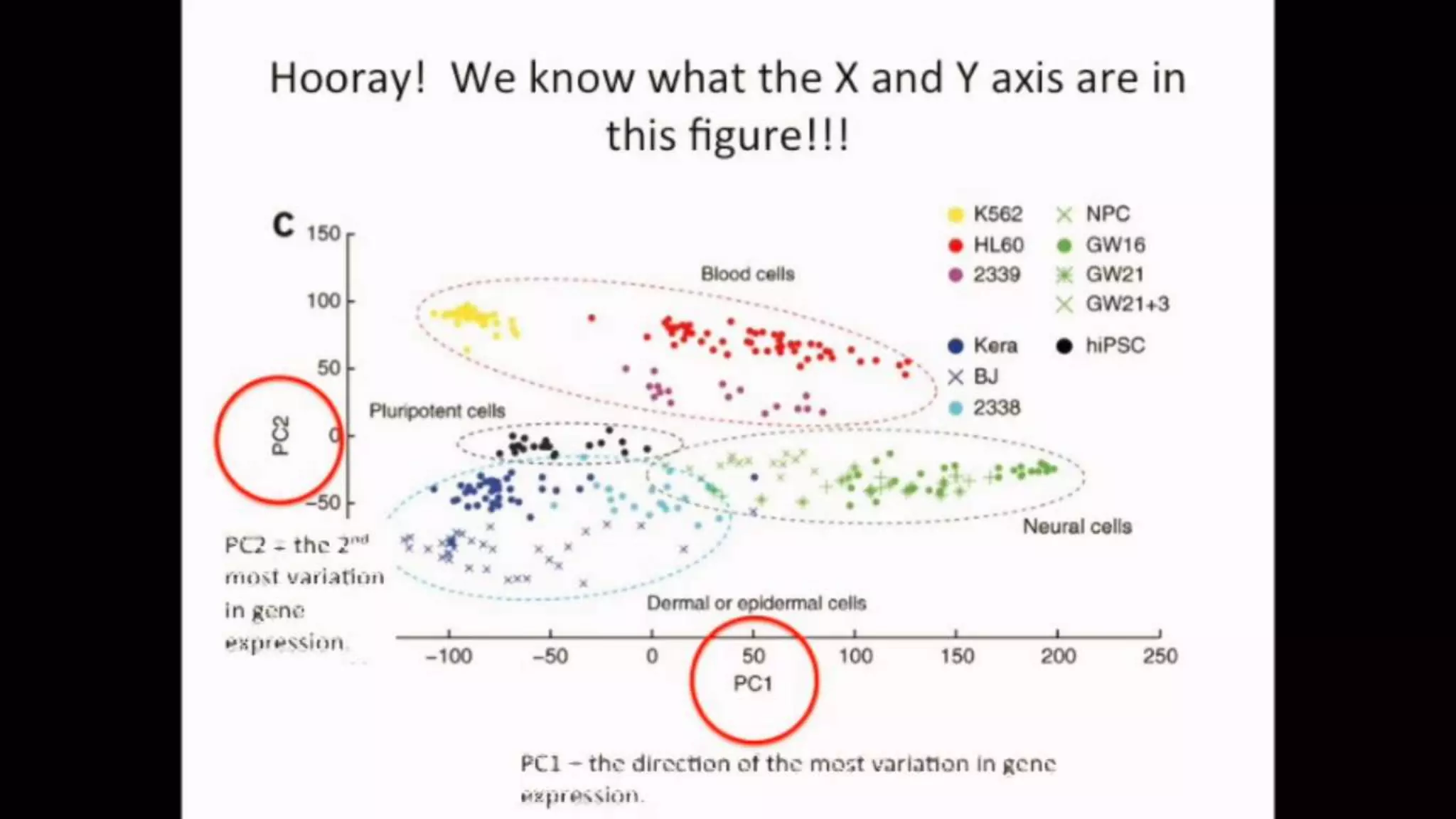
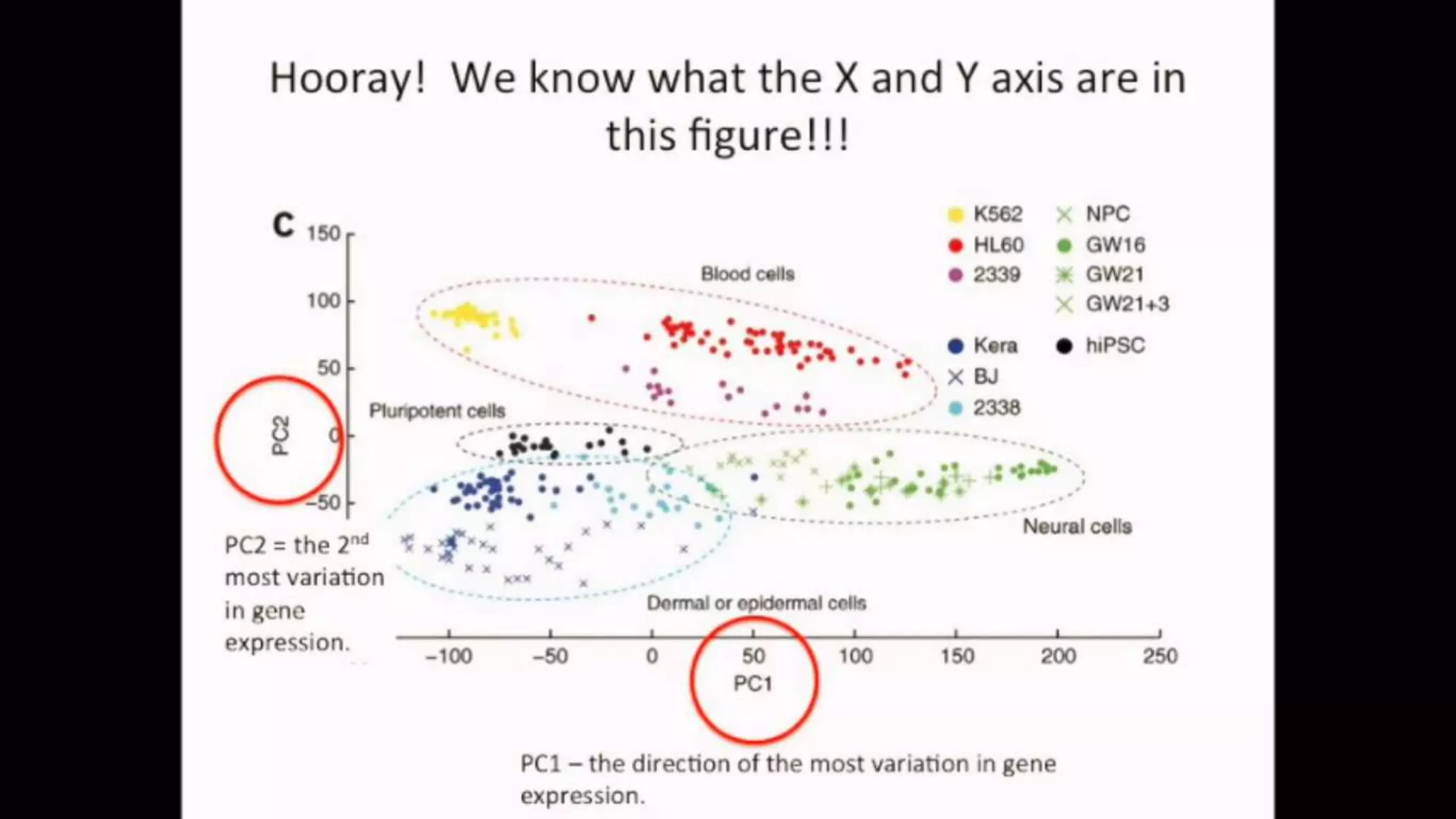
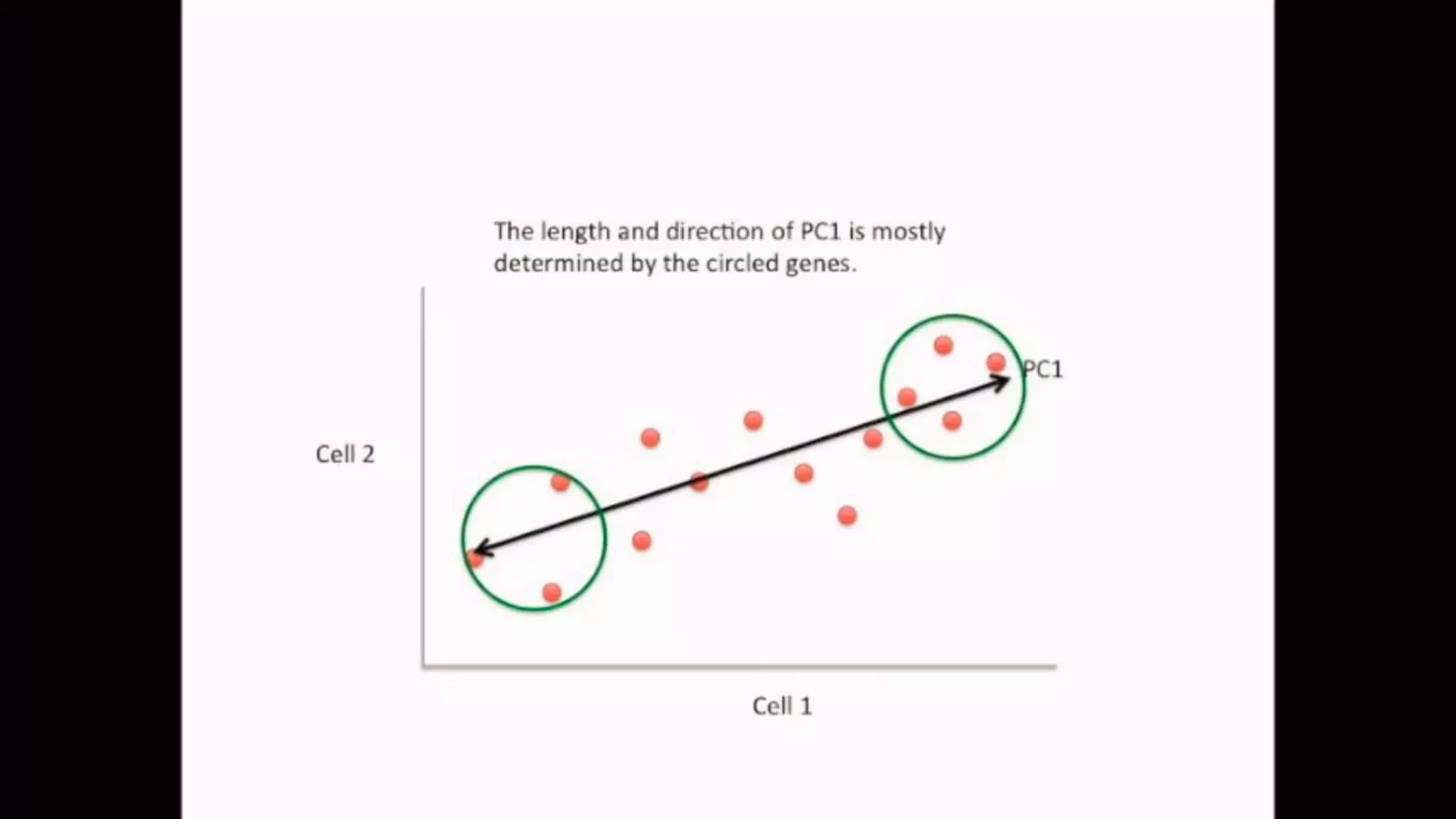
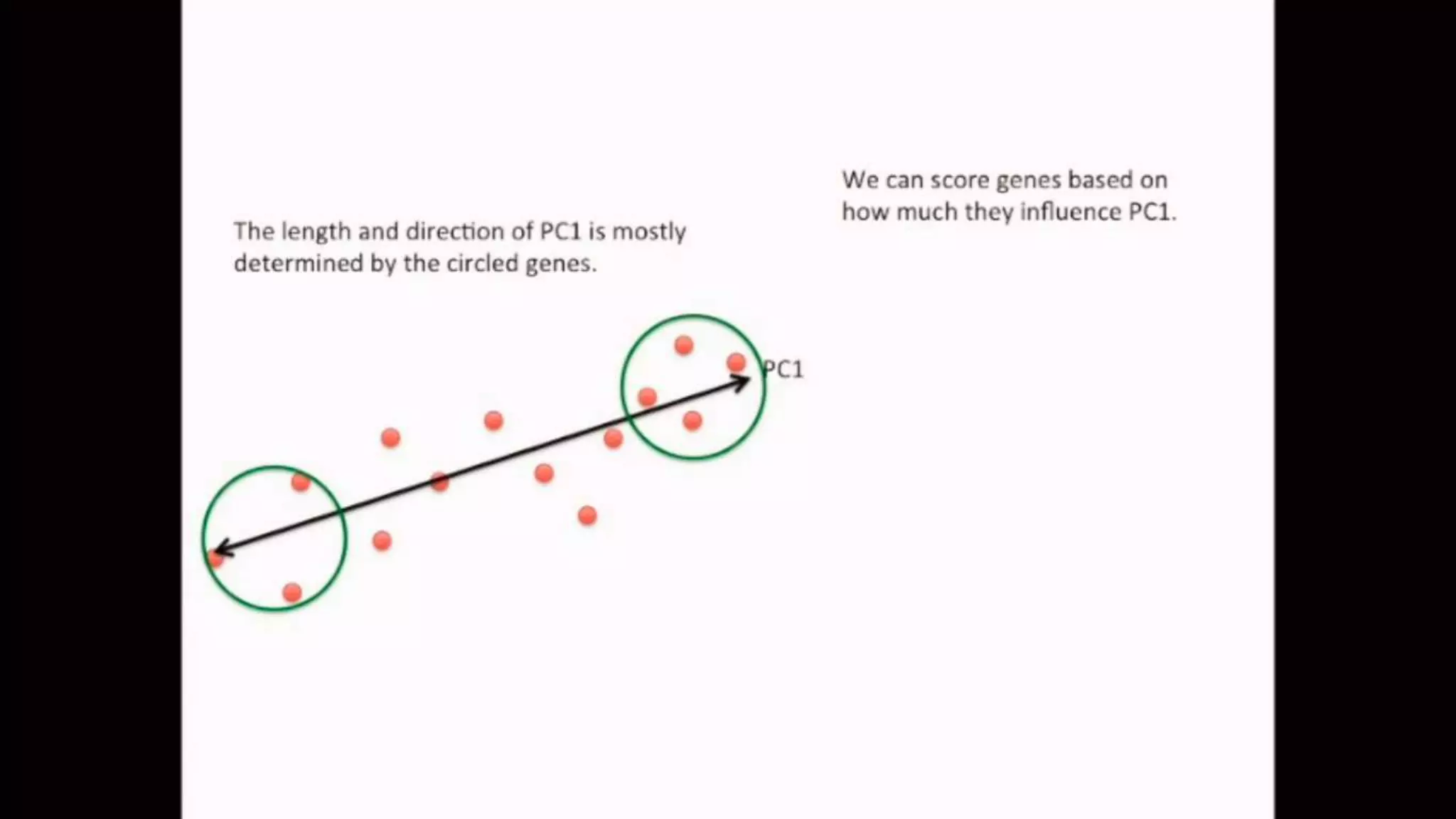
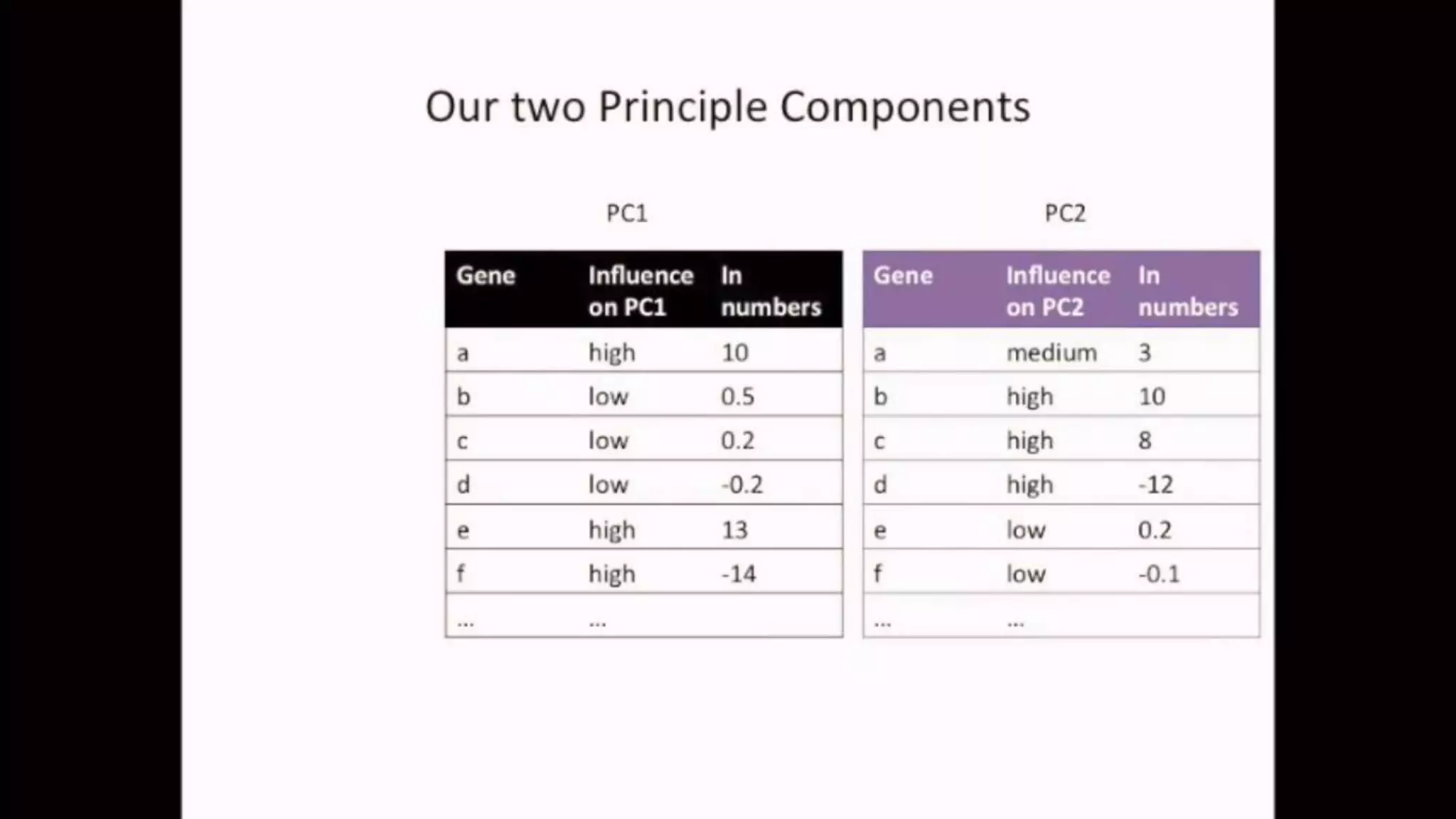
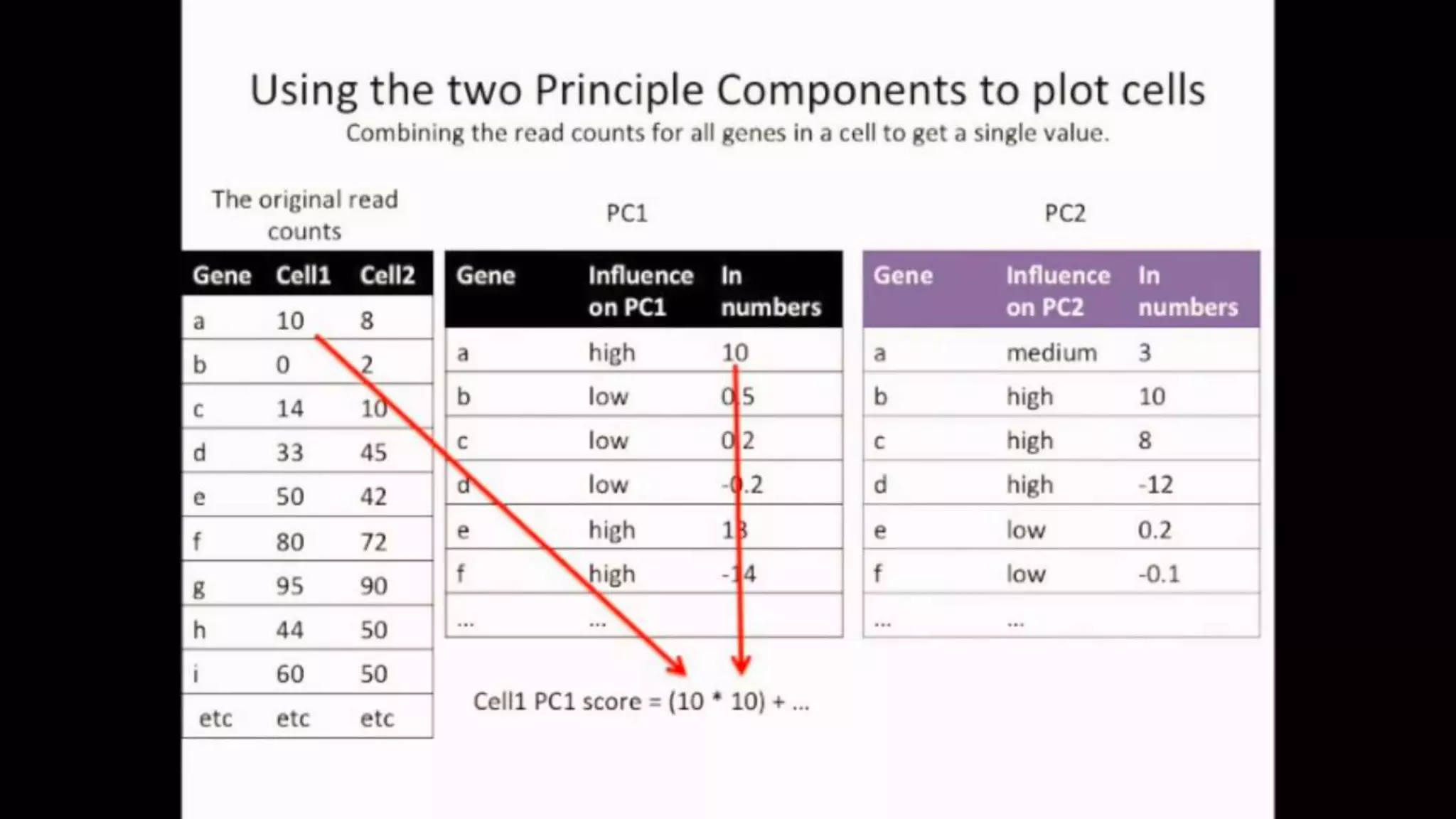
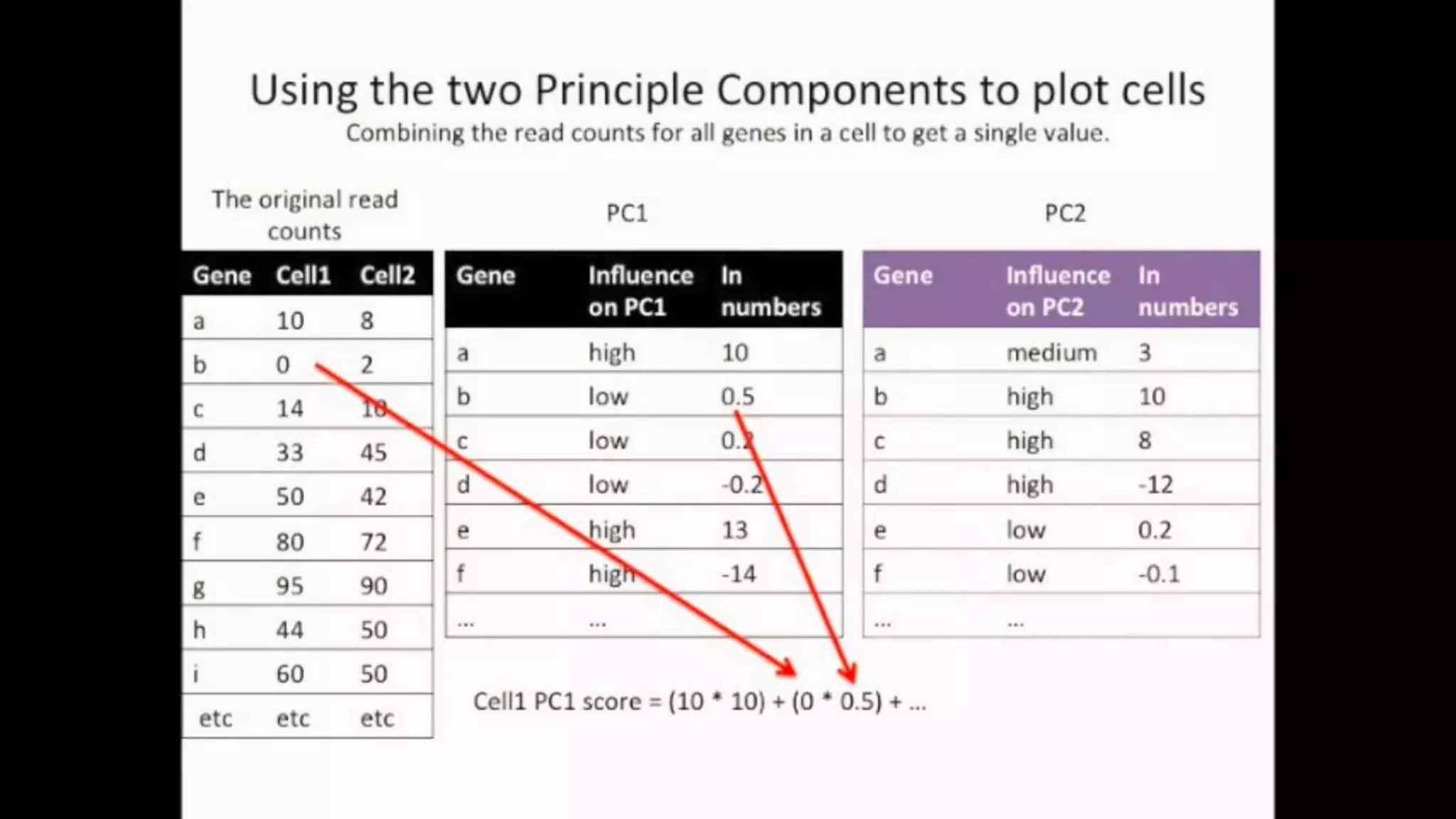
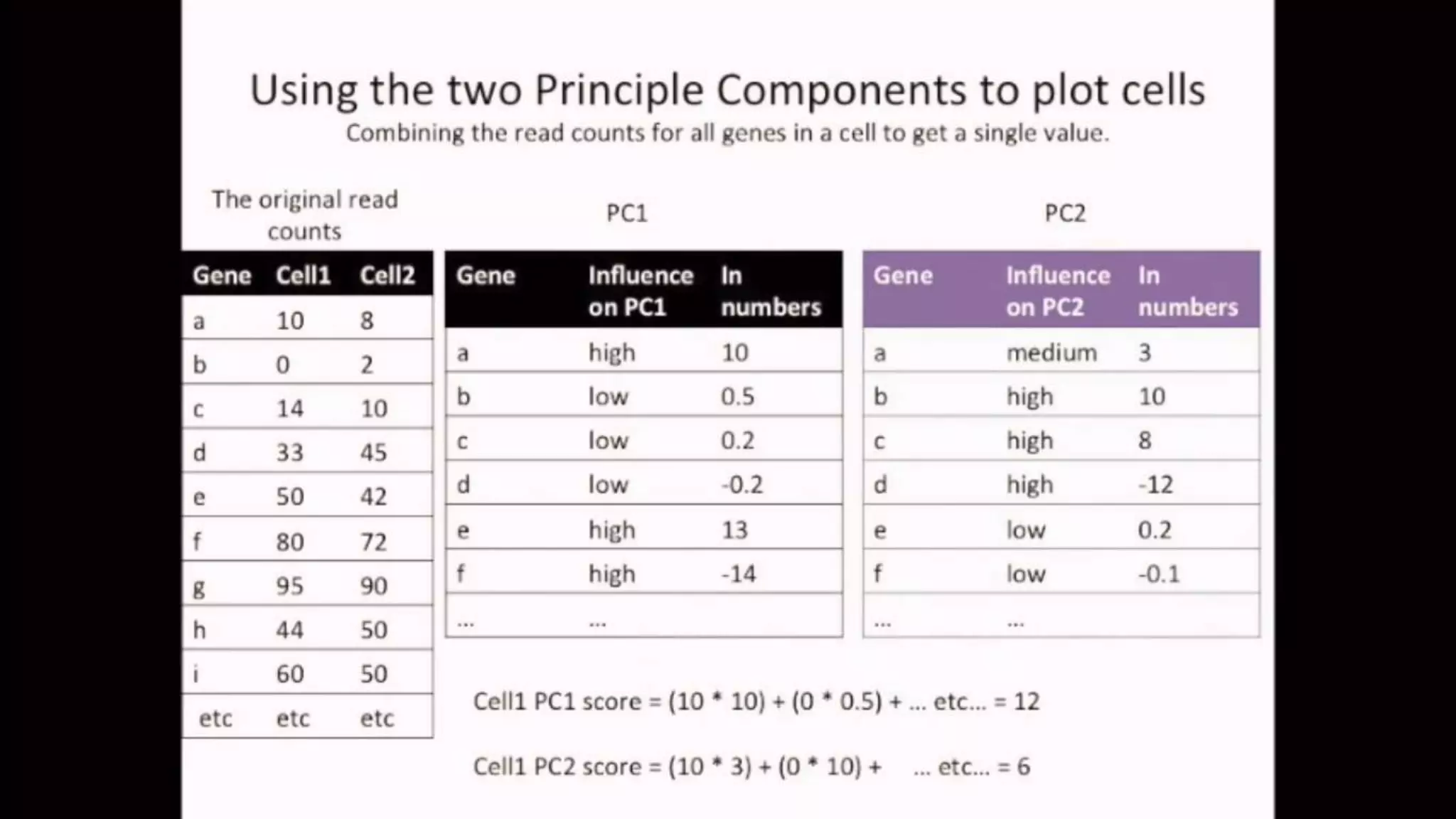
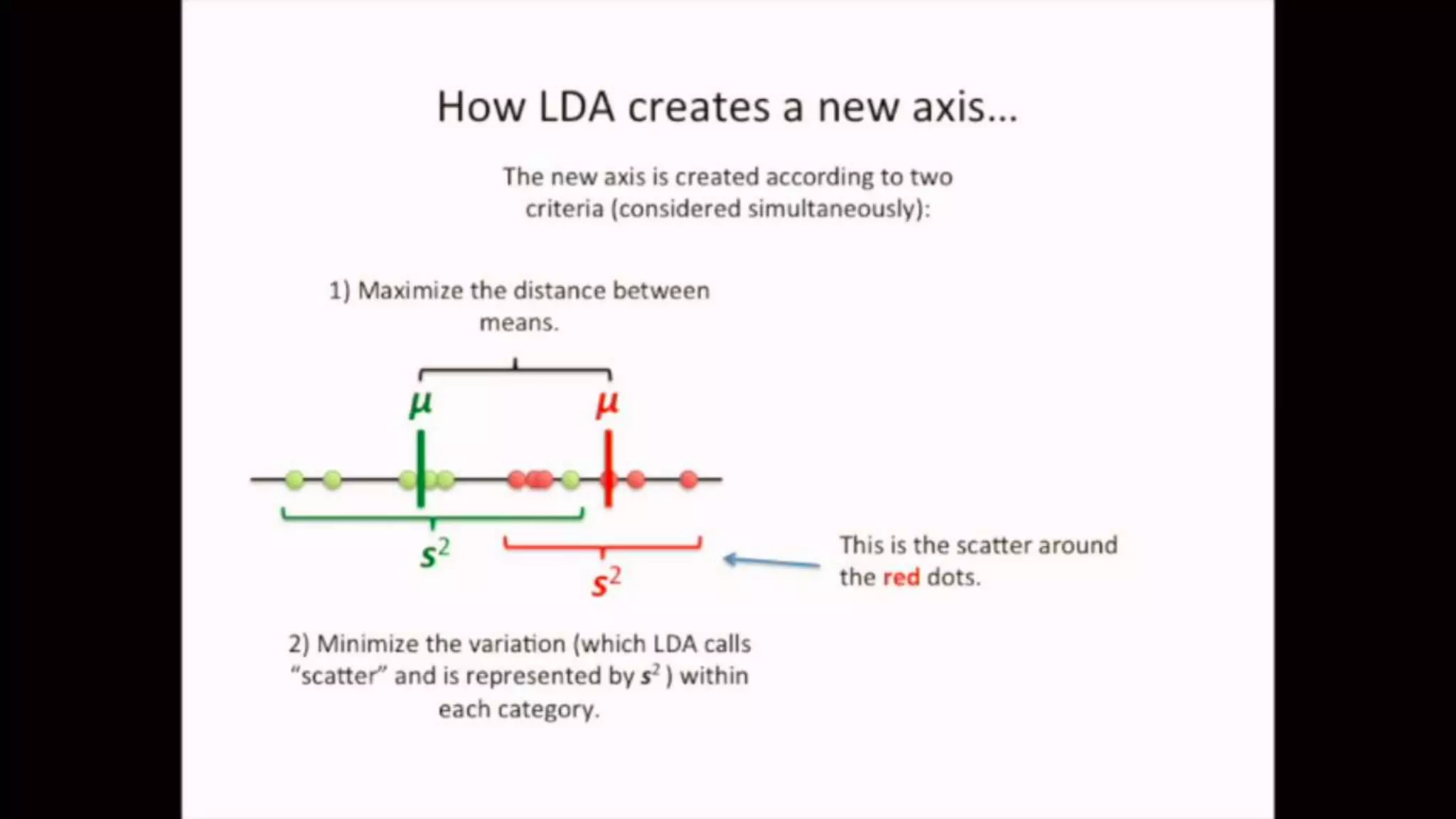
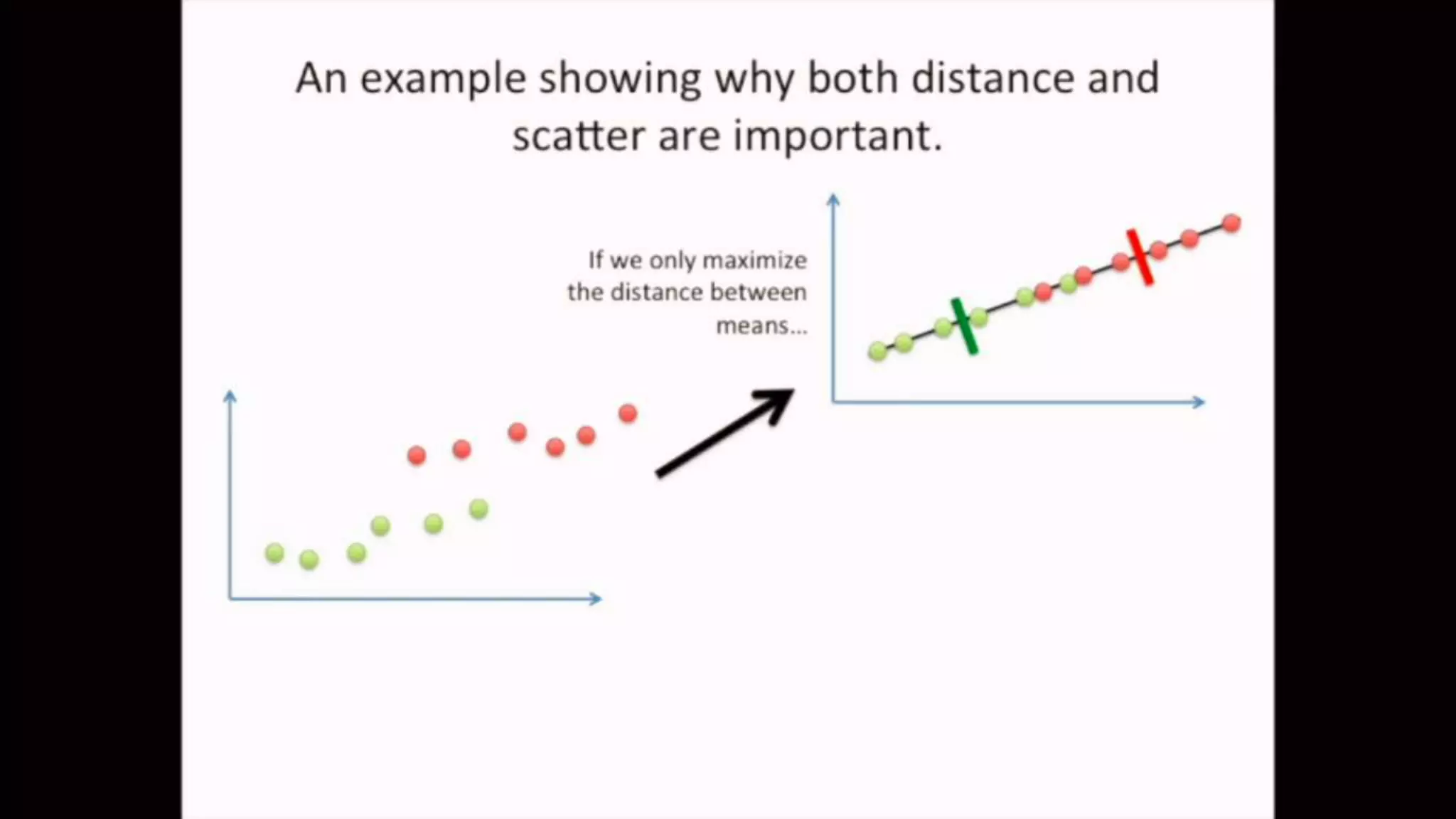
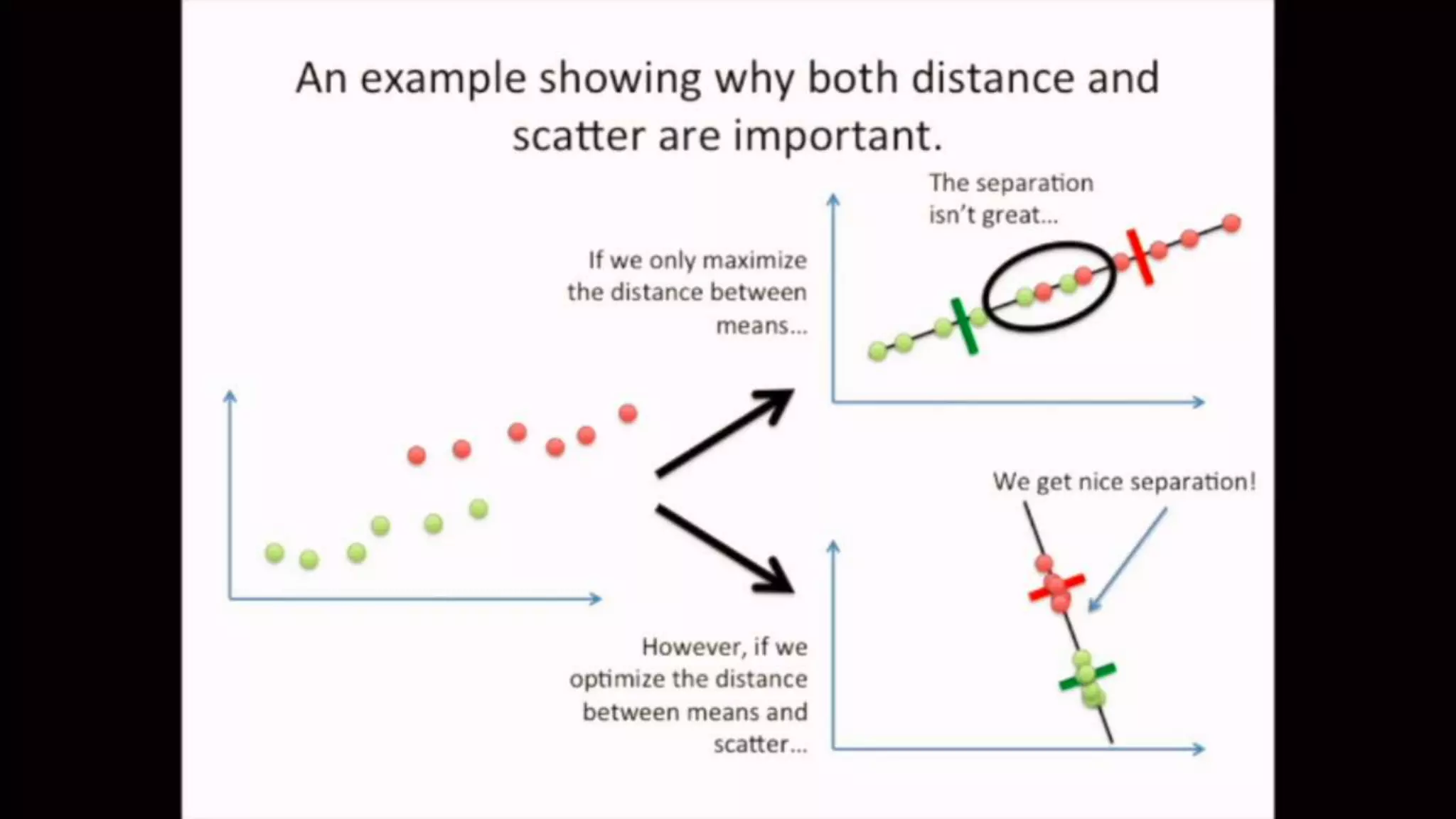
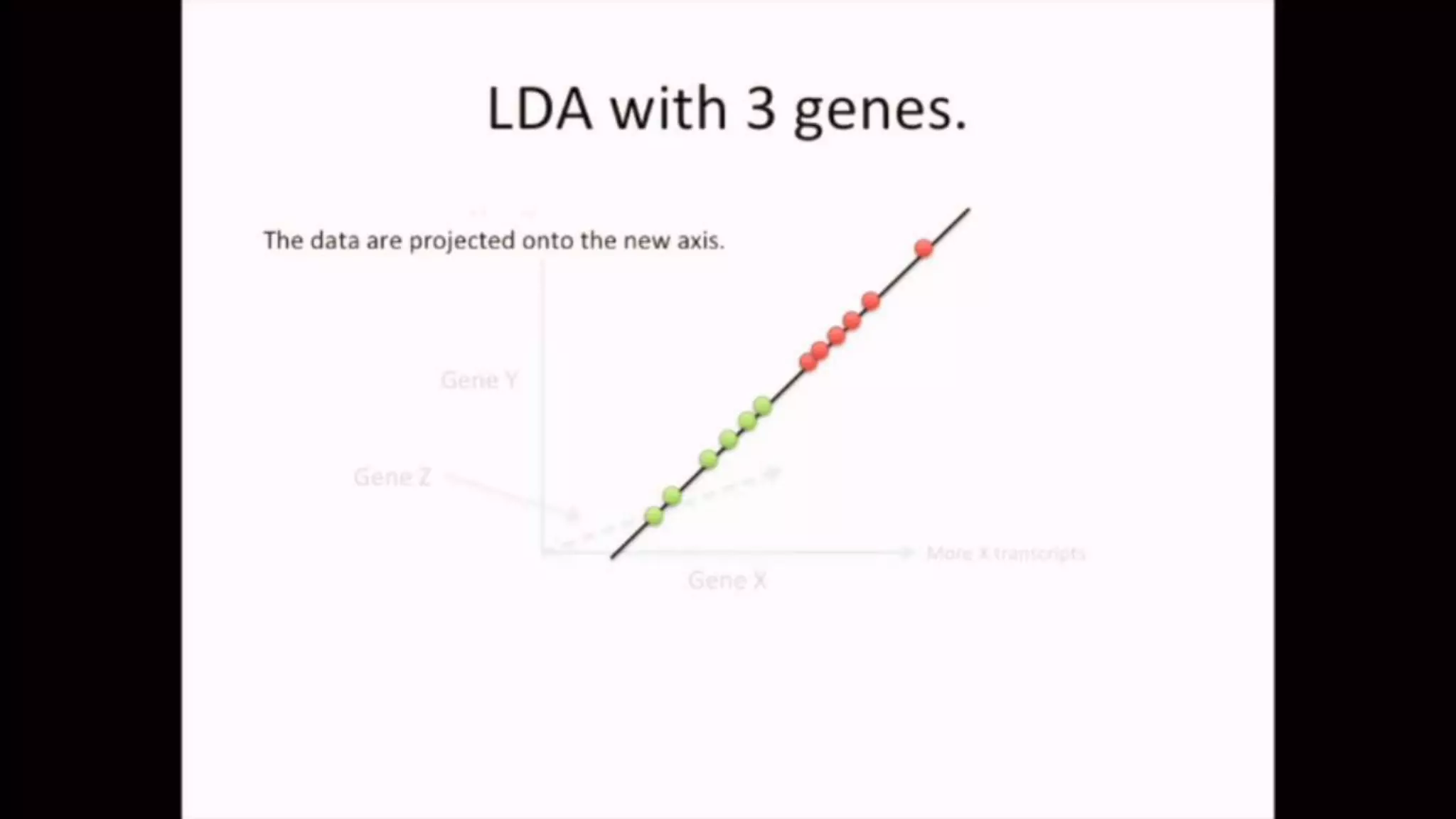
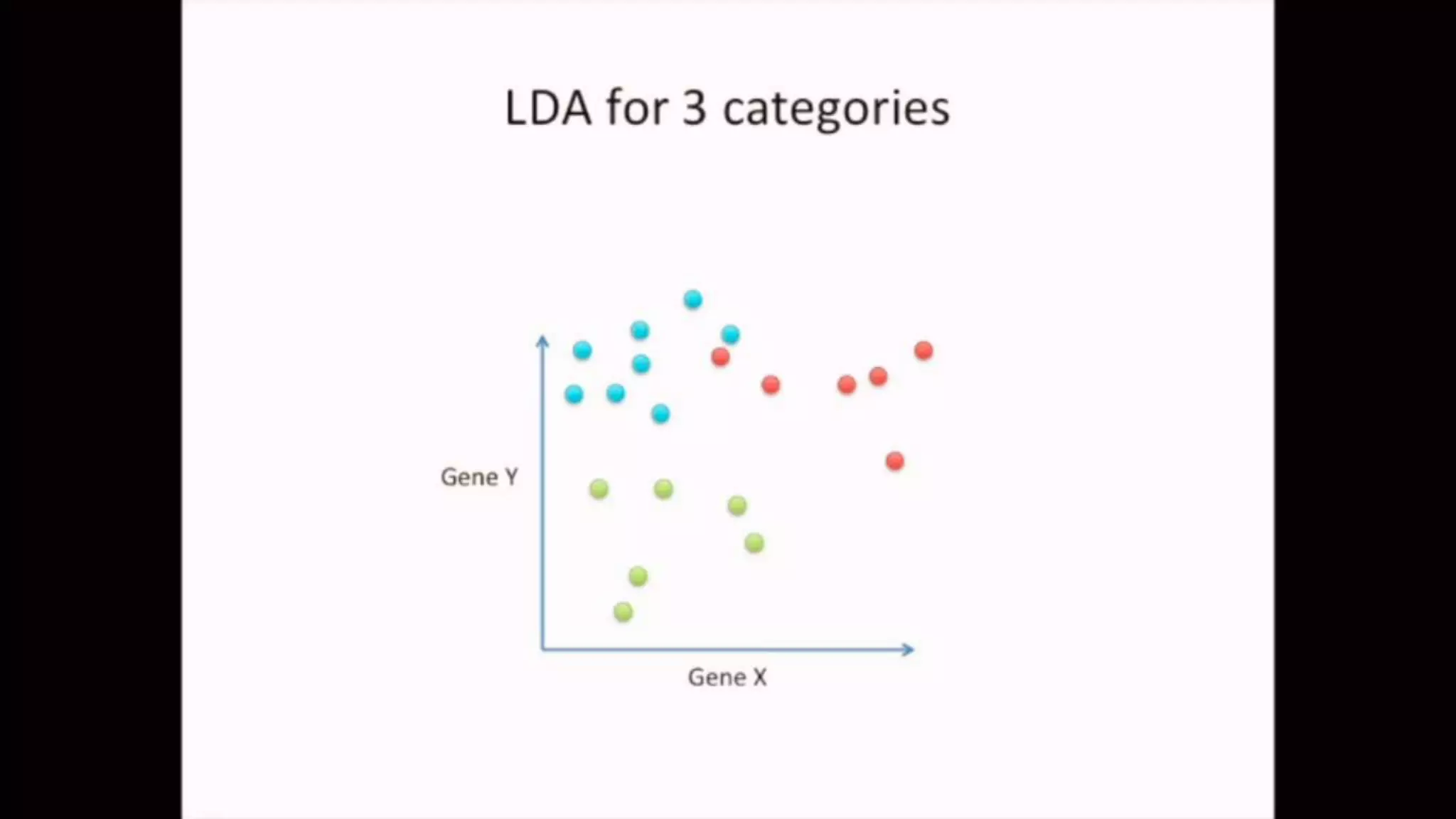
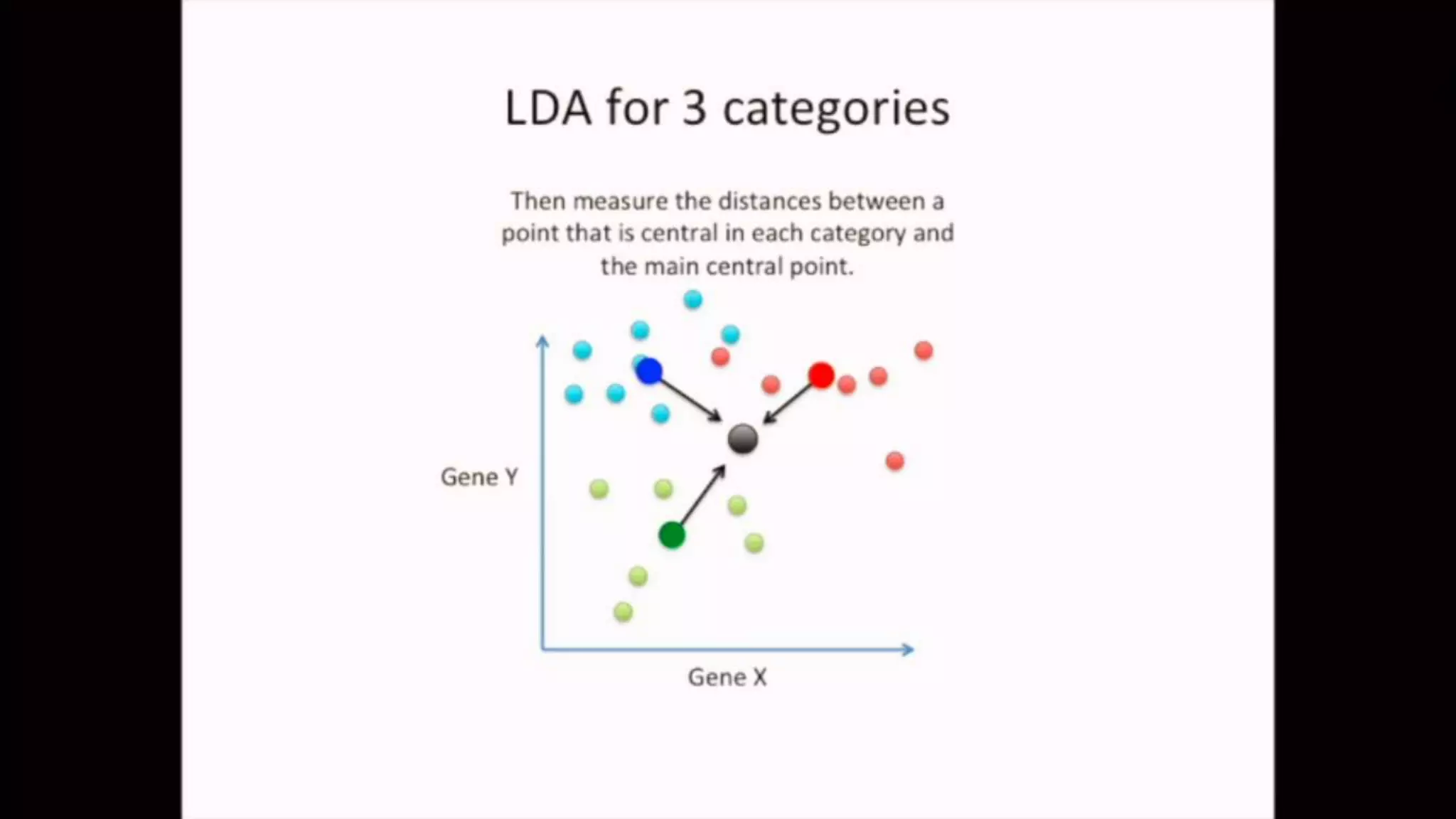
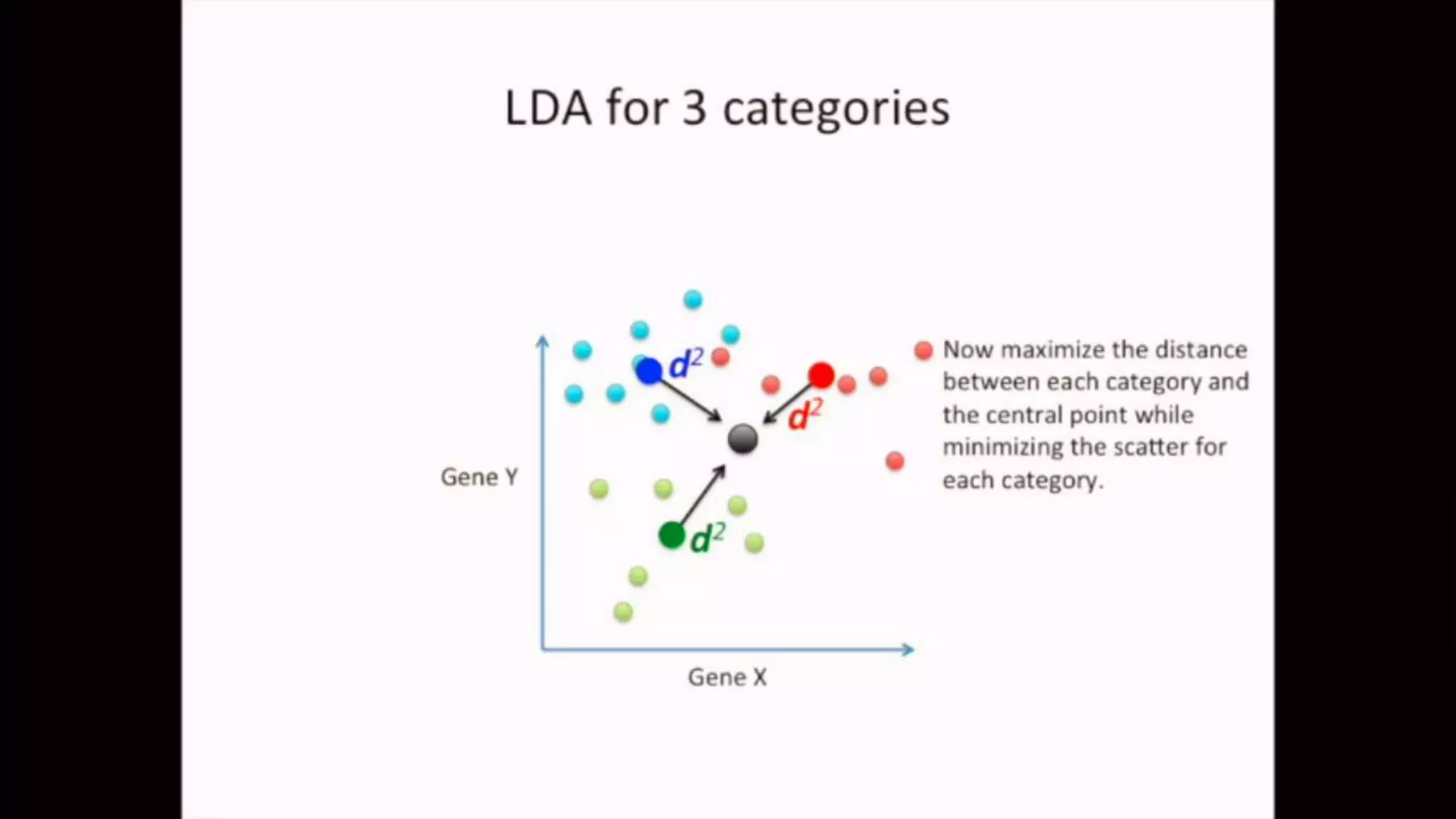
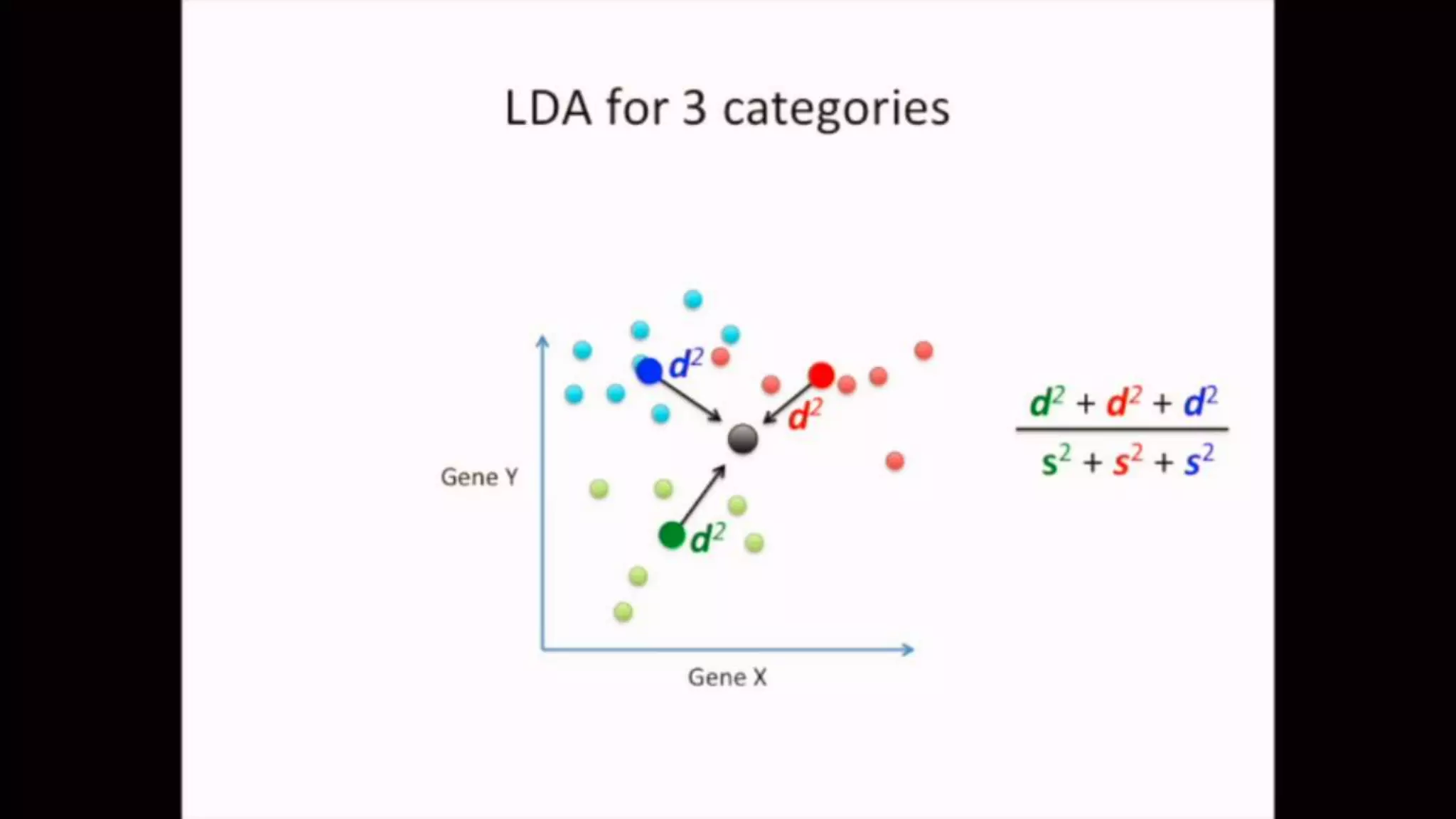
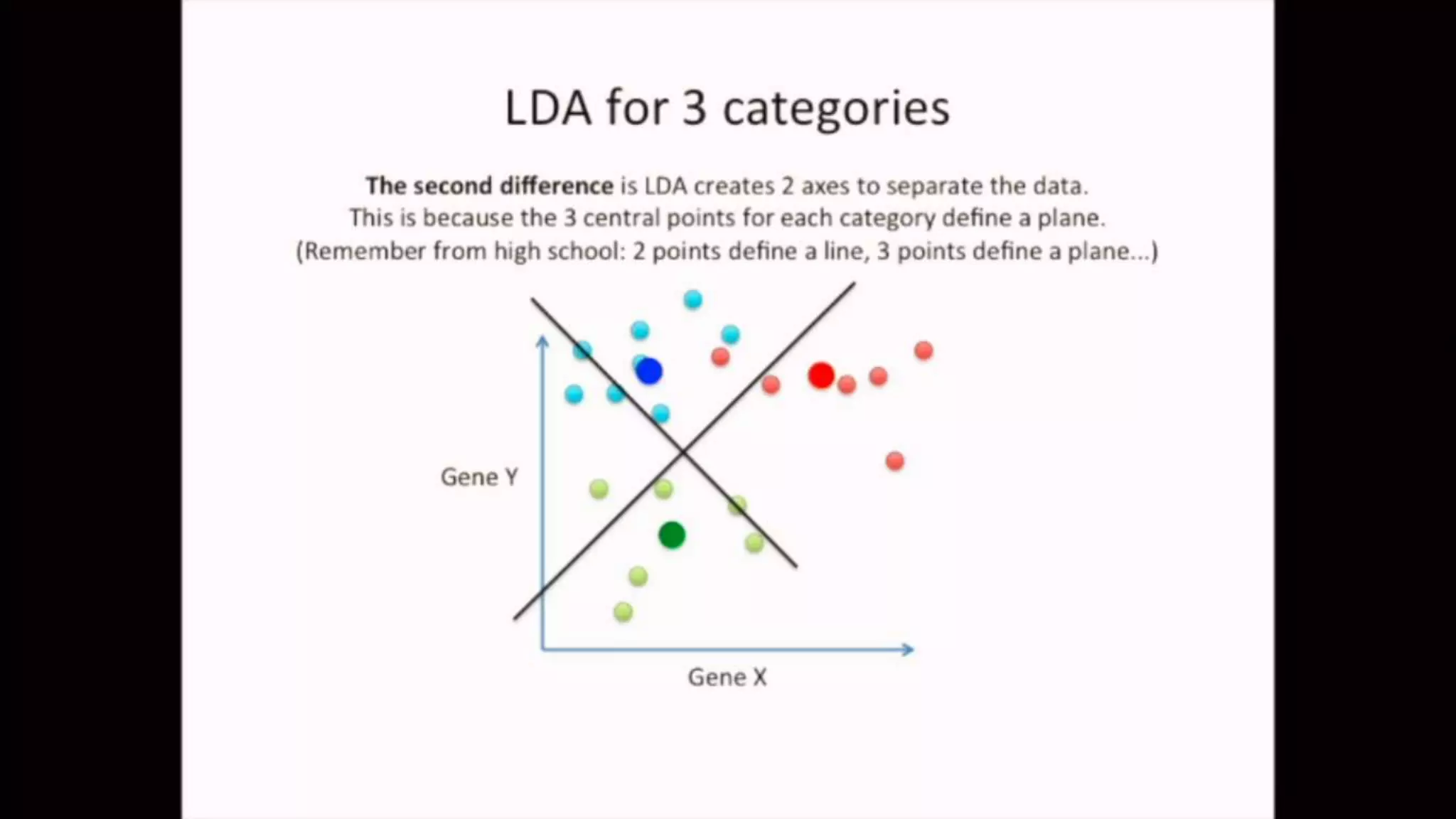
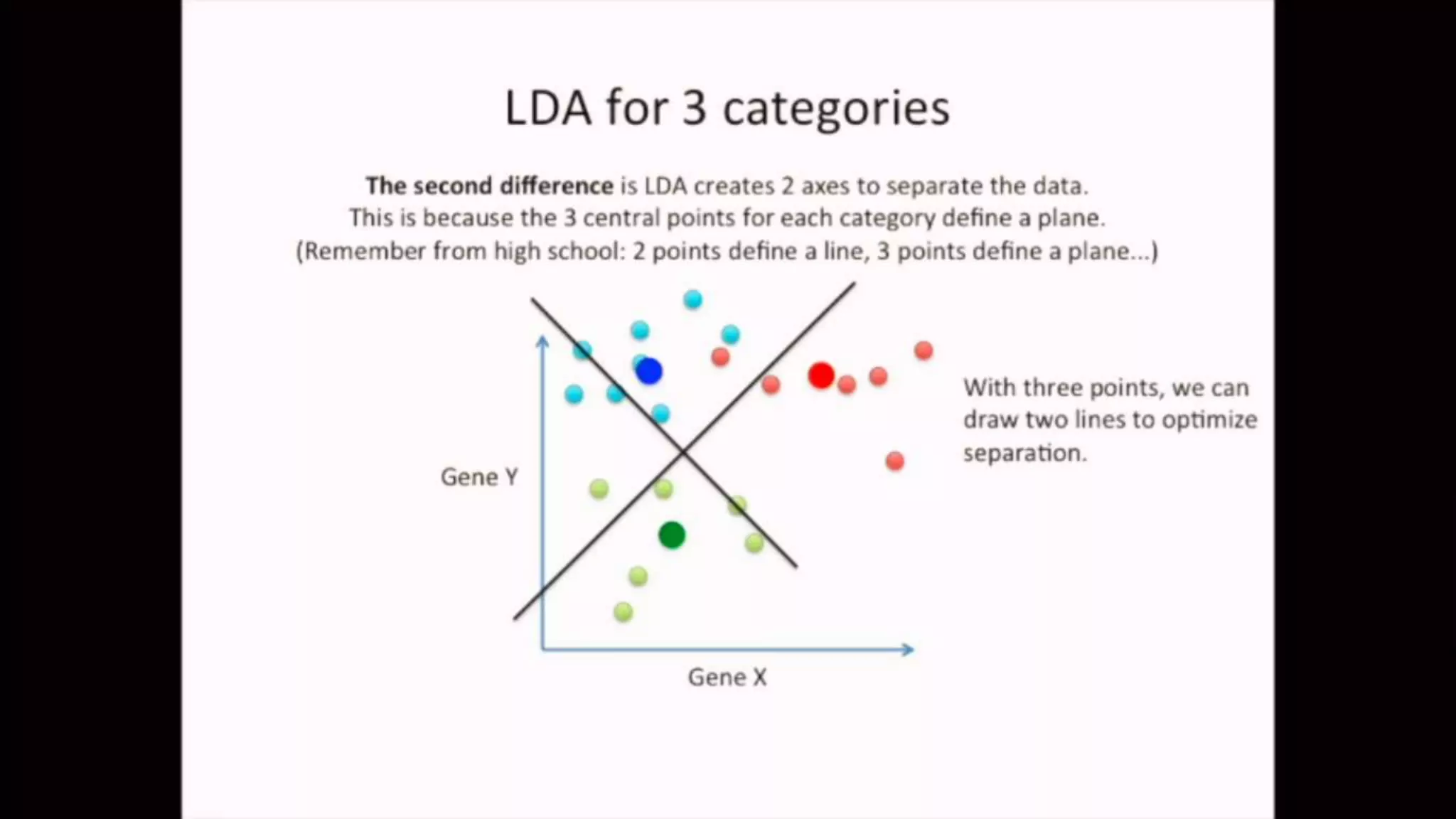
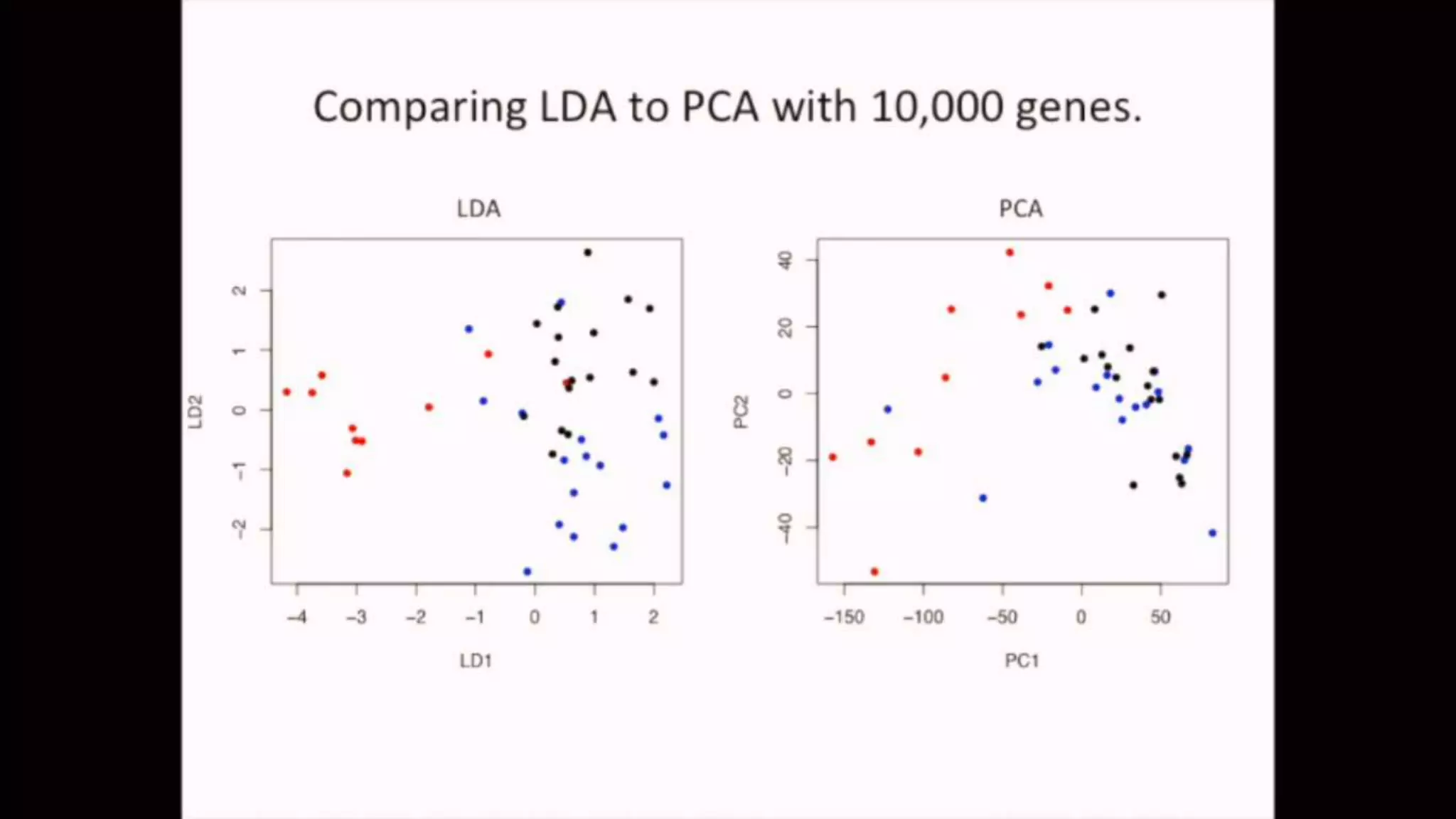
The document discusses Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA) as techniques for dimensionality reduction in machine learning. PCA is focused on maximizing variance retention while transforming correlated variables into principal components, whereas LDA aims to maximize class separability to improve classification performance. The text also includes Python code examples for implementing PCA and LDA, highlighting their applications in various domains such as finance and image processing.

1. PCA AND LDA (MACHINE
LEARNING)
Akhilesh Joshi
akhileshjoshi123@gmail
.com

2. PCA

3. PRINCIPAL COMPONENT ANALYSIS
DEFINED
The main idea of principal component analysis (PCA) is to reduce the
dimensionality of a data set consisting of many variables correlated
with each other, either heavily or lightly, while retaining the variation
present in the dataset, up to the maximum extent.
The same is done by transforming the variables to a new set of
variables, which are known as the principal components (or simply,
the PCs) and are orthogonal, ordered such that the retention of
variation present in the original variables decreases as we move down
in the order.
So, in this way, the 1st principal component retains maximum
variation that was present in the original components. The principal
components are the eigenvectors of a covariance matrix, and hence
they are orthogonal.

6. REFERENCES
StatQuest :
https://www.youtube.com/watch?v=_UVHneBUBW0&list=RD_UVHneB
UBW0
Dezyre :
https://www.dezyre.com/data-science-in-python-tutorial/principal-
component-analysis-tutorial

7. PCA
CONCEPT
ILLUSTRATI
ON

97. IMPLEMENTING PCA ON A 2-D
DATASET
Step 1: Normalize the data
Step 2: Calculate the covariance matrix
Step 3: Calculate the eigenvalues and eigenvectors
Step 4: Choosing components and forming a feature vector
Step 5: Forming Principal Components:

98. APPLICATIONS OF PRINCIPAL
COMPONENT ANALYSIS
PCA is predominantly used as a dimensionality reduction technique in
domains like facial recognition, computer vision and image
compression. It is also used for finding patterns in data of high
dimension in the field of finance, data mining, bioinformatics,
psychology, etc.

100. LDA DEFINED
Linear Discriminant Analysis (LDA) is most commonly used as
dimensionality reduction technique in the pre-processing step for
pattern-classification and machine learning applications.
The goal is to project a dataset onto a lower-dimensional space with
good class-separability in order avoid overfitting (“curse of
dimensionality”) and also reduce computational costs.

103. LDA
CONCEPT
ILLUSTRATI
ON

173. APPLICATIONS
OF
LDA

174. PCA VS LDA
PCA as a technique that finds the
directions of maximal variance
LDA attempts to find a feature
subspace that maximizes class
separability

176. PYTHON
This Photo by Unknown Author is licensed under CC BY-SA

177. IMPORTING THE LIBRARIES
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

178. IMPORTING THE DATASET
dataset = pd.read_csv('Wine.csv')
X = dataset.iloc[:, 0:13].values
y = dataset.iloc[:, 13].values

179. SPLITTING THE DATASET INTO THE
TRAINING SET AND TEST SET
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2,
random_state = 0)

180. FEATURE SCALING
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)

181. APPLYING PCA
from sklearn.decomposition import PCA
pca = PCA(n_components = None) #just for testing
pca = PCA(n_components = 2)
X_train = pca.fit_transform(X_train)
X_test = pca.transform(X_test)
explained_variance = pca.explained_variance_ratio_
Feature scaling is must
before any
dimensionality
reduction method

182. APPLYING KERNEL PCA
from sklearn.decomposition import KernelPCA
kpca = KernelPCA(n_components = 2, kernel = 'rbf')
X_train = kpca.fit_transform(X_train)
X_test = kpca.transform(X_test)
Feature scaling is must
before any
dimensionality
reduction method

183. APPLYING LDA
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
as LDA
lda = LDA(n_components = 2)
X_train = lda.fit_transform(X_train, y_train)
X_test = lda.transform(X_test)
Feature scaling is must
before any
dimensionality
reduction method

184. FITTING LOGISTIC REGRESSION
TO THE TRAINING SET
from sklearn.linear_model import LogisticRegression
classifier = LogisticRegression(random_state = 0)
classifier.fit(X_train, y_train)

185. PREDICTING THE TEST SET
RESULTS
y_pred = classifier.predict(X_test)

186. # MAKING THE CONFUSION MATRIX
from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)

187. from matplotlib.colors import ListedColormap
X_set, y_set = X_train, y_train
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step = 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green', 'blue')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green', 'blue'))(i), label = j)
plt.title('Logistic Regression (Training set)')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.legend()
plt.show()

188. # Visualising the Test set results
from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:, 0].min() - 1, stop = X_set[:, 0].max() + 1, step
= 0.01),
np.arange(start = X_set[:, 1].min() - 1, stop = X_set[:, 1].max() + 1, step = 0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('red', 'green', 'blue')))
plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())
for i, j in enumerate(np.unique(y_set)):
plt.scatter(X_set[y_set == j, 0], X_set[y_set == j, 1],
c = ListedColormap(('red', 'green', 'blue'))(i), label = j)
plt.title('Logistic Regression (Test set)')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.legend()
plt.show()