Download to read offline
Uploaded bycairo university
Machine Learning lecture3(linear regression)
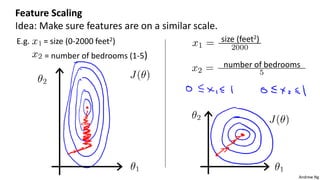
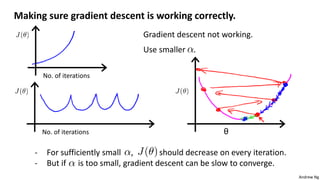
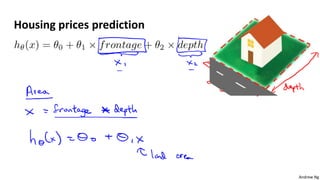
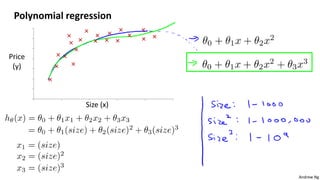
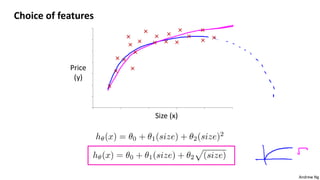
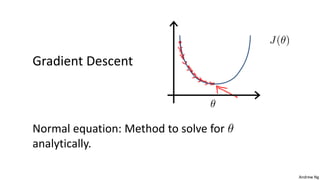
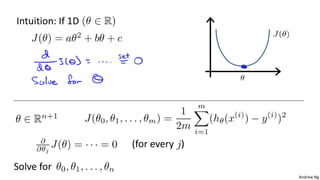
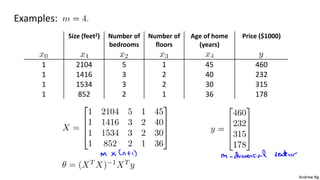
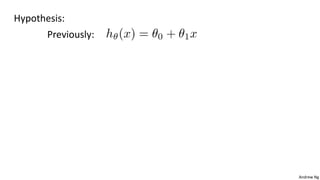This document discusses linear regression with multiple variables. It introduces notation for multiple features and describes using gradient descent to update the parameters simultaneously for each feature. Feature scaling is introduced to standardize the ranges of different features. Choosing an appropriate learning rate for gradient descent is also discussed. The document covers using polynomial regression by adding powers of features. It also describes solving for the parameters analytically using the normal equation and issues that can arise with non-invertibility.
More Related Content
Similar to Machine Learning lecture3(linear regression)
Machine Learning lecture3(linear regression)
- 1. Linear Regression with multiplevariables Multiple features Machine Learning
- 2. Andrew Ng Size (feet2)Price ($1000) 2104 460 1416 232 1534 315 852 178 … … Multiple features (variables)
- 3. Andrew Ng Size (feet2)Number of bedrooms Number of floors Age of home (years) Price ($1000) 2104 5 1 45 460 1416 3 2 40 232 1534 3 2 30 315 852 2 1 36 178 … … … … … Multiple features (variables). Notation: = number of features = input (features) of training example. = value of feature in training example.
- 4.
- 5. Andrew Ng For convenienceof notation, define . Multivariate linear regression.
- 6. Linear Regression with multiplevariables Gradient descent for multiple variables Machine Learning
- 7. Andrew Ng Hypothesis: Cost function: Parameters: (simultaneouslyupdate for every ) Repeat Gradient descent:
- 8. Andrew Ng (simultaneously update) Gradient Descent Repeat Previously (n=1): New algorithm : Repeat (simultaneously update for )
- 9. Linear Regression with multiplevariables Gradient descent in practice I: Feature Scaling Machine Learning
- 10. Andrew Ng E.g. =size (0-2000 feet2) = number of bedrooms (1-5) Feature Scaling Idea: Make sure features are on a similar scale. size (feet2) number of bedrooms
- 11. Andrew Ng Feature Scaling Getevery feature into approximately a range.
- 12. Andrew Ng Replace withto make features have approximately zero mean (Do not apply to ). Mean normalization E.g.
- 13. Linear Regression with multiplevariables Gradient descent in practice II: Learning rate Machine Learning
- 14. Andrew Ng Gradient descent -“Debugging”: How to make sure gradient descent is working correctly. - How to choose learning rate .
- 15. Andrew Ng Example automatic convergencetest: Declare convergence if decreases by less than in one iteration. 0 100 200 300 400 No. of iterations Making sure gradient descent is working correctly. Or,
- 16. Andrew Ng Making suregradient descent is working correctly. Gradient descent not working. Use smaller . No. of iterations No. of iterations θ - For sufficiently small , should decrease on every iteration. - But if is too small, gradient descent can be slow to converge.
- 17. Andrew Ng Summary: - Ifis too small: slow convergence. - If is too large: may not decrease on every iteration; may not converge. To choose , try . . ., 0.001, , 0.01, , 0.1, , 1, . . .
- 18. Linear Regression with multiplevariables Features and polynomial regression Machine Learning
- 19. Andrew Ng Housing pricesprediction
- 20.
- 21. Andrew Ng Choice offeatures Price (y) Size (x)
- 22. Linear Regression with multiplevariables Normal equation Machine Learning
- 23. Andrew Ng Gradient Descent Normalequation: Method to solve for analytically.
- 24. Andrew Ng Intuition: If1D Solve for (for every )
- 25. Andrew Ng Size (feet2)Number of bedrooms Number of floors Age of home (years) Price ($1000) 1 2104 5 1 45 460 1 1416 3 2 40 232 1 1534 3 2 30 315 1 852 2 1 36 178 Size (feet2) Number of bedrooms Number of floors Age of home (years) Price ($1000) 2104 5 1 45 460 1416 3 2 40 232 1534 3 2 30 315 852 2 1 36 178 Examples:
- 26. Andrew Ng examples ;features. E.g. If
- 27. Andrew Ng is inverseof matrix . Octave: pinv(X’*X)*X’*y
- 28. Andrew Ng training examples,features. Gradient Descent Normal Equation • No need to choose . • Don’t need to iterate. • Need to choose . • Needs many iterations. • Works well even when is large. • Need to compute • Slow if is very large.
- 29. Linear Regression with multiplevariables Normal equation and non-invertibility (optional) Machine Learning
- 30. Andrew Ng Normal equation -What if is non-invertible? (singular/ degenerate) - Octave: pinv(X’*X)*X’*y
- 31. Andrew Ng What ifis non-invertible? • Redundant features (linearly dependent). E.g. size in feet2 size in m2 • Too many features (e.g. ). - Delete some features, or use regularization.
Editor's Notes
- #5 Pop-up Quiz
- #12 Features should take a similar range of values. This leads to a faster convergence of the gradient descent.
- #13 The feature range of values shouldn’t be very large and also not very tiny. Or, it shouldn’t be far from the -1 to +1 range.
- #17 Debugging by plotting cost function J versus no. of iterations of the algorithm. The algorithm works well as J decreases in the plot. The plot also shows where the algorithm converges as the curve becomes flattened. Choosing the threshold in the automatic convergence test is difficult.
- #19 We try to pick the largest possible reasonable value for the learning rate to ensure a fast convergence.
- #21 We can define new features to get a better model.
- #22 We can fit the polynomial function to the linear regression model by redefining or choosing features. In this case, feature scaling becomes extremely important.
- #23 This slide shows another different choice for your features.
- #27 Pop-up Quiz
- #28 Pop-up Quiz
- #30 Feature scaling is not necessary here.
- #31 As the no. of features is less than 1000, the normal equation method is useful. When the model becomes more complicated n> 1000, better use gradient descent.
- #34 Regularization enables to fit a large no. of parameters using a small no. of training examples.