A first order low pass filter was modeled using an RC circuit with a 460 ohm resistor and 0.05 microfarad capacitor. The experimental cutoff frequency was found to be 9,000 ± 400 Hz, which matched the simulated value. The experimental amplitude response and phase response also matched theoretical values, except at 1 MHz where discrepancies occurred likely due to limitations of the waveform generator and modeling assumptions at high frequencies. Overall, the first order RC circuit model accurately predicted the filter characteristics except at very high frequencies.

1. 2016-07-20
First Order Low Pass Filter Equation Modeling with
RC Circuit
Ross Rozanski
AME 341a: Mechoptronics I
University of Southern California
Abstract
A first order low pass filter was modelled using an RC circuit. A
resistor of 460.0 ± 0.5 Ω and a capacitor with a rating of 0.05 μF
were used. Experimental values for the amplitude and phase
response were acquired from the circuit, the circuit was recreated
in a simulation program, and the characteristics were compared.
The characteristics of interest were the cutoff frequency, amplitude
response, and the phase response. Frequency range tested was from
10 Hz to 1 MHz. The experimental value of the cutoff frequency
was 9,000 ± 400 Hz, which was equal to the acquired simulation
values. Furthermore, the measured amplitude response and phase
response were equal to each other and the expected theoretical
values. However, experimental values and theoretical values did
not match at the frequency of 1 MHz and caution should be taken
with comparable RC circuits when the voltage signal is of such
high frequency.
1 Introduction
Low pass filters (LPFs) are systems that only allow signals below a particular frequency to be
transmitted. Signals higher than this particular frequency, which is called the cutoff frequency

2. (fo), are diminished or attenuated. For voltage signals, an LPF can be constructed with an resistor
capacitor (RC) circuit. LPFs are used in audio equipment like subwoofers and speakers, radio
transmitters, and telephone lines with DSL splitters.
LPFs are partly defined by their order, which determines the amount frequencies above fo are
attenuated. For a first order LPF, the signal amplitude is reduced by half each time the frequency
is doubled. The relationship between the input and output of the first order LPF is given in
Equation 1, in which ei is the input voltage and eo is the output voltage.
RC(deo/dt) + eo = ei
A transfer function, which is a ratio of the input and output that describes the system, can be
derived from Equation 1 and yields Equation 2. 𝜔=2πf, and μ is a characteristic of the system,
defined as μ = RC. fo is characterized by H = 0.707 when 𝜔μ = 1, in which signals with
frequency any greater than fo are attenuated. The corresponding B and A are the output and input
of the system, respectively. Equation 2 is known as the amplitude response and is a quantitative
measure of the system at a given frequency.
𝐻 = |
𝐵
𝐴
| = √
1
1+𝑤2 𝜇2
By plotting the amplitude response onto a phasor diagram, another qualitative measure of the
system is obtained and is called the phase response. The amplitude response of Equation 2 and
the phase response of Equation 3 allow the behavior of the LPF first order equation to be
predicted.
𝜙 = tan-1
(-wμ)
When fo is characterized by H = 0.707, wμ =1, and 𝜙 = -45°. Due to this relationship, Equation 4
is obtained and defines fo.
fo =
1
2𝜋𝑅𝐶
Therefore, a theoretical value for fo is obtained for an LPF constructed of an RC circuit. A
simulated Bode plot is another method that can give a value for fo . A Bode plot is a log-log plot
of 20log10(H). These values can be compared to experimental and simulated values of fo.
2 Procedure
A low pass RC filter was set up on a circuit breadboard, shown in Figure 1. The digital
oscilloscope (DScope) used was a Tektronix TDS2014C Oscilloscope. The waveform generator
connected to the signal and ground of the circuit was an Agilent 33220A 20 MHz Waveform
Generator.
(1)
(3)
(2)
(4)

3. Figure 1 – An RC low pass filter circuit. The bold lines represent the circuit itself. The lighter
lines are the probes connected to the DScope.
A resistor of 460.0 ± 0.5 Ω and a capacitor of with a rating of 0.05 μF were used.
Experimentally, input and output voltages were measured at frequencies from 10 Hz to 1 MHz
using the DScope. The sine waves were generated by the waveform generator. The amplitude
response H at each frequency was calculated using Equation 2.
An experimental value of fo was obtained when H approached 0.707. To calculate the phase
response, the sine waves of ei and eo were observed on the DScope, in which the time each wave
crossed the x-axis was measured. The difference between the two time quantities was
represented by Δ𝑡, with units of microseconds. Similar to calculating the amplitude response,
frequencies from 10 Hz to 1 MHz were generated and observed with the DScope. The phase
angle was calculated using Equation 5, in which 𝜔=2πf.
𝜙 = −𝜔Δt
After the amplitude response and the phase response were measured, the low pass RC filter was
replicated and simulated in the program MultiSim. A function generator and an oscilloscope
were used in the program in order to create the signals and measure B, A, and Δ𝑡. Once these
values were recorded, a Bode plotter was attached to the virtual circuit to obtain fo, in which the
cursor was at the -3 dB point. The same frequency range was used in the Bode plotter as used
with the physical wave generator and circuit.
(5)

4. 3 Results
The experimental values for fo, amplitude response, and phase response (at fo) are listed in Table
1.
Table 1 – Comparison of the experimental values to the simulated values.
Experimental Simulated,
Oscilloscope
Simulated, Bode Plot
Cutoff Frequency (fo)
[Hz]
9,000 ± 400 9,000 8,800 ± 800
Amplitude Response 0.70 ± 0.02 0.708 ± 0.001 0.71 ± 0.02
Phase Response
[Degrees]
-45 ± 3 -47 ± 2 -45.0 ± 0.1
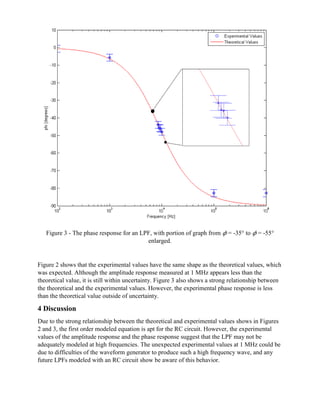
However, the frequency, amplitude response, and phase response acquired experimentally agree
with the simulated values. The Figures 2 and 3 show the experimental values of the amplitude
response H and the phase response 𝜙 plotted against frequency, in a log-log and a log-lin plot,
respectively. The areas of interest, H = 0.707 in Figure 2 and 𝜙 =-45° in Figure 3, were enlarged.
Figure 1
Figure 2 –The amplitude response for an LPF, with portion of graph from H = 10-0.1
to
H = 10-0.3
enlarged.

5. Figure 3 - The phase response for an LPF, with portion of graph from 𝜙 = -35° to 𝜙 = -55°
enlarged.
Figure 2 shows that the experimental values have the same shape as the theoretical values, which
was expected. Although the amplitude response measured at 1 MHz appears less than the
theoretical value, it is still within uncertainty. Figure 3 also shows a strong relationship between
the theoretical and the experimental values. However, the experimental phase response is less
than the theoretical value outside of uncertainty.
4 Discussion
Due to the strong relationship between the theoretical and experimental values shows in Figures
2 and 3, the first order modeled equation is apt for the RC circuit. However, the experimental
values of the amplitude response and the phase response suggest that the LPF may not be
adequately modeled at high frequencies. The unexpected experimental values at 1 MHz could be
due to difficulties of the waveform generator to produce such a high frequency wave, and any
future LPFs modeled with an RC circuit show be aware of this behavior.

6. References
Matlab Amplitude Response Code
clc;
clear all;
close all;
filename = 'A3 Graphs.xlsx';
A = xlsread(filename);
x=A(:,1);
y=A(:,2);
e=A(:,3);
g=[10:10:1000000];
R=460;
C=3.844*(10^(-8));
f=2*pi*g;
w=(R*C*f).^2;
j=(1./(1+w).^(1/2));
loglog(x,y,'ob');
hold on;
loglog(g,j,'-r');
errorbar(x,y,e,'.');
legend('Experimental Values','Theoretical Values' ); %inserts legend
and labels axes
xlabel('Frequency [Hz]');
ylabel('H');
axis([100 10^6 0 1]);
fullpath_filename = 'C:UsersRossPicturesGraph';
saveas(gcf,fullpath_filename,'png')

7. Matlab Phase Response Code
clc;
clear all;
close all;
filename = 'Book2.xlsx';
A = xlsread(filename);
x=A(:,1);
y=A(:,2);
e=A(:,3);
g=[10:10:1000000];
t=[0:20/99999:20]*10^((-6));
p=(-360)*t.*g;
f=atan(2*pi*g*460*(3.88*10^(-8)));
h=f*(-180/pi);
semilogx(x,y,'ob')
hold on;
semilogx(g,h,'-r');
errorbar(x,y,e,'.');
legend('Experimental Values','Theoretical Values' );
xlabel('Frequency [Hz]');
ylabel('phi [degrees]');
axis([100 10^6 0 -90]);
fullpath_filename = 'C:UsersRossPicturesGraphd';
saveas(gcf,fullpath_filename,'png')