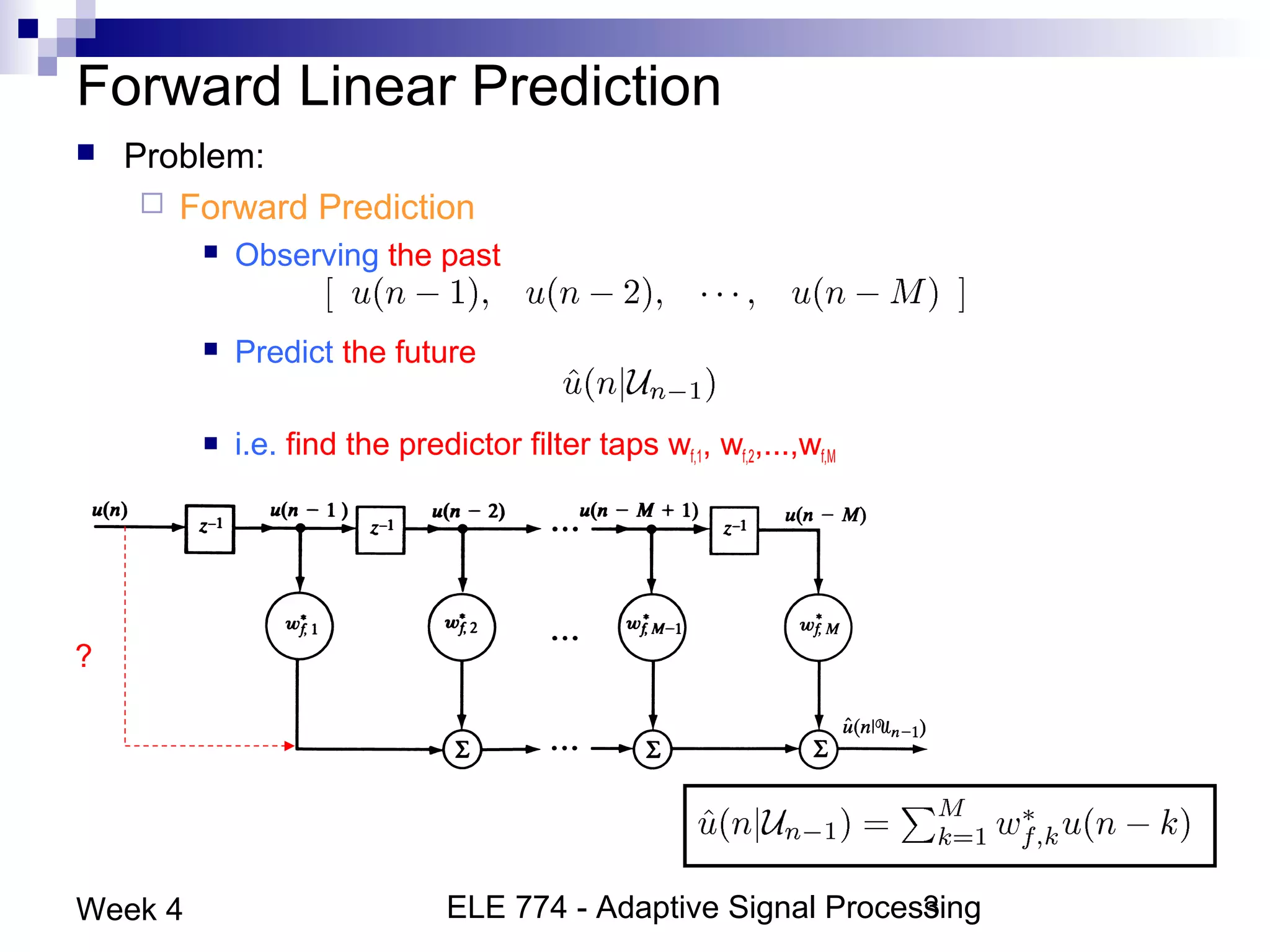
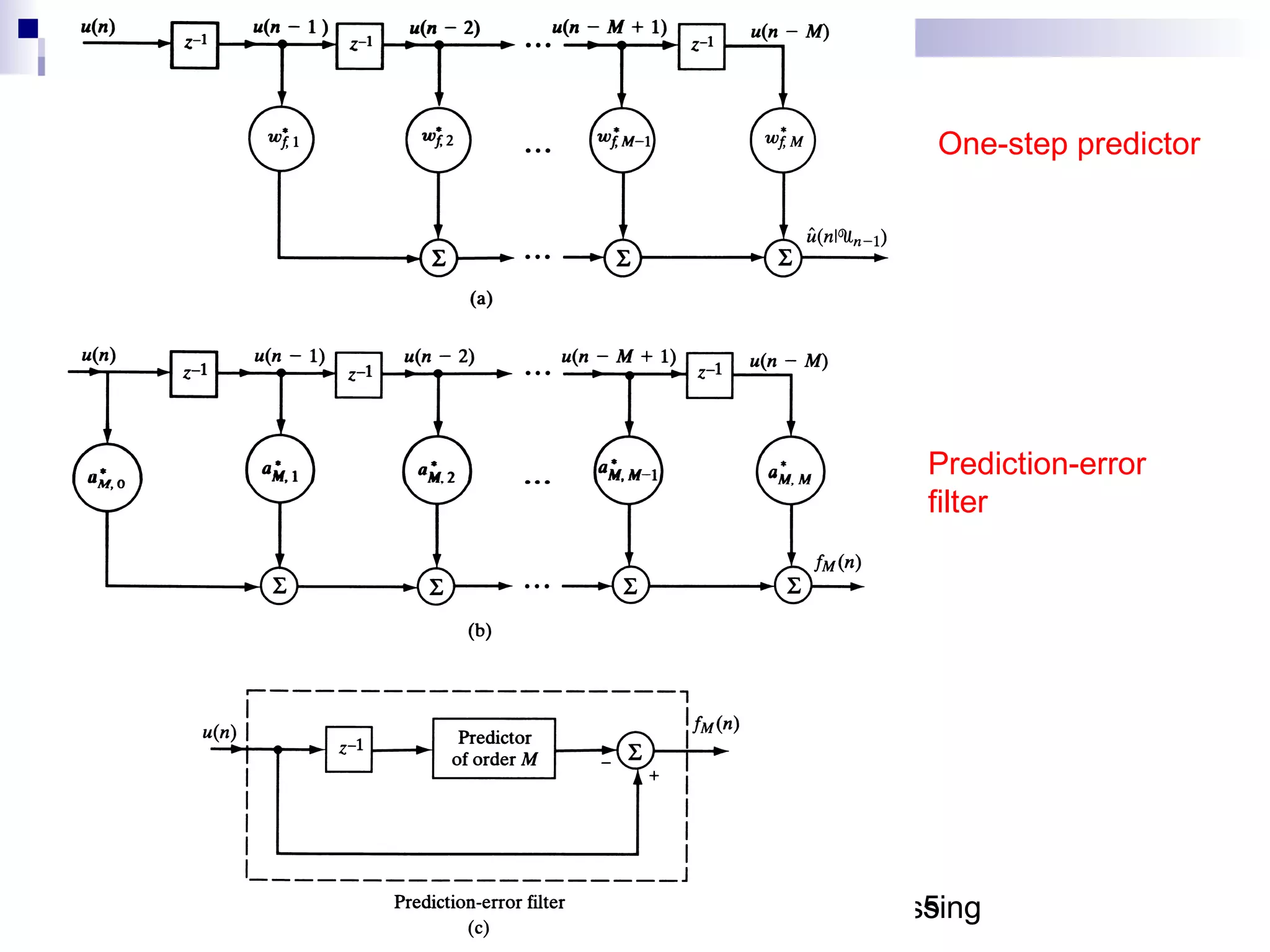
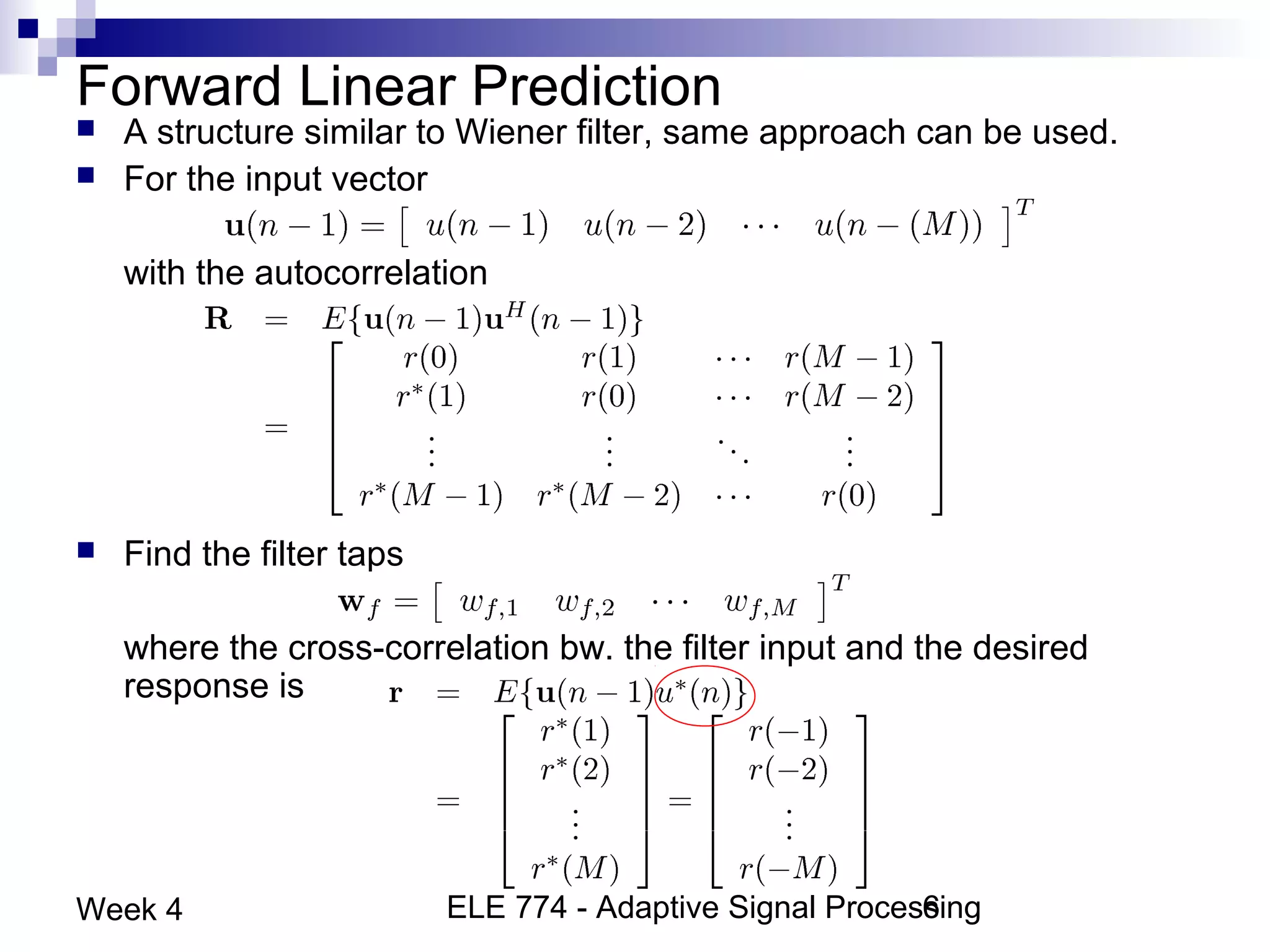
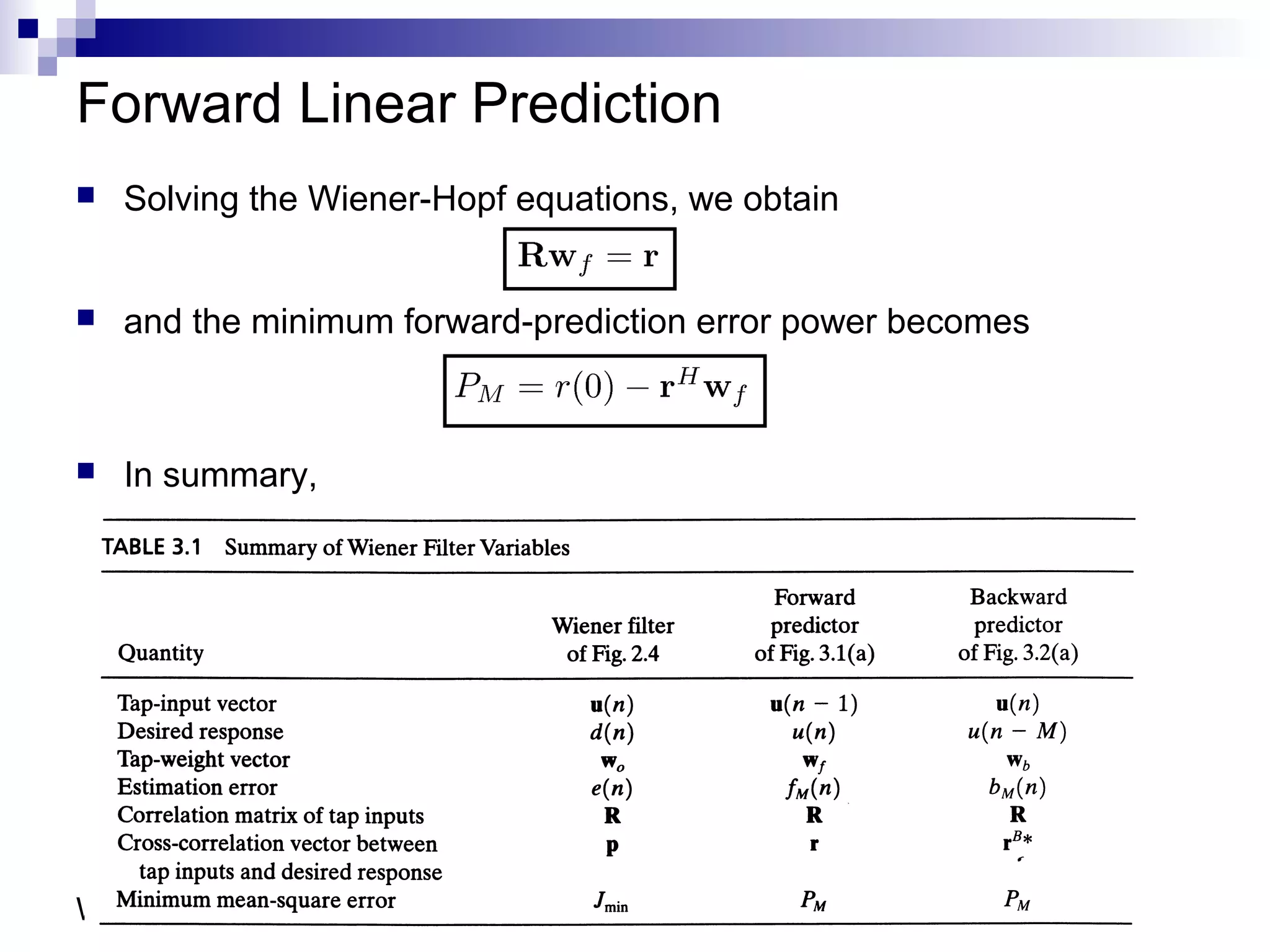
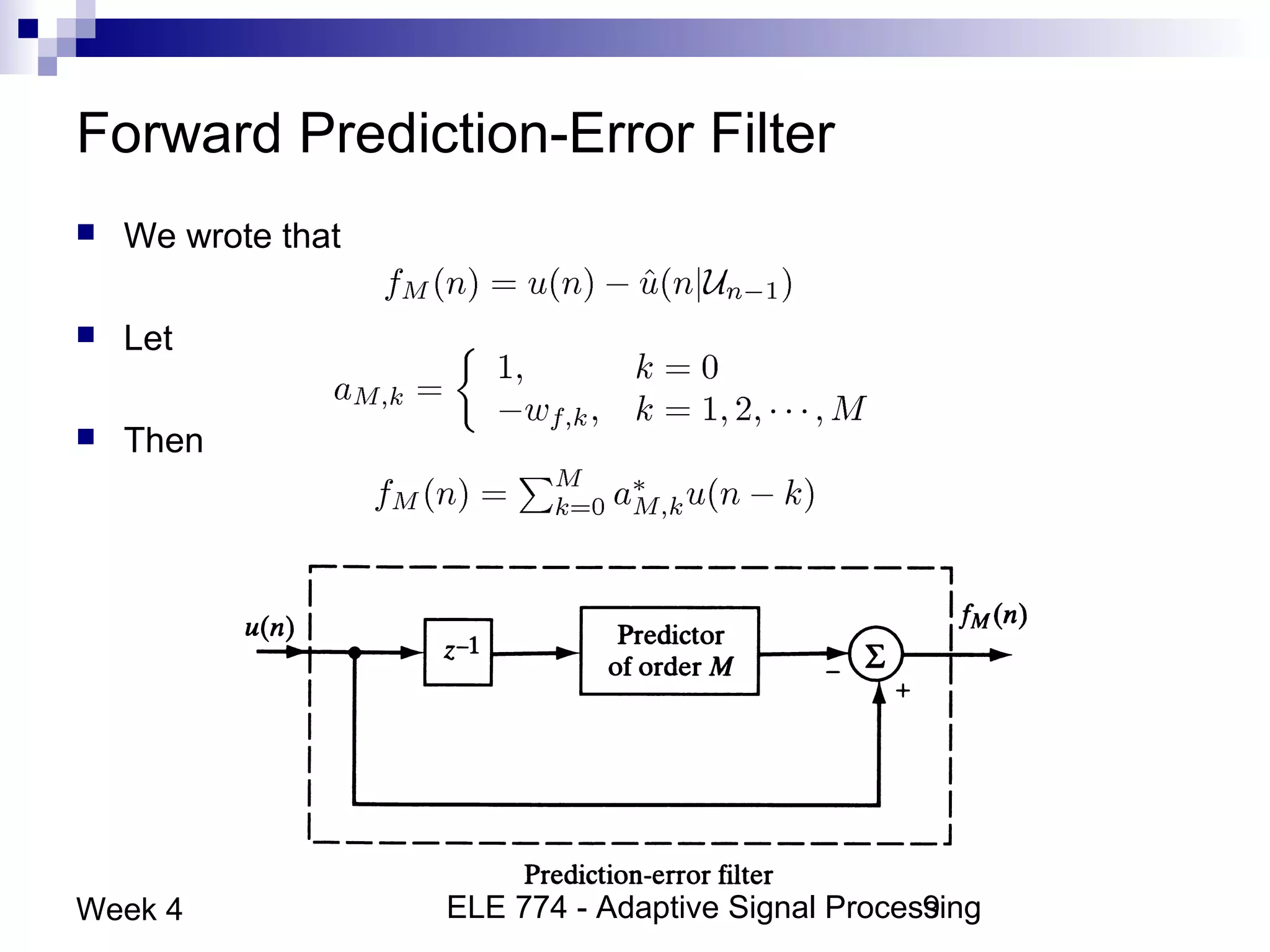
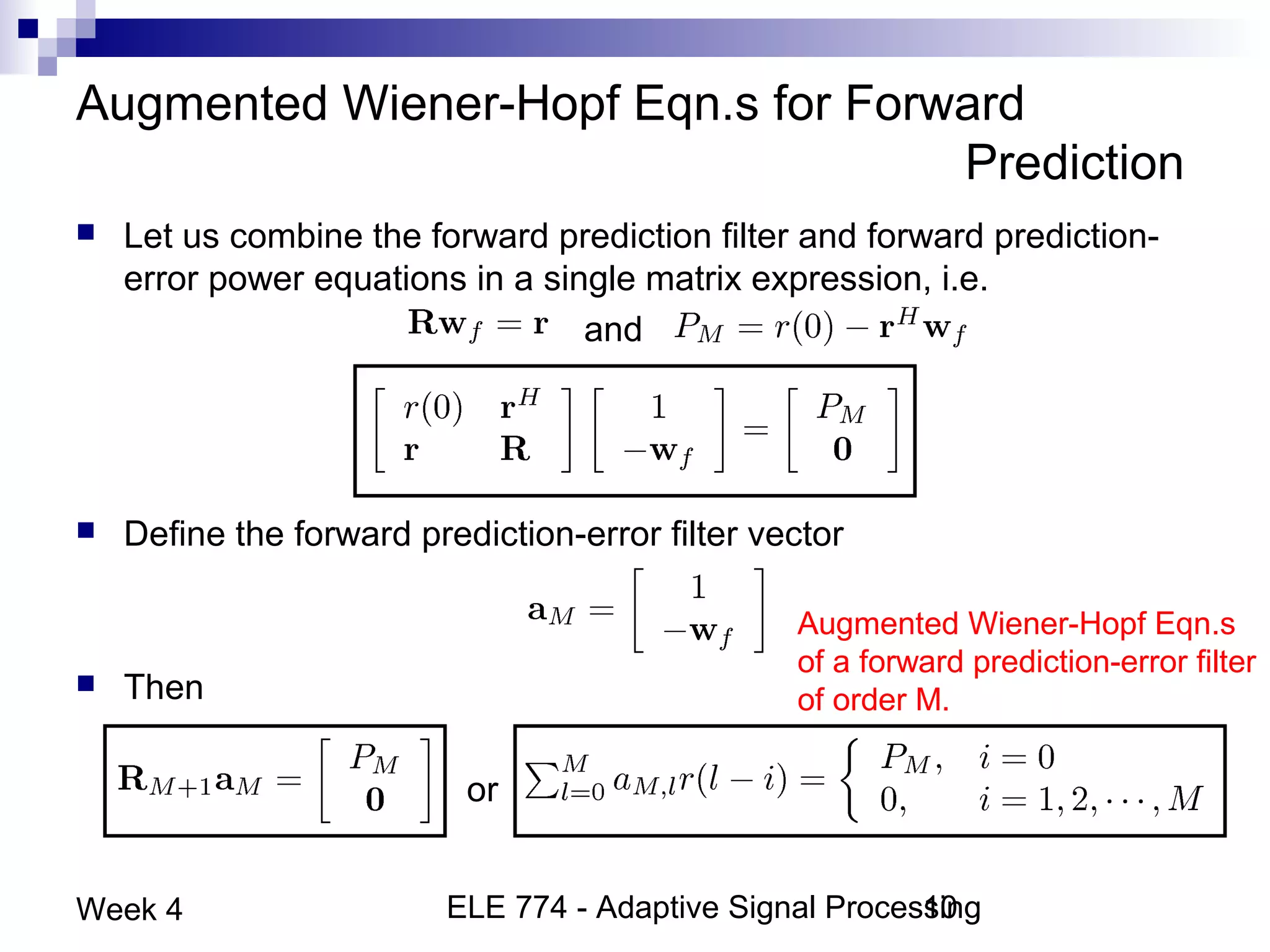
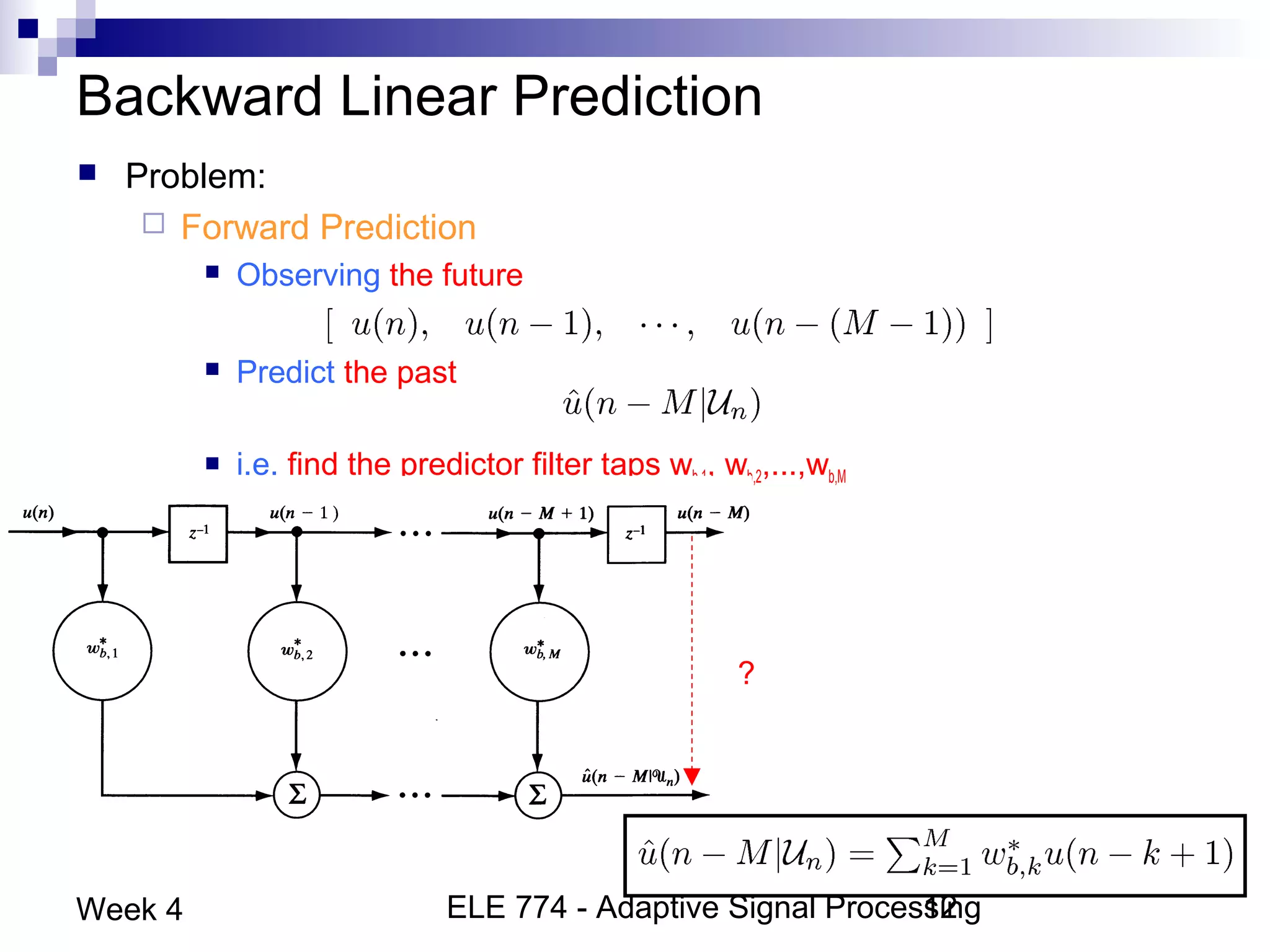
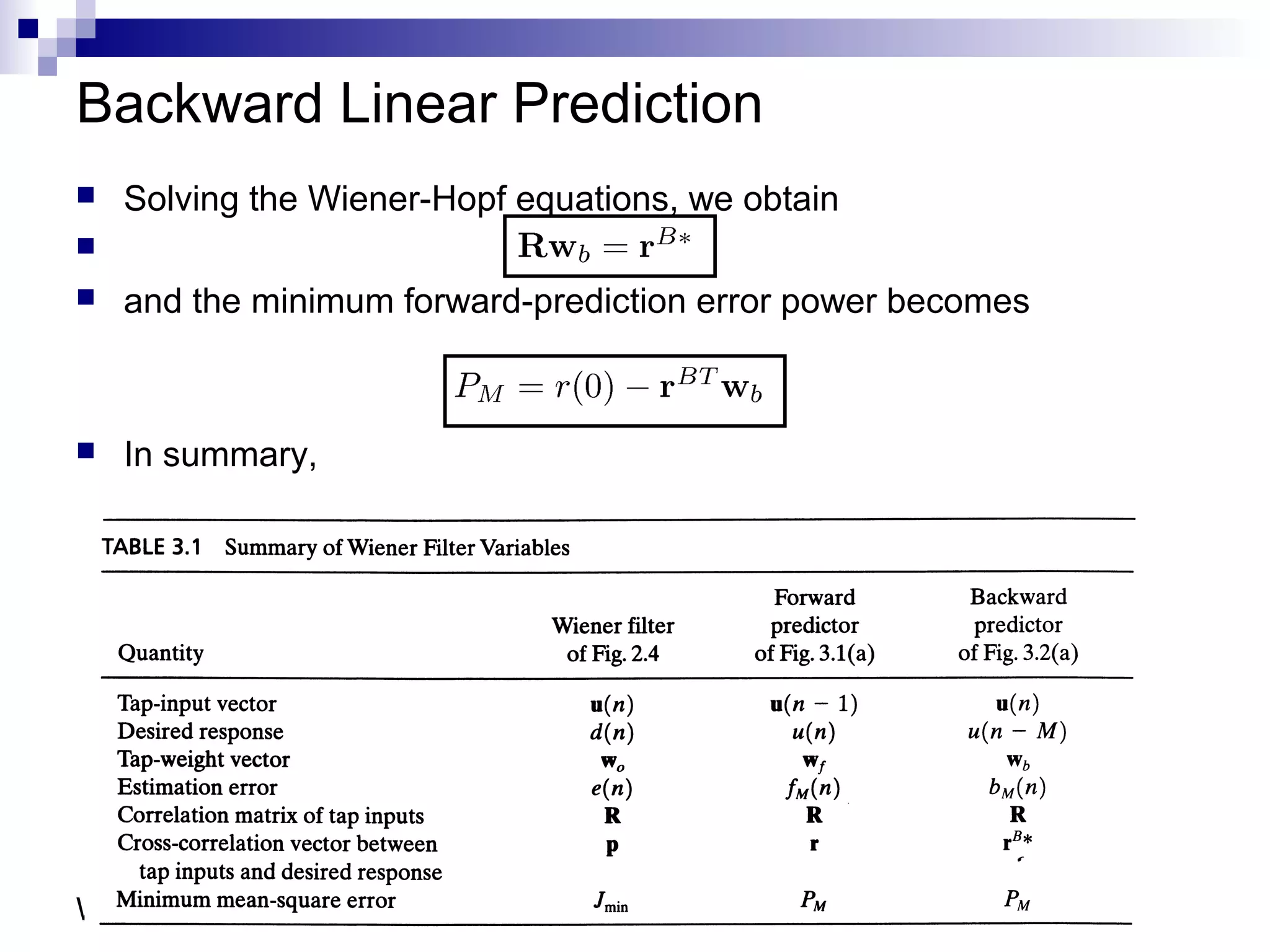
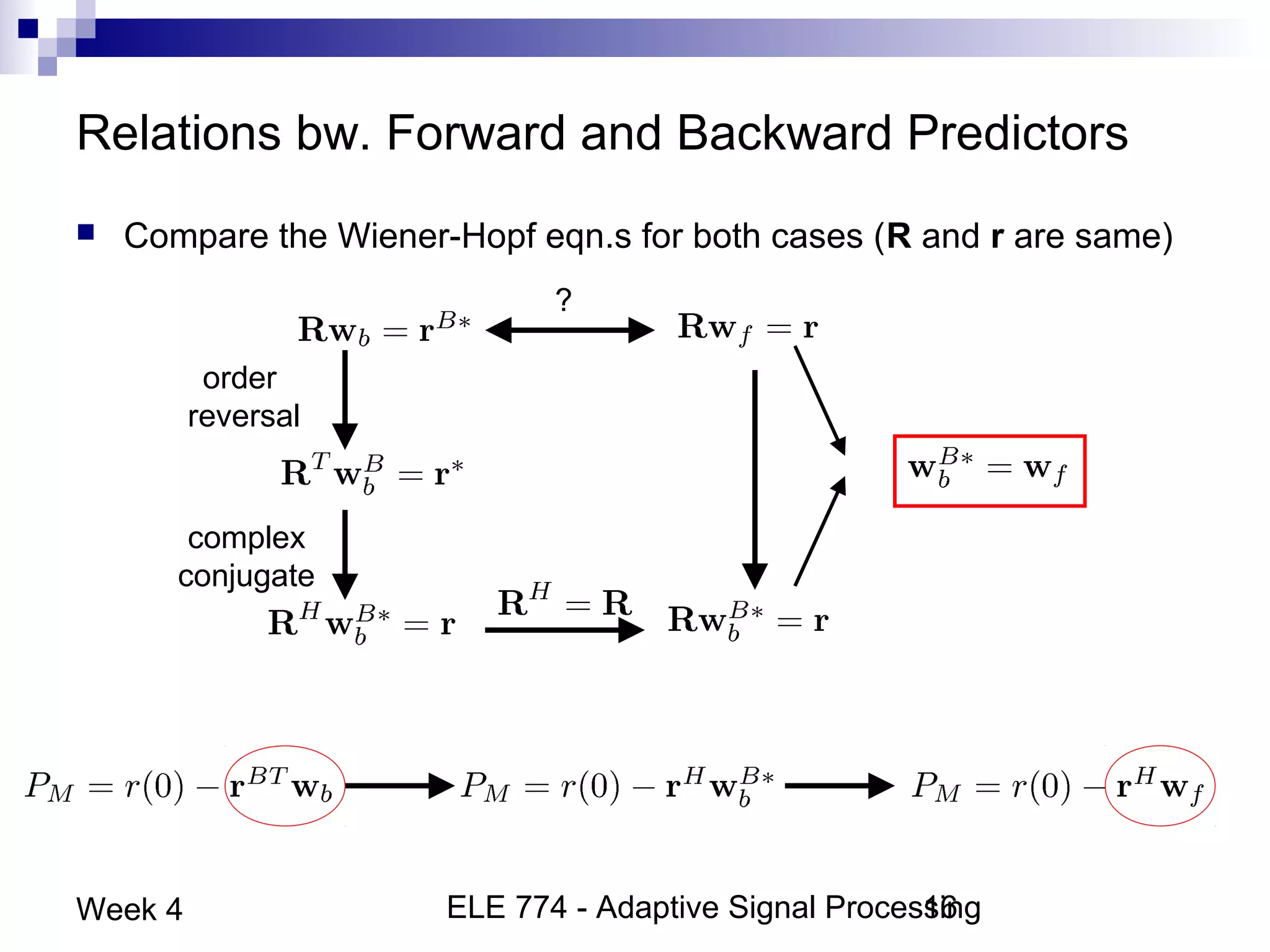
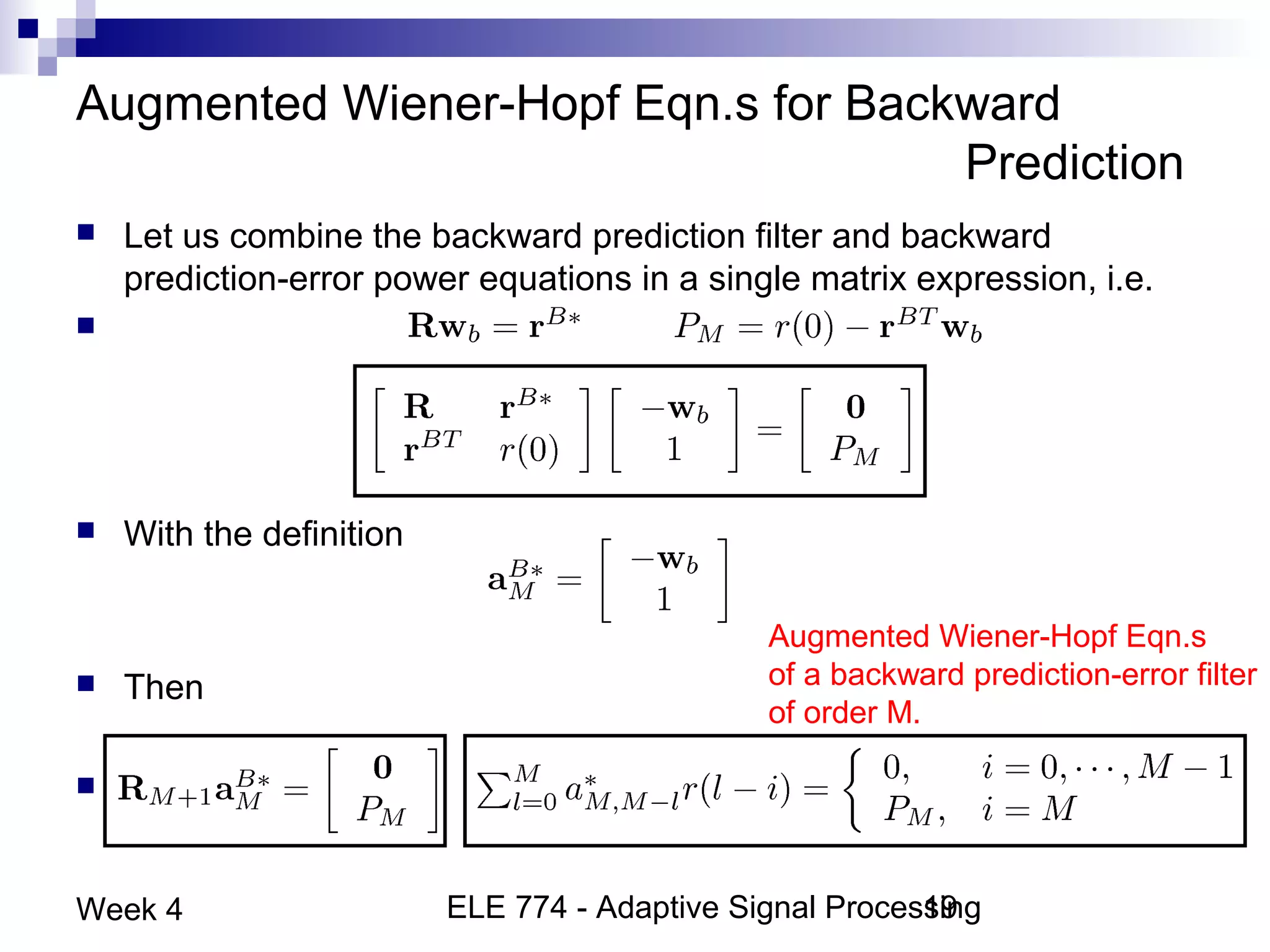
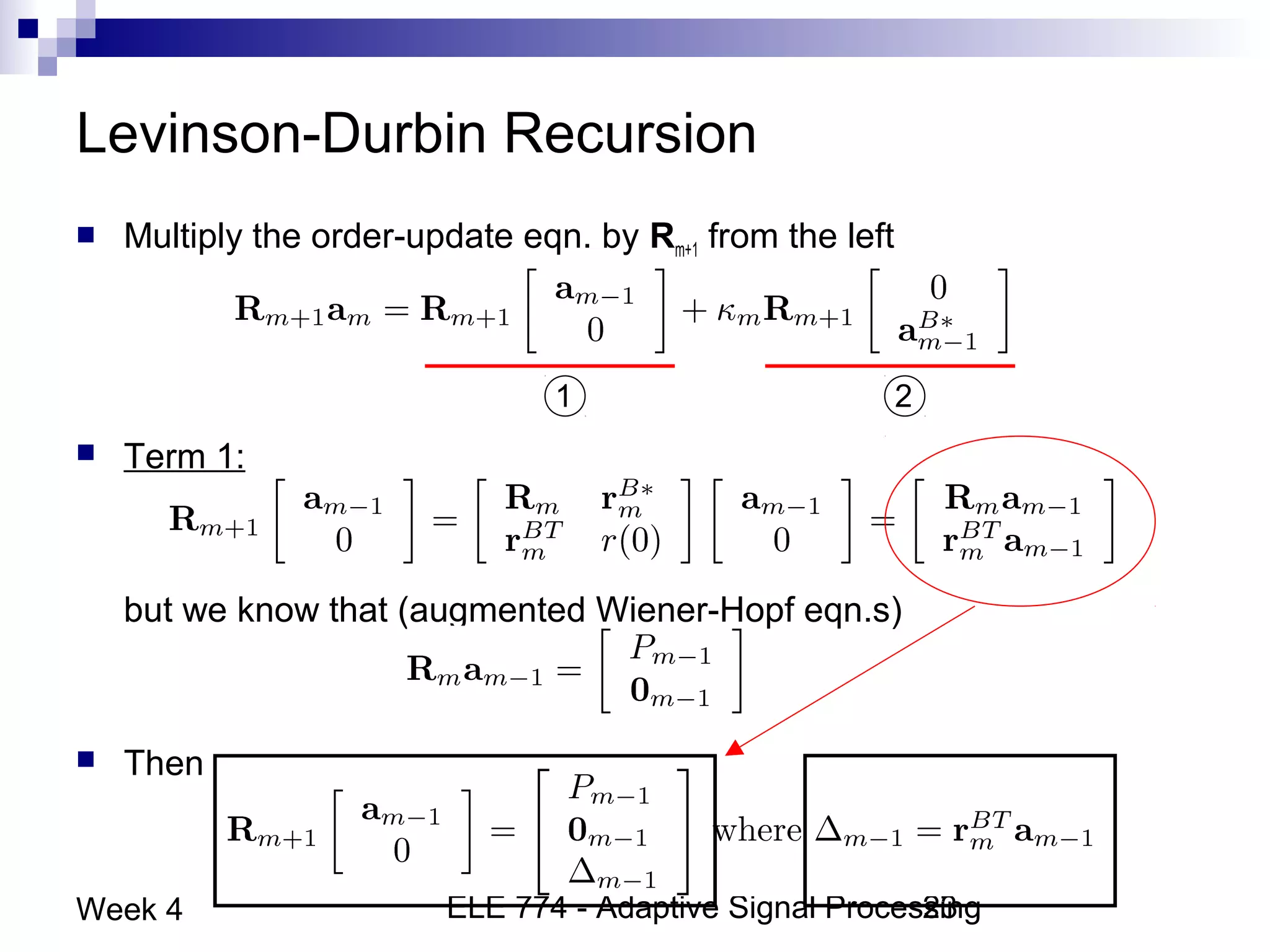
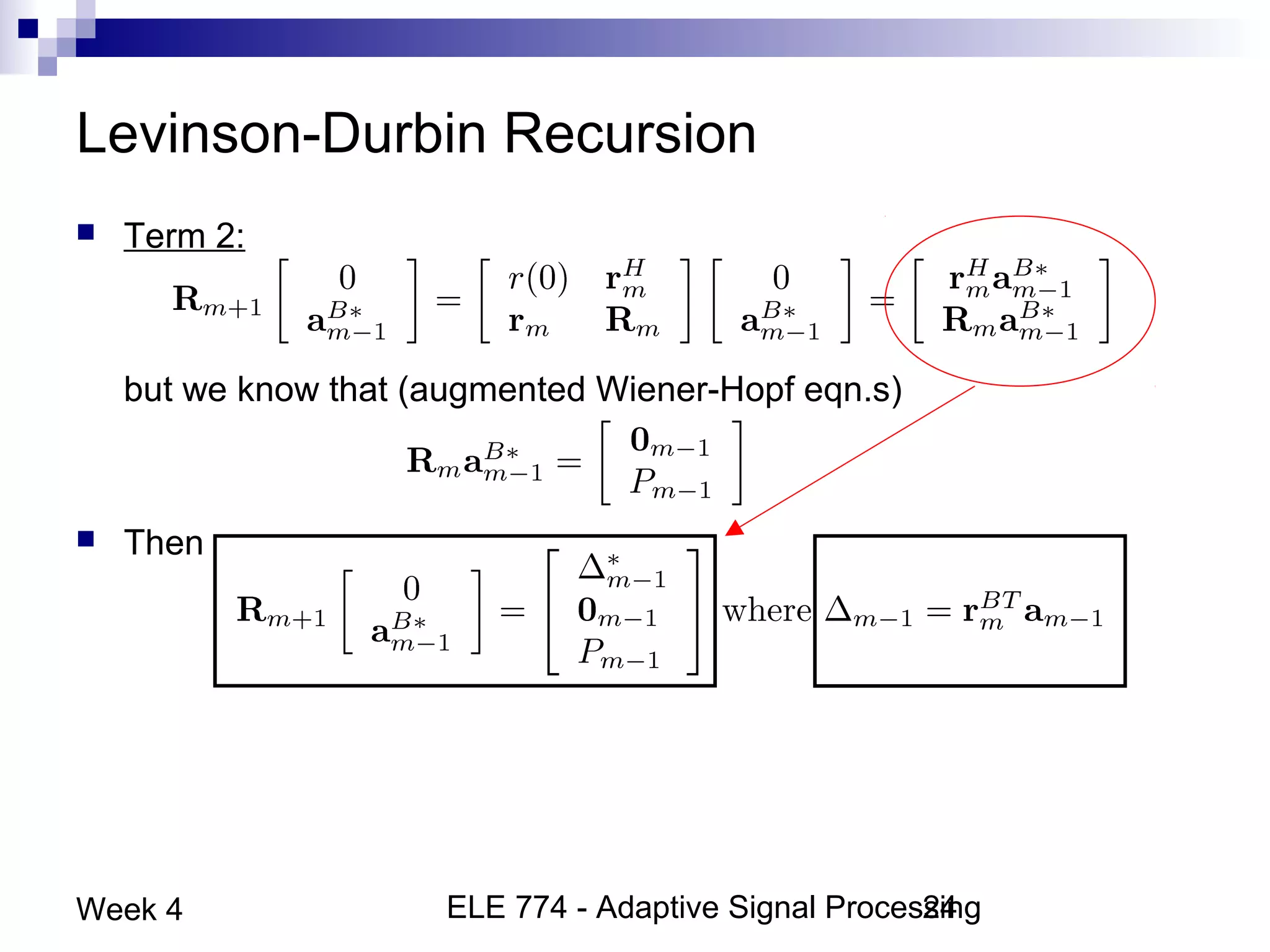
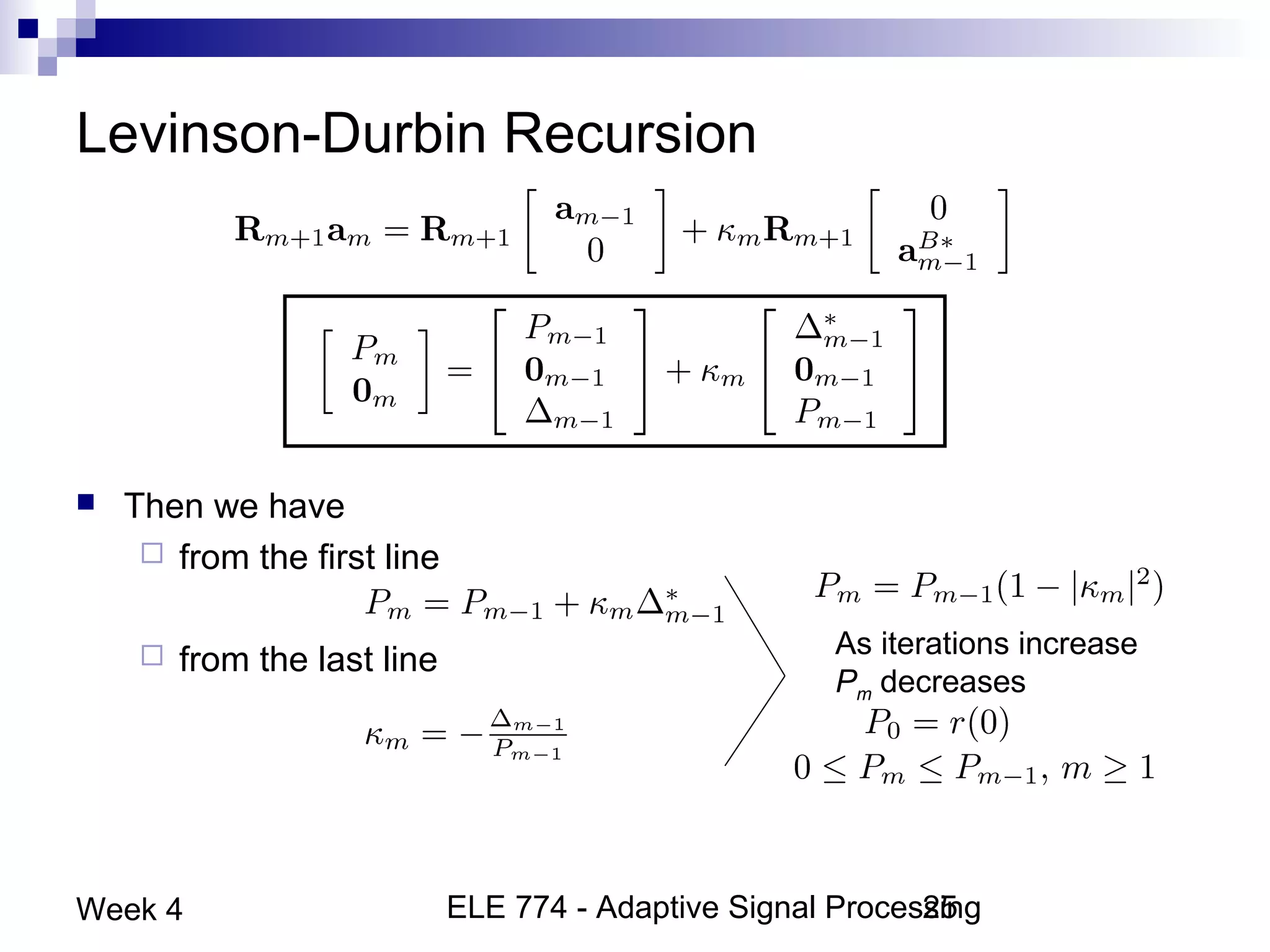
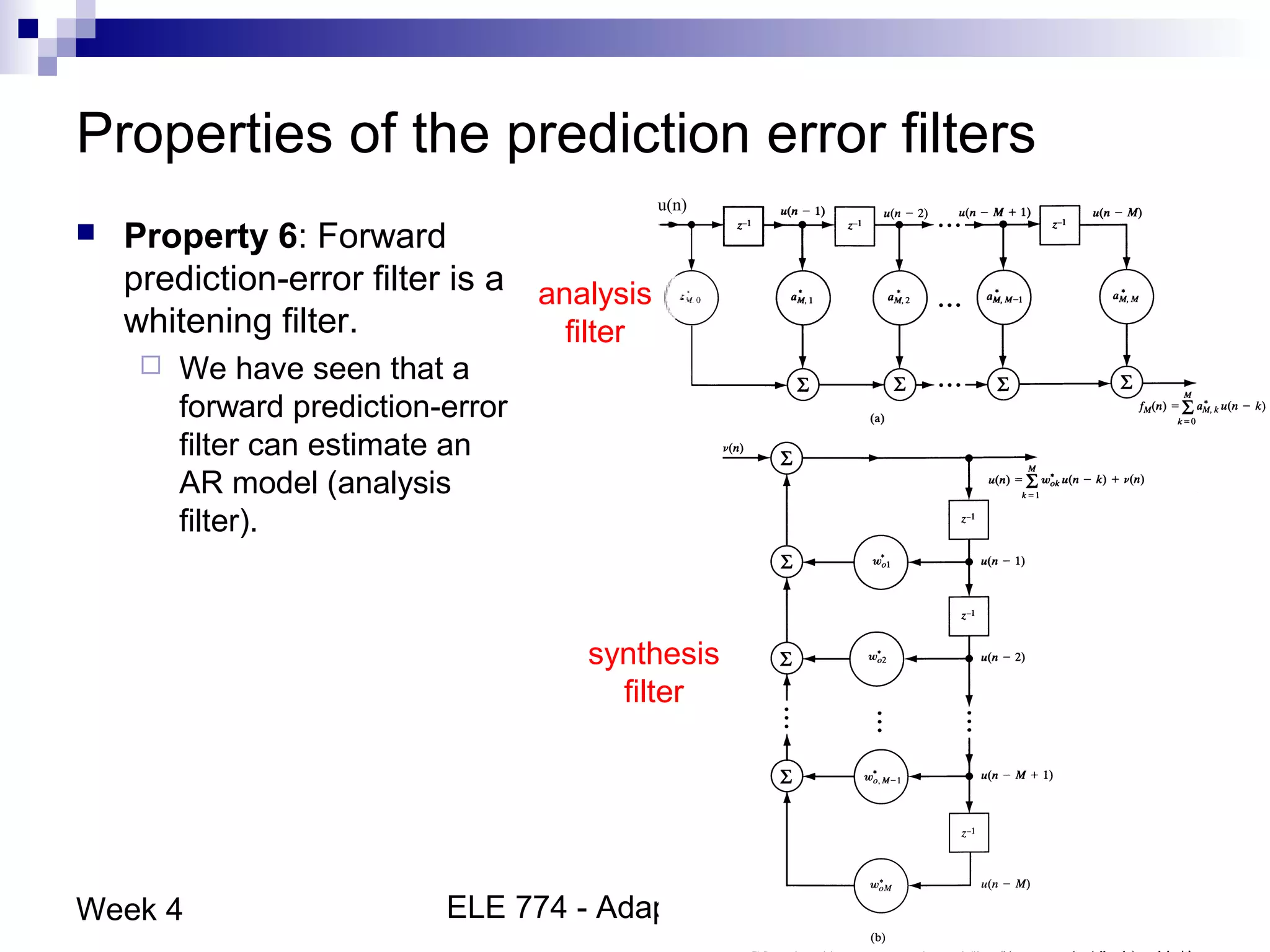
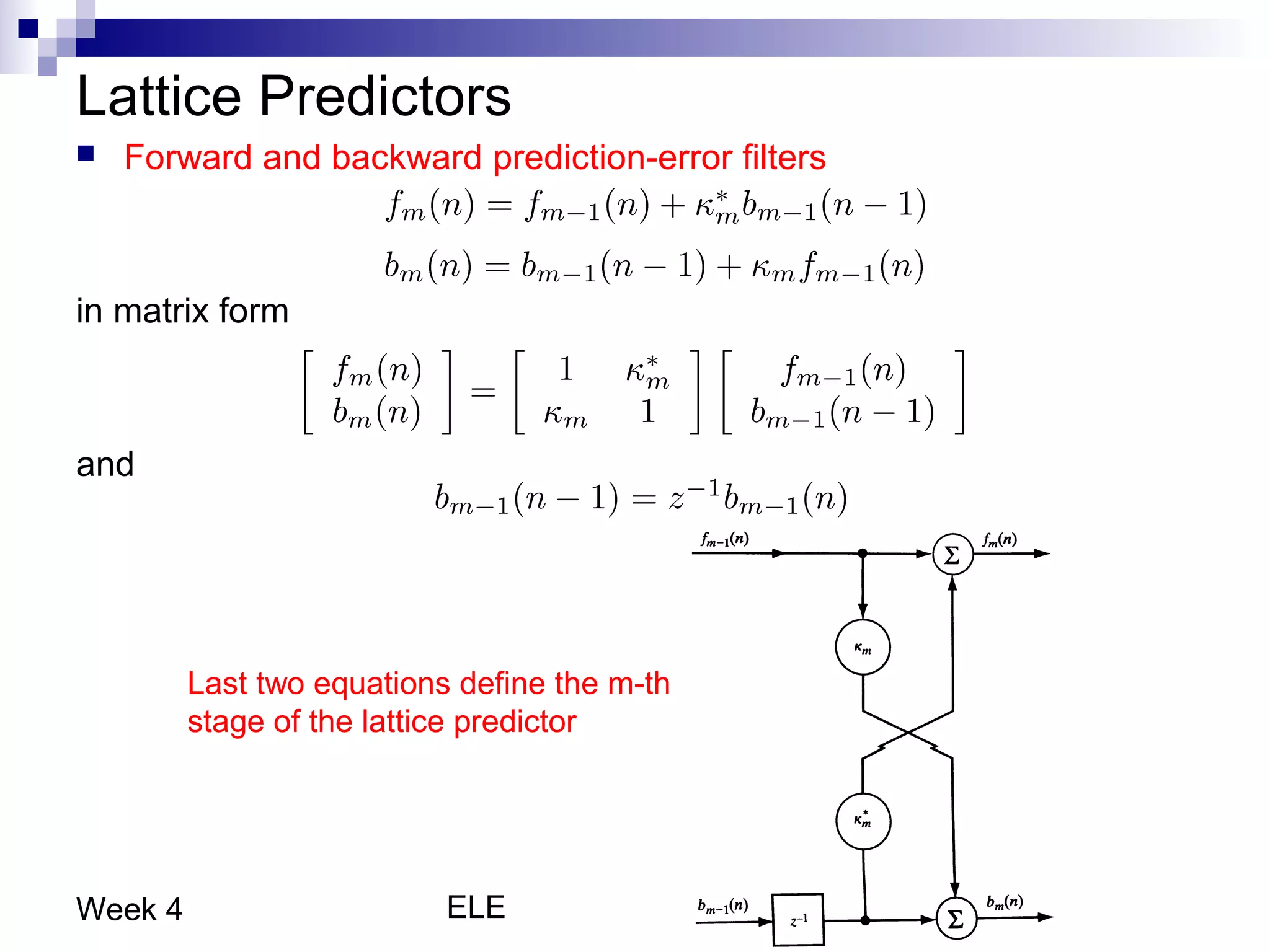
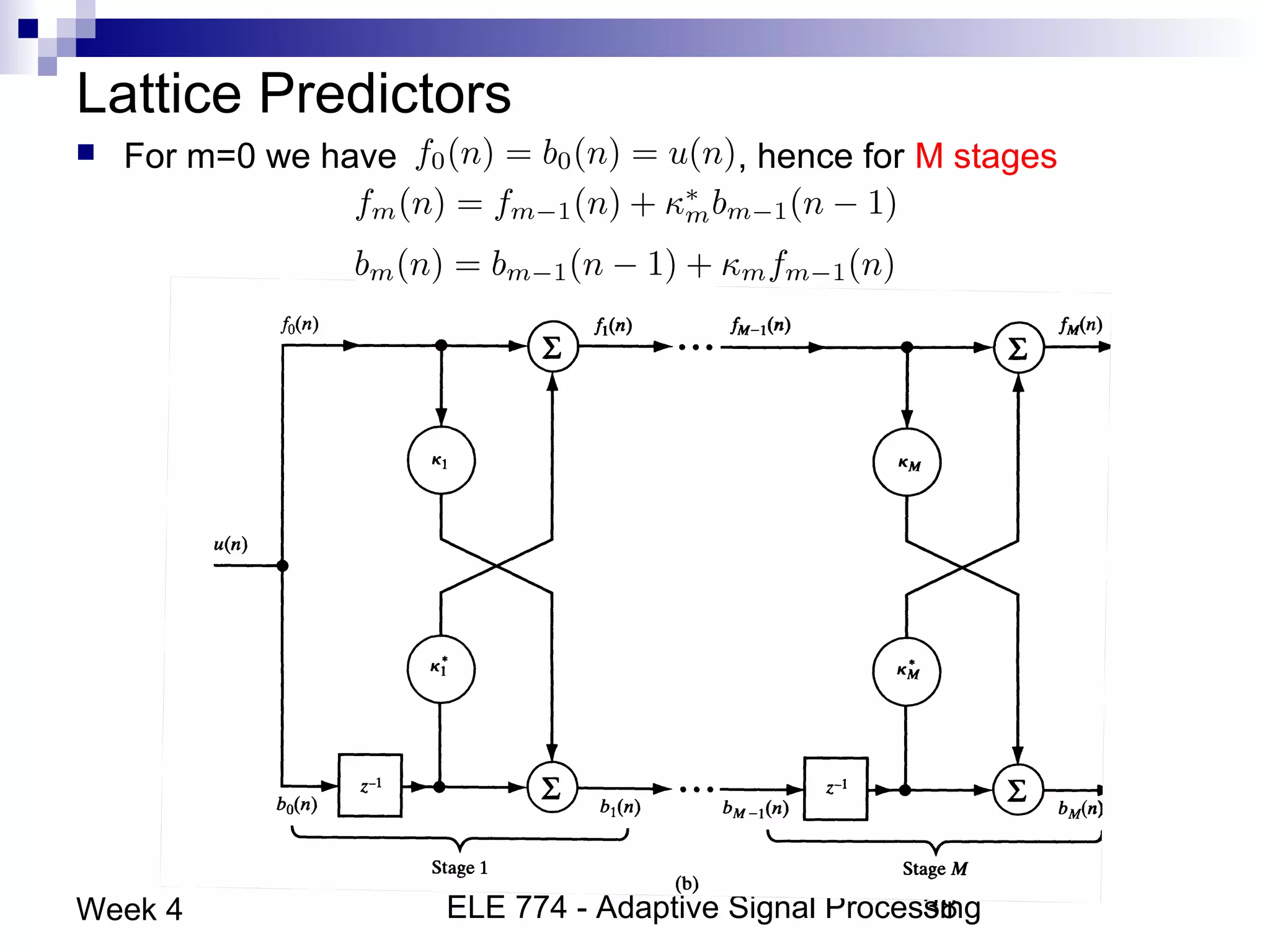
This document discusses linear prediction techniques including forward and backward prediction. It describes how to calculate the predictor filter coefficients using the Wiener-Hopf equations and how to solve them recursively using the Levinson-Durbin algorithm. This allows computing high-order predictor filters with low computational complexity. The properties of forward and backward prediction error filters are also covered, showing their relationship to autoregressive modeling and whitening filters. Lattice predictors are introduced as an efficient implementation of linear prediction filters.

1. Week 4 ELE 774 - Adaptive Signal Processing 1
LINEAR PREDICTION

2. ELE 774 - Adaptive Signal Processing2Week 4
Linear Prediction
 Problem:
 Forward Prediction
 Observing
 Predict
 Backward Prediction
 Observing
 Predict

3. ELE 774 - Adaptive Signal Processing3Week 4
Forward Linear Prediction
 Problem:
 Forward Prediction
 Observing the past
 Predict the future
 i.e. find the predictor filter taps wf,1, wf,2,...,wf,M
?

4. ELE 774 - Adaptive Signal Processing4Week 4
Forward Linear Prediction
 Use Wiener filter theory to calculate wf,k
 Desired signal
 Then forward prediction error is (for predictor order M)
 Let minimum mean-square prediction error be

5. ELE 774 - Adaptive Signal Processing5Week 4
One-step predictor
Prediction-error
filter

6. ELE 774 - Adaptive Signal Processing6Week 4
Forward Linear Prediction
 A structure similar to Wiener filter, same approach can be used.
 For the input vector
with the autocorrelation
 Find the filter taps
where the cross-correlation bw. the filter input and the desired
response is

7. ELE 774 - Adaptive Signal Processing7Week 4
Forward Linear Prediction
 Solving the Wiener-Hopf equations, we obtain
 and the minimum forward-prediction error power becomes
 In summary,

8. ELE 774 - Adaptive Signal Processing8Week 4
Relation bw. Linear Prediction and AR Modelling
 Note that the Wiener-Hopf equations for a linear predictor is
mathematically identical with the Yule-Walker equations for the
model of an AR process.
 If AR model order M is known, model parameters can be found by
using a forward linear predictor of order M.
 If the process is not AR, predictor provides an (AR) model
approximation of order M of the process.

9. ELE 774 - Adaptive Signal Processing9Week 4
Forward Prediction-Error Filter
 We wrote that
 Let
 Then

10. ELE 774 - Adaptive Signal Processing10Week 4
Augmented Wiener-Hopf Eqn.s for Forward
Prediction
 Let us combine the forward prediction filter and forward prediction-
error power equations in a single matrix expression, i.e.
and
 Define the forward prediction-error filter vector
 Then
or
Augmented Wiener-Hopf Eqn.s
of a forward prediction-error filter
of order M.

11. ELE 774 - Adaptive Signal Processing11Week 4
Example – Forward Predictor (order M=1)
 For a forward predictor of order M=1
 Then
where
 But a1,0=1, then

12. ELE 774 - Adaptive Signal Processing12Week 4
Backward Linear Prediction
 Problem:
 Forward Prediction
 Observing the future
 Predict the past
 i.e. find the predictor filter taps wb,1, wb,2,...,wb,M
?

13. ELE 774 - Adaptive Signal Processing13Week 4
Backward Linear Prediction
 Desired signal
 Then backward prediction error is (for predictor order M)
 Let minimum-mean square prediction error be

14. ELE 774 - Adaptive Signal Processing14Week 4
Backward Linear Prediction
 Problem:
 For the input vector
with the autocorrelation
 Find the filter taps
where the cross-correlation bw. the filter input and the desired
response is

15. ELE 774 - Adaptive Signal Processing15Week 4
Backward Linear Prediction
 Solving the Wiener-Hopf equations, we obtain

 and the minimum forward-prediction error power becomes
 In summary,

16. ELE 774 - Adaptive Signal Processing16Week 4
Relations bw. Forward and Backward Predictors
 Compare the Wiener-Hopf eqn.s for both cases (R and r are same)
order
reversal
complex
conjugate
?

17. ELE 774 - Adaptive Signal Processing17Week 4
Backward Prediction-Error Filter
 We wrote that
 Let
 Then
but we found that
Then

18. ELE 774 - Adaptive Signal Processing18Week 4
Backward Prediction-Error Filter
 For stationary inputs, we may change a forward prediction-error filter
into the corresponding backward prediction-error filter by reversing
the order of the sequence and taking the complex conjugation of
them.
forward prediction-error filter
backward prediction-error filter

19. ELE 774 - Adaptive Signal Processing19Week 4
Augmented Wiener-Hopf Eqn.s for Backward
Prediction
 Let us combine the backward prediction filter and backward
prediction-error power equations in a single matrix expression, i.e.
 and
 With the definition
 Then
 or
Augmented Wiener-Hopf Eqn.s
of a backward prediction-error filter
of order M.

20. ELE 774 - Adaptive Signal Processing20Week 4
Levinson-Durbin Algorithm
 Solve the following Wiener-Hopf eqn.s to find the predictor coef.s
 One-shot solution can have high computation complexity.
 Instead, use an (order)-recursive algorithm
 Levinson-Durbin Algorithm.
 Start with a first-order (m=1) predictor and at each iteration
increase the order of the predictor by one up to (m=M).
 Huge savings in computational complexity and storage.

21. ELE 774 - Adaptive Signal Processing21Week 4
Levinson-Durbin Algorithm
 Let the forward prediction error filter of order m be represented by
the (m+1)x1
and its order reversed and complex conjugated version (backward
prediction error filter) be
 The forward-prediction error filter can be order-updated by
 The backward-prediction error filter can be order-updated by
where the constant κm is called the reflection coefficient.

22. ELE 774 - Adaptive Signal Processing22Week 4
Levinson-Durbin Recursion
 How to calculate am and κm?
 Start with the relation bw. correlation matrix Rm+1 and the forward-
error prediction filter am.
 We have seen how to partition the correlation matrix
indicates order
indicates dim. of matrix/vector

23. ELE 774 - Adaptive Signal Processing23Week 4
Levinson-Durbin Recursion
 Multiply the order-update eqn. by Rm+1 from the left
 Term 1:
but we know that (augmented Wiener-Hopf eqn.s)
 Then
1 2

24. ELE 774 - Adaptive Signal Processing24Week 4
Levinson-Durbin Recursion
 Term 2:
but we know that (augmented Wiener-Hopf eqn.s)
 Then

25. ELE 774 - Adaptive Signal Processing25Week 4
Levinson-Durbin Recursion
 Then we have
 from the first line
 from the last line As iterations increase
Pm decreases

26. ELE 774 - Adaptive Signal Processing26Week 4
Levinson-Durbin Recursion - Interpretations
 κm: reflection coef.s due to the analogy with the reflection coef.s
corresponding to the boundary bw. two sections in transmission lines
 The parameter Δm represents the crosscorrelation bw. the forward
prediction error and the delayed backward prediction error
 Since f0(n)= b0(n)= u(n)
final value of the prediction error power
HW: Prove this!

27. ELE 774 - Adaptive Signal Processing27Week 4
Application of the Levinson-Durbin Algorithm
 Find the forward prediction error filter coef.s am,k, given the
autocorrelation sequence {r(0), r(1), r(2)}
 m=0
 m=1
 m=M=2

28. ELE 774 - Adaptive Signal Processing28Week 4
Properties of the prediction error filters
 Property 1: There is a one-to-one correspondence bw. the two sets
of quantities {P0, κ1, κ2, ... ,κM} and {r(0), r(1), ..., r(M)}.
 If one set is known the other can directly be computed by:

29. ELE 774 - Adaptive Signal Processing29Week 4
Properties of the prediction error filters
 Property 2a: Transfer function of a forward prediction error filter
 Utilizing Levinson-Durbin recursion
but we also have
 Then

30. ELE 774 - Adaptive Signal Processing30Week 4
Properties of the prediction error filters
 Property 2b: Transfer function of a backward prediction error filter
 Utilizing Levinson-Durbin recursion
 Given the reflection coef.s κm and the transfer functions of the
forward and backward prediction-error filters of order m-1, we can
uniquely calculate the corresponding transfer functions for the
forward and backward prediction error filters of order m.

31. ELE 774 - Adaptive Signal Processing31Week 4
Properties of the prediction error filters
 Property 3: Both the forward and backward prediction error filters have the
same magnitude response
 Property 4: Forward prediction-error filter is minimum-phase.
 causal and has stable inverse.
 Property 5: Backward prediction-error filter is maximum-phase.
 non-causal and has unstable inverse.

32. ELE 774 - Adaptive Signal Processing32Week 4
Properties of the prediction error filters
 Property 6: Forward
prediction-error filter is a
whitening filter.
 We have seen that a
forward prediction-error
filter can estimate an
AR model (analysis
filter).
u(n)
synthesis
filter
analysis
filter

33. ELE 774 - Adaptive Signal Processing33Week 4
Properties of the prediction error filters
 Property 7: Backward prediction errors are orthogonal to each
other.
( are white)
 Proof: Comes from principle of orthogonality, i.e.:
(HW: continue the proof)

34. ELE 774 - Adaptive Signal Processing34Week 4
Lattice Predictors
 A very efficient structure to implement the forward/backward
predictors.
 Rewrite the prediction error filter coef.s
 The input signal to the predictors {u(n), n(n-1),...,u(n-M)} can be
stacked into a vector
 Then the output of the predictors are
(forward) (backward)

35. ELE 774 - Adaptive Signal Processing35Week 4
Lattice Predictors
 Forward prediction-error filter
 First term
 Second term
 Combine both terms

36. ELE 774 - Adaptive Signal Processing36Week 4
Lattice Predictors
 Similarly, Backward prediction-error filter
 First term
 Second term
 Combine both terms

37. ELE 774 - Adaptive Signal Processing37Week 4
Lattice Predictors
 Forward and backward prediction-error filters
in matrix form
and
Last two equations define the m-th
stage of the lattice predictor

38. ELE 774 - Adaptive Signal Processing38Week 4
Lattice Predictors
 For m=0 we have , hence for M stages