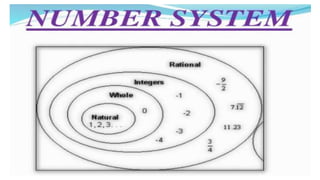
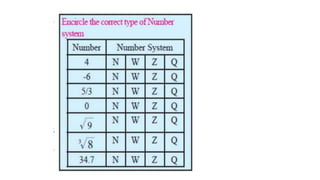
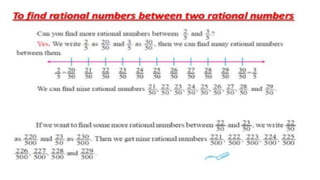
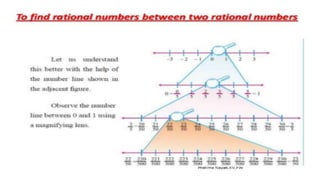
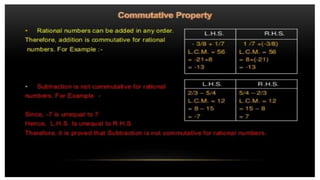
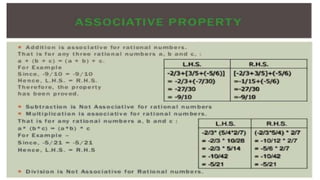
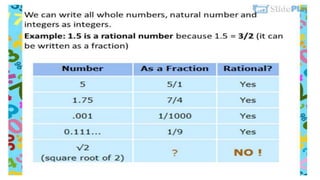
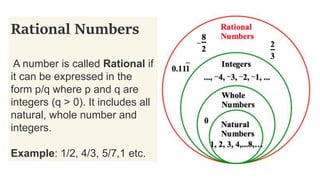
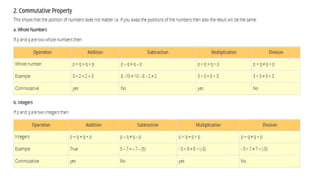
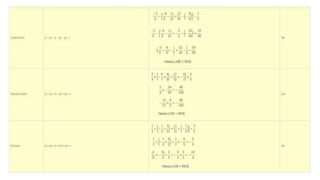
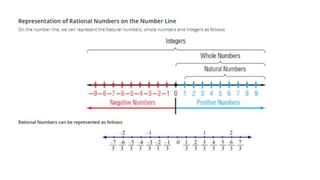
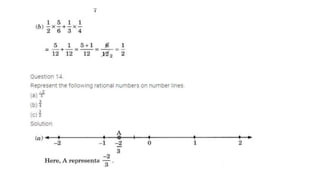
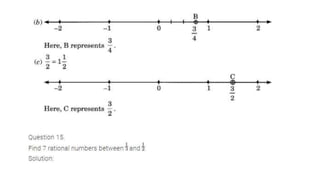
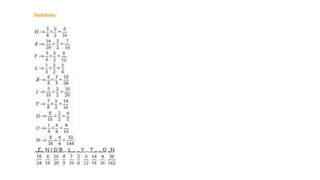
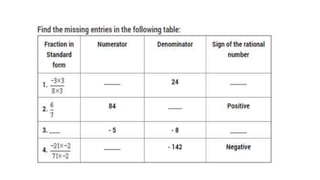
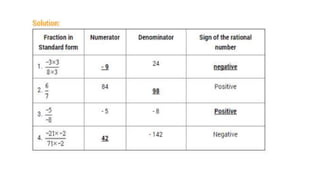
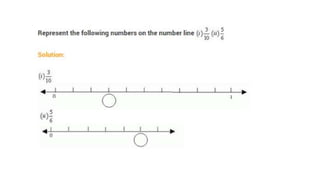
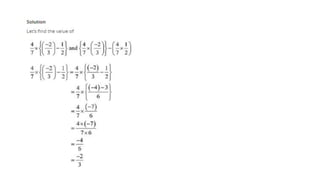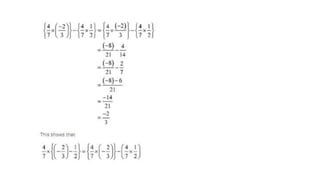The document discusses rational numbers and their properties. Rational numbers can be expressed as quotients of integers (p/q where p and q are integers and q is not zero). They include natural numbers, whole numbers, and integers. Key properties of rational numbers are that they are closed under addition and multiplication, these operations are commutative and associative, and they have additive and multiplicative identities. Rational numbers can also be represented on a number line and there are always rational numbers between any two given rational numbers.

1. PoojaK More

8. • Chapter – Rational Numbers Contents :
Introduction
Properties of Rational Numbers
Representation of Rational Numbers on the Number line.
Rational Numbers between two rational numbers.
• Learning Objectives: The students learn to represent rational numbers on the
number line. They learn to verify various properties taking different values.
•The sum of any two rational numbers is always a rational number. This is
called ‘Closure property of addition’ of rational numbers.
•Addition of two rational numbers is commutative. a/b + c/d = c/d + a/b
•Commutative property is true for addition and multiplication only
•Addition of rational numbers is associative. a/b + (c/d + e/f)= ( c/d + a/b) + e/f

9. •The rational number 0 is the additive identity for rational numbers.
•The rational number 1 is the multiplicative identity for rational number.
•The additive inverse of rational number a/b is –a/b and vice versa.
•Additive inverse of 0 is 0 itself
•The multiplicative inverse of the rational number is a/b is b/a and vice versa.
•Zero (0) has no reciprocal.
•1 and – 1 are the only rational numbers which are their own reciprocals.
•Average of two numbers always lie between that numbers

89. Rational Numbers
A number is called Rational if
it can be expressed in the
form p/q where p and q are
integers (q > 0). It includes all
natural, whole number and
integers.
Example: 1/2, 4/3, 5/7,1 etc.

90. Natural Numbers
All the positive integers from 1, 2, 3,……, ∞.
Whole Numbers
All the natural numbers including zero are called Whole Numbers.
Integers
All negative and positive numbers including zero are called Integers.
Properties of Rational Numbers
1. Closure Property
This shows that the operation of any two same types of numbers is also
the same type or not.

154. WHAT HAVE WE DISCUSSED?
1. Rational numbers are closed under the operations of
addition, subtraction and multiplication.
2. The operations addition and multiplication are (i)
commutative for rational numbers. (ii) associative for
rational numbers.
3. The rational number 0 is the additive identity for rational
numbers.
4. The rational number 1 is the multiplicative identity for
rational numbers.
5. The additive inverse of the rational number a/b is –a/b and
vice-versa.

155. 6. The reciprocal or multiplicative inverse of the rational
number a/b is c/d if a/c X b/d = 1.
7. Distributivity of rational numbers: For all rational
numbers a, b and c, a(b + c) = ab + ac and a(b – c) = ab –
ac
8. Rational numbers can be represented on a number
line.
9. Between any two given rational numbers there are
countless rational numbers. The idea of mean helps us to
find rational numbers between two rational numbers.