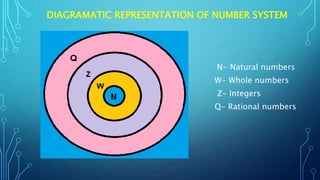
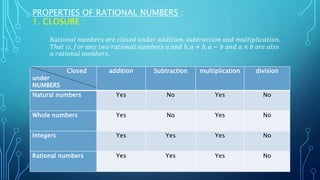
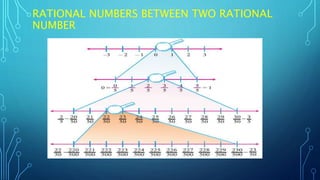
The document discusses rational numbers. It defines rational numbers as numbers that can be expressed as fractions p/q where p and q are integers and q ≠ 0. The objectives are to identify different types of numbers, know properties of rational numbers, and represent and find rational numbers on the number line. It covers the properties of rational numbers including closure, commutativity, associativity, and distributivity. It also discusses concepts like reciprocal, negative, and finding rational numbers between two given rational numbers.

2. OBJECTIVES:
• Students will be able to identify and differentiate different types
of numbers.
• Students will be able to know different properties of rational
numbers.
• Students will be able to represent the rational numbers on the
number line.
• Students will be able to find rational numbers between any two
rational numbers.

3. RATIONAL NUMBERS
• The numbers which can be expressed in the form of
𝑝
𝑞
, where 𝑝
and 𝑞 are integers and 𝑞 ≠ 0 are called as rational numbers.
• 𝑒. 𝑔.
2
3
, 5,
100
555
, 0, 2.4 etc.

4. TYPE OF NUMBERS:
• Natural Numbers: All counting numbers are called as natural
numbers.
e.g. 2, 35, 111, 1234 etc.
• Whole Numbers: Collection of all natural numbers with zero is
known as whole numbers.
e.g. 0, 2, 45, 234, 2947 etc.
• Integers: Collection of all natural numbers with its negative
numbers and zero is known as integers.
e.g. 56, -23, 0, -357, 6789 etc.

5. DIAGRAMATIC REPRESENTATION OF NUMBER SYSTEM
N- Natural numbers
W- Whole numbers
Z- Integers
Q- Rational numbers

6. PROPERTIES OF RATIONAL NUMBERS :
1. CLOSURE :
R𝑎𝑡𝑖𝑜𝑛𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠 𝑎𝑟𝑒 𝑐𝑙𝑜𝑠𝑒𝑑 𝑢𝑛𝑑𝑒𝑟 𝑎𝑑𝑑𝑖𝑡𝑖𝑜𝑛, 𝑠𝑢𝑏𝑡𝑟𝑎𝑐𝑡𝑖𝑜𝑛 𝑎𝑛𝑑 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑎𝑡𝑖𝑜𝑛.
Tℎ𝑎𝑡 𝑖𝑠, 𝑓𝑜𝑟 𝑎𝑛𝑦 𝑡𝑤𝑜 𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠 𝑎 𝑎𝑛𝑑 𝑏, 𝑎 + 𝑏, 𝑎 − 𝑏 𝑎𝑛𝑑 𝑎 × 𝑏 𝑎𝑟𝑒 𝑎𝑙𝑠𝑜
𝑎 𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠.
Closed
under
NUMBERS
addition Subtraction multiplication division
Natural numbers Yes No Yes No
Whole numbers Yes No Yes No
Integers Yes Yes Yes No
Rational numbers Yes Yes Yes No

7. 2. COMMUTATIVITY:
𝑂𝑛𝑙𝑦 𝑎𝑑𝑑𝑖𝑡𝑖𝑜𝑛 𝑎𝑛𝑑 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑎𝑡𝑖𝑜𝑛 𝑎𝑟𝑒 𝑐𝑜𝑚𝑚𝑢𝑡𝑎𝑡𝑖𝑣𝑒 𝑓𝑜𝑟 𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠.
𝑇ℎ𝑎𝑡 𝑖𝑠 𝑓𝑜𝑟 𝑎𝑛𝑦 𝑡𝑤𝑜 𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠 𝑎 𝑎𝑛𝑑 𝑏, 𝑎 + 𝑏 = 𝑏 + 𝑎 𝑎𝑛𝑑 𝑎 × 𝑏 = 𝑏 × 𝑎.
Commutative
for
NUMBERS
addition subtraction multiplication division
Natural numbers Yes No Yes No
Whole numbers Yes No Yes No
Integers Yes No Yes No
Rational numbers Yes No Yes No

8. 3. ASSOCIATIVITY:
𝑂𝑛𝑙𝑦 𝑎𝑑𝑑𝑖𝑡𝑖𝑜𝑛 𝑎𝑛𝑑 𝑚𝑢𝑙𝑡𝑖𝑝𝑙𝑖𝑐𝑎𝑡𝑖𝑜𝑛 𝑎𝑟𝑒 𝑎𝑠𝑠𝑜𝑐𝑖𝑎𝑡𝑖𝑣𝑒 𝑓𝑜𝑟 𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠.
𝑇ℎ𝑎𝑡 𝑖𝑠 𝑓𝑜𝑟 𝑎𝑛𝑦 𝑡ℎ𝑟𝑒𝑒 𝑟𝑎𝑡𝑖𝑜𝑛𝑎𝑙 𝑛𝑢𝑚𝑏𝑒𝑟𝑠 𝑎, 𝑏 𝑎𝑛𝑑 𝑐, 𝑎 + 𝑏 + 𝑐 = 𝑎 + 𝑏 + 𝑐 𝑎𝑛𝑑
𝑎 × 𝑏 × 𝑐 = 𝑎 × 𝑏 × 𝑐.
Associative
for
NUMBERS
addition subtraction multiplication division
Natural numbers Yes No Yes No
Whole numbers Yes No Yes No
Integers Yes No Yes No
Rational numbers Yes No Yes No

9. 4. DISTRIBUTIVITY OF MULTIPLICATION OVER
ADDITION:
• 𝑎 × 𝑏 + 𝑐 = 𝑎 × 𝑏 + (𝑎 × 𝑐)
where a, b and c are rational numbers.
e.g.
−2
3
×
4
6
+
−2
9
=
−2
3
×
12 + −4
18
=
−2
3
×
8
18
=
−16
54
=
−8
27
−2
3
×
4
6
=
−8
18
=
−4
9
−2
3
×
−2
9
=
4
27
Therefore
−2
3
×
4
6
+
−2
3
×
−2
9
=
−4
9
+
4
27
=
−8
27
Thus,
−2
3
×
4
6
+
−2
9
=
−2
3
×
4
6
+
−2
3
×
−2
9

10. THE ROLE OF ZERO:
• Zero is called the identity for the addition of rational numbers.
It is the additive identity for integers and whole numbers as
well.
e.g. 0+2 = 2+0 = 2 𝑎 + 0 = 0 + 𝑎 = 𝑎
-5+0 = 0+(-5) = -5 where 𝑎 is any rational number
4
8
+ 0 = 0 +
4
8
=
4
8
THE ROLE OF ONE:
• 1 is the multiplicative identity for rational numbers, integers
and whole numbers.
e.g. 6 × 1 = 1 × 6 = 6 𝑎 × 1 = 1 × 𝑎 = 𝑎
−5
8
× 1 = 1 ×
−5
8
=
−5
8
where 𝑎 is any rational number

11. RECIPROCAL:
• A rational number
𝑐
𝑑
is called the reciprocal or multiplicative inverse of another
rational number
𝑎
𝑏
if
𝑎
𝑏
×
𝑐
𝑑
= 1 .
e.g.
7
9
×
9
7
= 1 and
−5
8
×
8
−5
= 1
We say that
9
7
is reciprocal of
7
9
and
8
−5
is reciprocal of
−5
8
.
NEGATIVE OF A NUMBER:
• We say that
−𝑎
𝑏
is the additive inverse of
𝑎
𝑏
and
𝑎
𝑏
is the additive inverse of
−𝑎
𝑏
as
𝑎
𝑏
+
−𝑎
𝑏
=
−𝑎
𝑏
+
𝑎
𝑏
= 0 .
2
5
+
−2
5
=
2 + −2
5
= 0
Here
−2
5
is the additive inverse of
2
5
.

12. REPRESENTATION OF RATIONAL NUMBERS ON THE
NUMBER LINE

13. RATIONAL NUMBERS BETWEEN TWO RATIONAL
NUMBER

14. • e.g. Find any ten rational number between
−5
8
and
7
10
.
Solution: We first convert
−5
8
and
7
10
to rational numbers with
same denominators.
−5
8
=
−5×5
8×5
=
−25
40
and
7
10
=
7×4
10×4
=
28
40
Thus we have
−24
40
,
−23
40
,
−22
40
,
−21
40
,
−20
40
, … . . ,
27
40
as the rational numbers
between
−5
8
and
7
10
.

15. THANK YOU
PRESENTED BY,
DEEPAK MEHER (TGT
MATHEMATICS)
KENDRIYA VIDYALAYA, BOUDH
BHUBANESWAR REGION