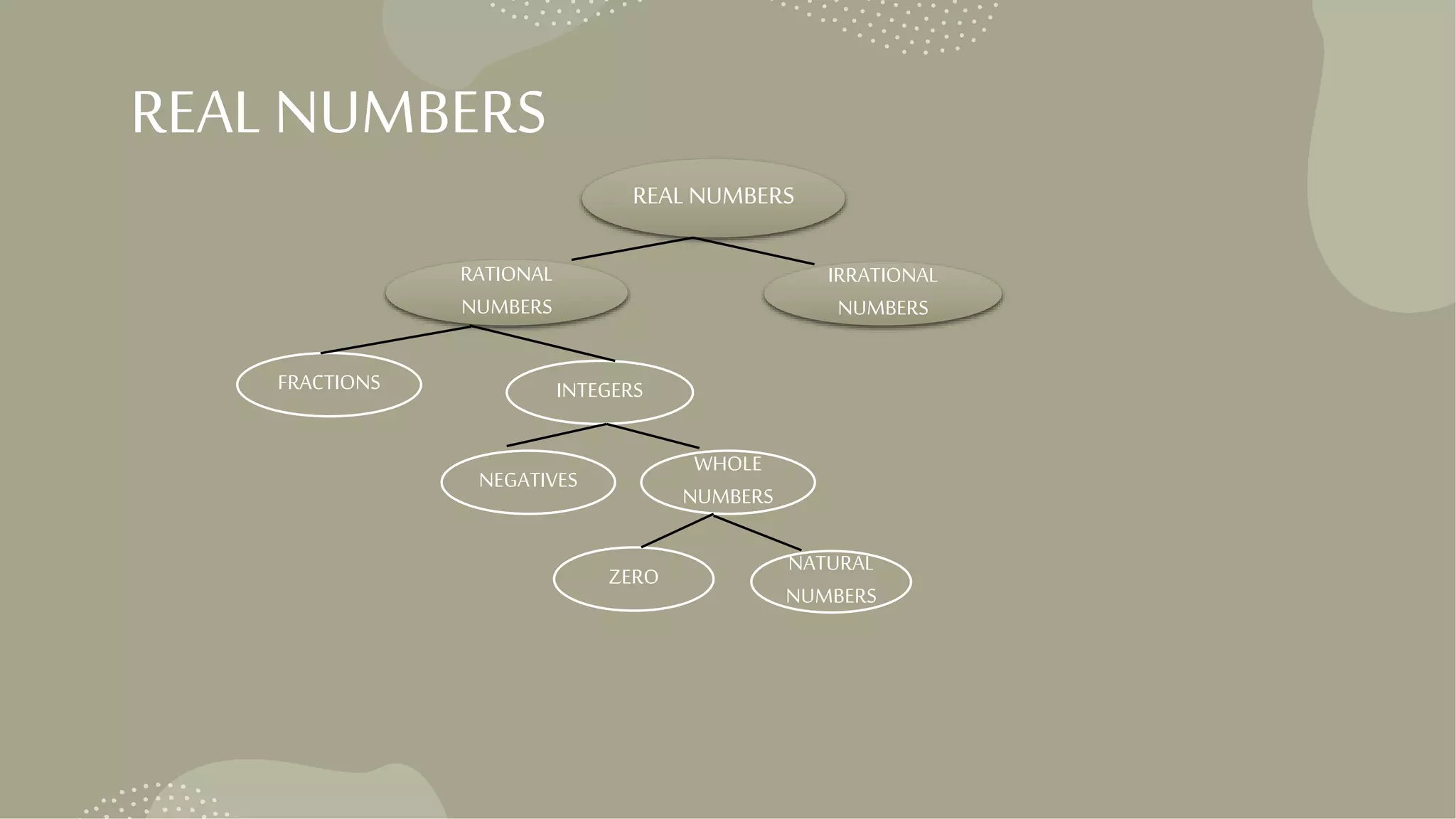
This document provides an overview of a maths project on number systems. It discusses different types of numbers including real numbers, rational numbers, irrational numbers and integers. Rational numbers are divided into fractions and integers. Integers are divided into negatives and whole numbers, with whole numbers further divided into zero and natural numbers. Irrational numbers cannot be represented as fractions, while rational numbers can. The document also covers decimal expansions, representing real numbers on a number line, laws of exponents and the process of rationalization.

1. MATHS PROJECT
NUMBERSYSTEM
Thenumber system is the system of naming or representing numbers. Forexample:
number:1,2,3,4,5… and infinity, roman numerals: I,II,V,IX…and infinity. Number system was
discovered by ARYABHATTA.

2. TOPICS COVERED
• REAL NUMBERS
• DECIMALEXPANSION
• REAL NUMBERS ON NUMBER LINE
• LAWSOF EXPONENTS
• RATIONALISATION

3. REALNUMBERS
REAL NUMBERS
RATIONAL
NUMBERS
IRRATIONAL
NUMBERS
FRACTIONS INTEGERS
NEGATIVES
WHOLE
NUMBERS
ZERO
NATURAL
NUMBERS

4. IRRATIONAL NUMBERS: Those numbers which cannot be represented in the form of p/q and q is
equal to 0.For e.g., (Pi)
RATIONAL NUMBERS: Those numbers which canbe represented inthe form of p/q (or fraction)
where p and q are integers and qis not equal to 0. For e.g.,5/1
Rationalnumbers are divided into two parts:-
• Fractions:- Fraction isa number of the form p/q, such that q is not equal to zero or one.
• Integers:- Integers are the numbers which canbe positive, negative or zero, but cannot be a
fraction.
Integers are divided into two parts :-
• Negatives:- In the real number system, a negative number is a number that is less than zero.
• Whole numbers:- The numbers which starts with 0 to infinity.
Whole numbers are divided into two parts:-
• Zero:- Zero is the integer denoted 0 that, when used asa counting number, means that no
objects are present.
• Naturalnumbers:- The numbers which starts with 1 to infinity.

5. DECIMALEXPANSION
Decimal expansion are of three types:-
i) Terminating
ii) Non-terminating, Non-repeating
iii) Repeating
i) TERMINATING:- A terminating decimal isdefined asa decimal number that contains a finite number
of digits after the decimal points. E.g.,1/4 = 0.25, Hence it’s a terminating decimal expansion.
ii)NON-TERMINATING ,NON-REPEATING:-Non-terminating decimals are the one that does not have
an end term. e.g., 7/11=0.63636363….,0.63 (when a digit is keeps on repeating we put a bar on the
repeating digit.)
iii) REPEATING:- A repeating decimal hasa decimal part containing a sequence of digits that is infinitely
repeating or non-zero.

6. REPRESENTATIONOFREALNUMBER(3.5)ON
NUMBERLINE.
1 2 3 4 5 6 7 8 9 10
3.1 3.2 3.3 3.4 3.5 3.6 3.7 3.8 3.9 4
3

7. 2 ona Number line

8. LAWS OF EXPONENT
 ap X aq = ap+q
 (ap)q= apq
 ap/aq = ap-q
 ap bp = (ab)p
For example - 22/3X 21/5
Using law of exponent: ap X aq = ap+q
22/3+1/5= 213/15

9. RATIONALIZATION
Rationalization is process by denominator isconjugated and then multiply and divide by the
denominator and numerator.
Some examples of rationalization are :-
(i) 1/(√5+√2)
Solution:
Multiply and divide 1/(√5+√2) by (√5-√2)
[1/(√5+√2)]×(√5-√2)/(√5-√2) = (√5-√2)/(√5+√2)(√5-√2)
= (√5-√2)/(√52-√22) [denominator is obtained by the property, (a+b)(a-b) = a2-b2]
= (√5-√2)/(5-2)
= (√5-√2)/3

10. PREPARED BY :-KANIKA
CLASS-9TH ‘B’
ROLL NO. 18