This document discusses rank-aware algorithms for joint sparse recovery from multiple measurement vectors (MMV). It begins by introducing the MMV problem and showing that when the rank of the signal matrix is r, the necessary and sufficient conditions for unique recovery are less restrictive than in the single measurement vector case. Classical MMV algorithms like SOMP and l1/lq minimization are not rank-aware. The document then proposes two rank-aware pursuit algorithms: 1) Rank-Aware OMP, which modifies the atom selection step of SOMP but still suffers from rank degeneration over iterations. 2) Rank-Aware Order Recursive Matching Pursuit (RA-ORMP), which forces the sparsity

1. IDCOM, University of Edinburgh
Rank Aware Algorithms for Joint Sparse
Recovery
Mike Davies*
Joint work with Yonina Eldar‡ and Jeff Blanchard†
* Institute of Digital Communications, University of Edinburgh
‡ Technion, Israel † Grinnell College, USA

2. IDCOM, University of Edinburgh
Outline of Talk
• Multiple Measurements vs Single Measurements
• Nec.+suff. conditions for Joint Sparse Recovery
• Reduced complexity combinatorial search
• Classical approaches to sparse MMV problem
– How good are SOMP and convex optimization?
• Rank Aware Pursuits
– Evolution of the rank of residual matrices
– A recovery guarantee
• Empirical simulations

3. IDCOM, University of Edinburgh
Sparse Single Measurement Vector
Problem
m x1 mxn n x1
Measurements Measurement
Matrix
Sparse Signal
k nonzero elements
Given y ∈ Rm and Φ ∈ Rm×n with m < n find:
x = argmin | supp(x)| s.t. Φx = y.
ˆ
x

4. IDCOM, University of Edinburgh
Sparse Multiple Measurement Vector
Problem
m×l m×n n×l
Measurement
Measurements Matrix
row support
Sparse Signal
k nonzero rows
Given Y ∈ Rm×l and Φ ∈ Rm×n with m < n find:
ˆ
X = argmin | supp(X)| s.t. ΦX = Y.
X

5. IDCOM, University of Edinburgh
MMV uniqueness
Worst Case
• Uniqueness of solution for sparse MMV problem is equivalent to that for
SMV problem. Simply replicate SMV problem:
X = {x, x, . . . , x}
Hence nec. + suff. condition to uniquely determine each k-sparse vector x is
given by SMV condition:
spark(Φ)
| supp(X)| = k <
2
Rank 'r' Case
• If Rank(Y)=r then the necessary + sufficient conditions are less restrictive
[Chen & Huo 2006, D. & Eldar 2010]:
spark(Φ) − 1 + rank(Y)
| supp(X)| = k <
2
Equivalently we can replace rank(Y) with rank(X).
More measurements (higher rank) makes recovery easier!

6. IDCOM, University of Edinburgh
MMV uniqueness
Generic scenario:
Typical matrices achieve maximal spark:
Φ ∈ Rm×n → spark(Φ) = m + 1
Typical matrices achieve maximal rank
X ∈ Rk×l → rank(X) = r = min{k, l}
Hence generically we have uniqueness if
m ≥ 2k − min{k, l} + 1 ≥ k + 1
When l ≥ k we typically only need k+1 measurements

7. IDCOM, University of Edinburgh
Exhaustive search solution
How does the rank change the exhaustive search?
SMV exhaustive search:
find , | | = k s.t. ΦX = Y
However since span(Y) ⊂ span(Φ ) and rank(Y) = r
∃γ⊂ , |γ| = k − r s.t. span([Φγ , Y ]) = span(Φ )
n
In fact we have a reduced k−r+1 combinatorial search.

8. IDCOM, University of Edinburgh
Geometric Picture for MMV
φ1 φ2 Y = ΦΛ XΛ,:
φ3
2−sparse vector ∈ span(Y )
span(Y )
If X is k-sparse and rank(Y) = r there exists a (k-r+1)-sparse vector in span(Y)

9. IDCOM, University of Edinburgh
Maximal Rank Exhaustive Search: MUSIC
When we have maximal rank(X) = k the exhaustive search is linear and
can be solved with a modified MUSIC algorithm.
Let U = orth(Y) This is an orthonormal basis for span(Φ )
Then under identifiablity conditions we have:
(I − UUT )φi 2 = 0, if and only if i ∈ .
(in practice select support by thresholding)
Theorem 1 (Feng 1996) Let Y = ΦX with | supp(X)| = k, rank(X) = k
ˆ
and k < spark(Φ) − 1. Then MUSIC is guaranteed to recover X (i.e. X = X).

10. IDCOM, University of Edinburgh
Maximal rank problem is not NP-hard
Furthermore there is no constraint on
n!

11. IDCOM, University of Edinburgh
Popular MMV solutions

12. IDCOM, University of Edinburgh
Popular MMV sparse recovery solutions
Two classes of MMV sparse recovery algorithm:
greedy, e.g.
Algorithm 1 Simultaneous Orthogonal Matching Pursuit (SOMP)
1: initialization: R(0) = Y, X(0) = 0, 0 = ∅
2: for n = 1; n := n + 1 until stopping criterion do
3: in = argmaxi φT R(n−1) q
i
n n−1 n
4: = ∪i
(n) †
5: X n ,: = Φ n Y
6: R(n) = P ⊥(n) Y where P ⊥(n) := (I − Φ (n) Φ† (n) )
7: end for
and relaxed, e.g.
Algorithm 2 ℓ1 /ℓq Minimization
ˆ
X = argmin ||X||1,q s.t. ΦX = Y
X

13. IDCOM, University of Edinburgh
Do such MMV solutions exploit the
rank?
Answer: NO. [D. & Eldar 2010]
Theorem 2 (SOMP is not rank aware) Let τ be given such that 1 ≤ τ ≤ k
and suppose that
max ||Φ† φj ||1 > 1
j∈
for some support , | | = k. Then there exists an X with supp(X) = and
rank(X) = τ that SOMP cannot recover.
SMV OMP Exact
Recovery condition
Proof - Rank r perturbation of rank 1 problem approaches rank 1 recovery
property due to continuity norm.

14. IDCOM, University of Edinburgh
Do such MMV solutions exploit the
rank?
Answer: NO. [D. & Eldar 2010]
Theorem 3 (ℓ1 /ℓq minimization is not rank aware) Let τ be given such
that 1 ≤ τ ≤ k and suppose that there exists a z ∈ N (Φ) such that
||z ||1 > ||z c ||1
for some support , | | = k. Then there exists an X with supp(X) = ,
rank(X) l=Null
SMV 1 τ that the mixed norm solution cannot recover.
Space Property
Proof - Rank r perturbation of rank 1 problem approaches rank 1 recovery
property due to continuity of norm.

15. IDCOM, University of Edinburgh
Rank Aware Pursuits

16. IDCOM, University of Edinburgh
Rank Aware Selection
Aim: to select individual atoms in a similar manner to modified MUSIC
Rank Aware Selection [D. & Eldar 2010]
At the nth iteration make the following selection:
(n) (n−1)
= ∪ argmax ||φT U(n−1) ||2
i
i
where U(n−1) = orth(R(n−1) )
Properties:
1. Worst case behaviour does not approach SMV case.
2. When rank(R) = k it always selects a correct atom as with
MUSIC

17. IDCOM, University of Edinburgh
Rank Aware OMP
Rank Aware OMP
Let's simply replace the selection step in SOMP with the rank aware
selection.
Does this provide guaranteed recovery in the full rank scenario?
Answer: NO.
Why?
We get rank degeneration of the residual matrix:
rank(R(i) ) ≤ min{rank(Y ), k − i}
As we take more steps the rank reduces to one while R(i) is typically still
k-sparse.
We lose the rank benefits as we iterate

18. IDCOM, University of Edinburgh
Rank Aware Order Recursive Matching
Pursuit
The fix...
We can fix this problem by forcing the sparsity to also reduce as a
function of iteration. This is achieved by:
Algorithm 1 Rank Aware Order Recursive Matching Pursuit (RA-ORMP)
1: Initialize R(0) = Y, X(0) = 0, 0 = ∅, P ⊥ = I
(0)
2: for n = 1; n := n + 1 until stopping criterion do
3: Calculate orthonormal basis for residual: U(n−1) = Orth(R(n−1) )
4: in = argmaxi∈ (n−1) φT U(n−1) 2 / P ⊥
i (n−1) φi 2
n
5: = n−1 ∪ in
(n)
6: X n ,: = Φ† n Y
7: R(n) = P ⊥(n) Y where P ⊥ := (I − Φ
(n) (n) Φ† (n) )
8: end for
˜
R(n)is (k-n)-sparse in the modified dictionary φi = P ⊥(n) φi / P ⊥(n) φi 2

19. IDCOM, University of Edinburgh
RA-OMP vs RA-ORMP
Comparison of how (typical) residual rank (–) and sparsity (–)
evolve as a function of iteration
RA-OMP RA-ORMP
k k
r r
k k
iteration # iteration #
- region where correct selection is not guaranteed

20. IDCOM, University of Edinburgh
SOMP/RA-OMP/RA-ORMP
Comparison
SOMP RA−OMP RA=ORMP
1 1 1
Prob of Exact Recovery
Prob of Exact Recovery
Prob of Exact Recovery
0.8 0.8 0.8
0.6 0.6 0.6
0.4 0.4 0.4
0.2 0.2 0.2
0 0 0
0 10 20 30 0 10 20 30 0 10 20 30
Sparsity k Sparsity k Sparsity k
n = 256, m = 32, l = 1,2,4,8,16,32. Dictionary ~ i.i.d. Gaussian and X
coefficients ~ Gaussian i.i.d. (note that this is beneficial to SOMP!)

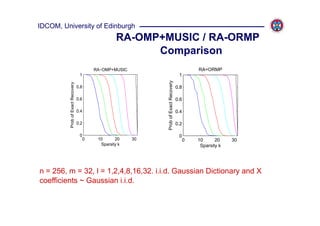
21. IDCOM, University of Edinburgh
Rank Aware OMP
Alternative Solutions
Recently two independent solutions have been proposed that are variations on
a theme:
1. Compressive MUSIC [Kim et al 2010]
i. perform SOMP for k-r-1 steps but SOMP is rank blind
ii. apply modified MUSIC
2. Iterative MUSIC [Lee & Bresler 2010]
1. orthogonalize: U = orth(Y ) orthogonalization is not
2. apply SOMP to {Φ, U } for k-r-1 steps guaranteed beyond step 1
3. apply modified MUSIC
This motivates us to consider a minor modification of (2):
3 RA-OMP+MUSIC
i. perform RA-OMP for k-r-1 steps
ii. apply modified MUSIC

22. IDCOM, University of Edinburgh
Recovery guarantee
Two nice rank aware solutions
a) Apply RA-OMP for k-r-1 steps then complete with modified MUSIC
b) Apply RA-ORMP for k steps (if first k-r steps make correct selection we
have guaranteed recovery)
we now have the following recovery guarantee [Blanchard & D.]:
Theorem 4 (MMV CS recovery) Assume XΛ ∈ Rn×r is in general position
for some support set Λ, |Λ| = k > r and let Φ is a random matrix independent
of X, Φi,j ∼ N (0, m−1 ). Then (a) and (b) can recover X from Y with high
probability if:
log N
m ≥ const.k +1
r
That is: as r increases the effect of the log N term diminishes

23. IDCOM, University of Edinburgh
RA-OMP+MUSIC / RA-ORMP
Comparison
RA−OMP+MUSIC RA=ORMP
1 1
Prob of Exact Recovery
Prob of Exact Recovery
0.8 0.8
0.6 0.6
0.4 0.4
0.2 0.2
0 0
0 10 20 30 0 10 20 30
Sparsity k Sparsity k
n = 256, m = 32, l = 1,2,4,8,16,32. i.i.d. Gaussian Dictionary and X
coefficients ~ Gaussian i.i.d.

24. IDCOM, University of Edinburgh
Empirical Phase Transitions
RA−OMP+MUSIC 16 16
RA−ORMPl l= 16=
RA−OMP = 16 l
SOMP l =
50
45
40
35
30
m
25
20
15
10
5
5 10 15 20 25 30 35 40 45 50
k
Gaussian dictionary "phase transitions" with Gaussian
significant coefficients

25. IDCOM, University of Edinburgh
Correlated vs uncorrelated
coefficients
SOMP RA-ORMP
SOMP l = 16 RA−ORMP l = 16
50 50
45 45
40 40
35 35
30 30
m
m
25 25
20 20
15 15
10 10
5 5
5 10 15 20 25 30 35 40 45 50 5 10 15 20 25 30 35 40 45 50
k k
Gaussian dictionary "phase transitions" with uncorrelated
sparse coefficients

26. IDCOM, University of Edinburgh
Correlated vs uncorrelated
coefficients
SOMP RA-ORMP
SOMP l = 16, highly correlated RA−ORMP l = 16 highly correlated
50 50
45 45
40 40
35 35
30 30
m
m
25 25
20 20
15 15
10 10
5 5
5 10 15 20 25 30 35 40 45 50 5 10 15 20 25 30 35 40 45 50
k k
Gaussian dictionary "phase transitions" with highly correlated
sparse coefficients

27. IDCOM, University of Edinburgh
Summary
• MMV problem is easier than SMV problem in general
• Don't dismiss using exhaustive search (not always NP-hard!)
• Good rank aware greedy algorithms exist
Questions
• Can we extend these ideas to IHT or CoSaMP?
• How can we incorporate rank awareness into convex optimization?

28. IDCOM, University of Edinburgh
Workshop : Signal Processing with Adaptive Sparse
Structured Representations (SPARS '11)
June 27-30, 2011 - Edinburgh, (Scotland, UK)
Plenary speakers :
David L. Donoho, Stanford University, USA
Martin Vetterli, EPFL, Switzerland
Stephen J. Wright, University of Wisconsin, USA
David J. Brady, Duke University, Durham, USA
Yi Ma, University of Illinois at Urbana-Champaign, USA
Joel Tropp, California Institute of Technology, USA
Remi Gribonval, Centre de Recherche INRIA Rennes, France
Francis Bach, Laboratoire d'Informatique de l'E.N.S., France