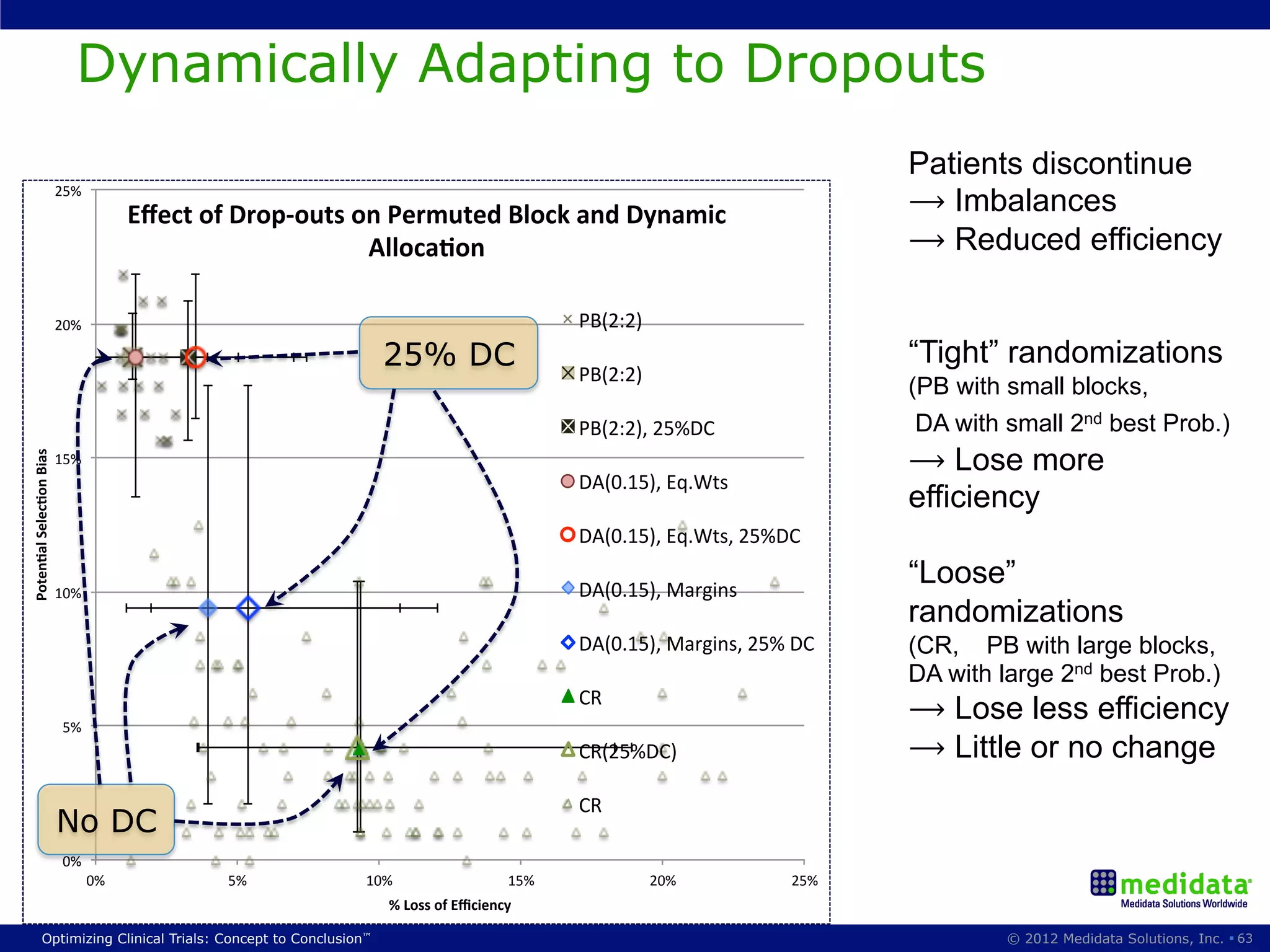
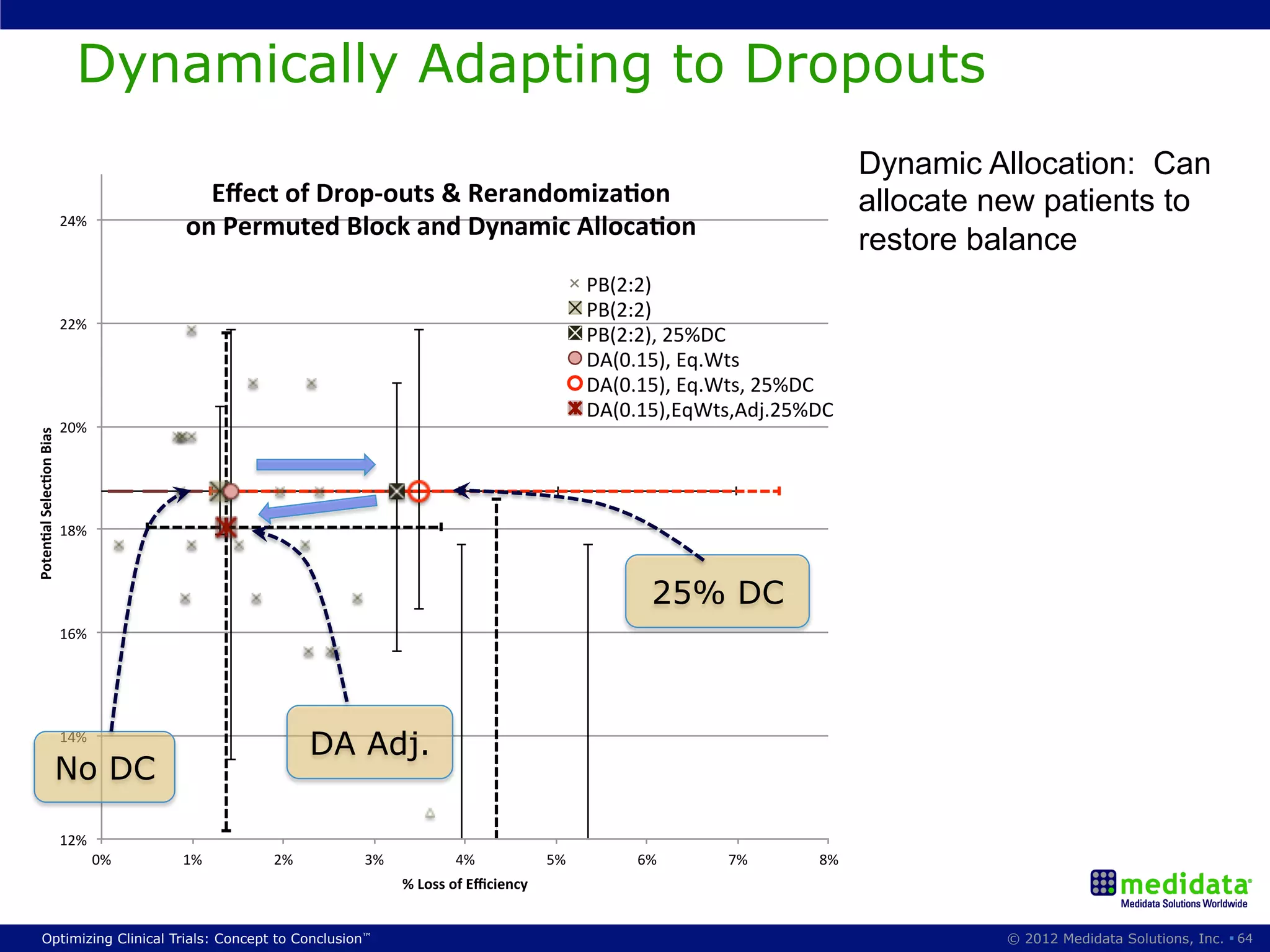
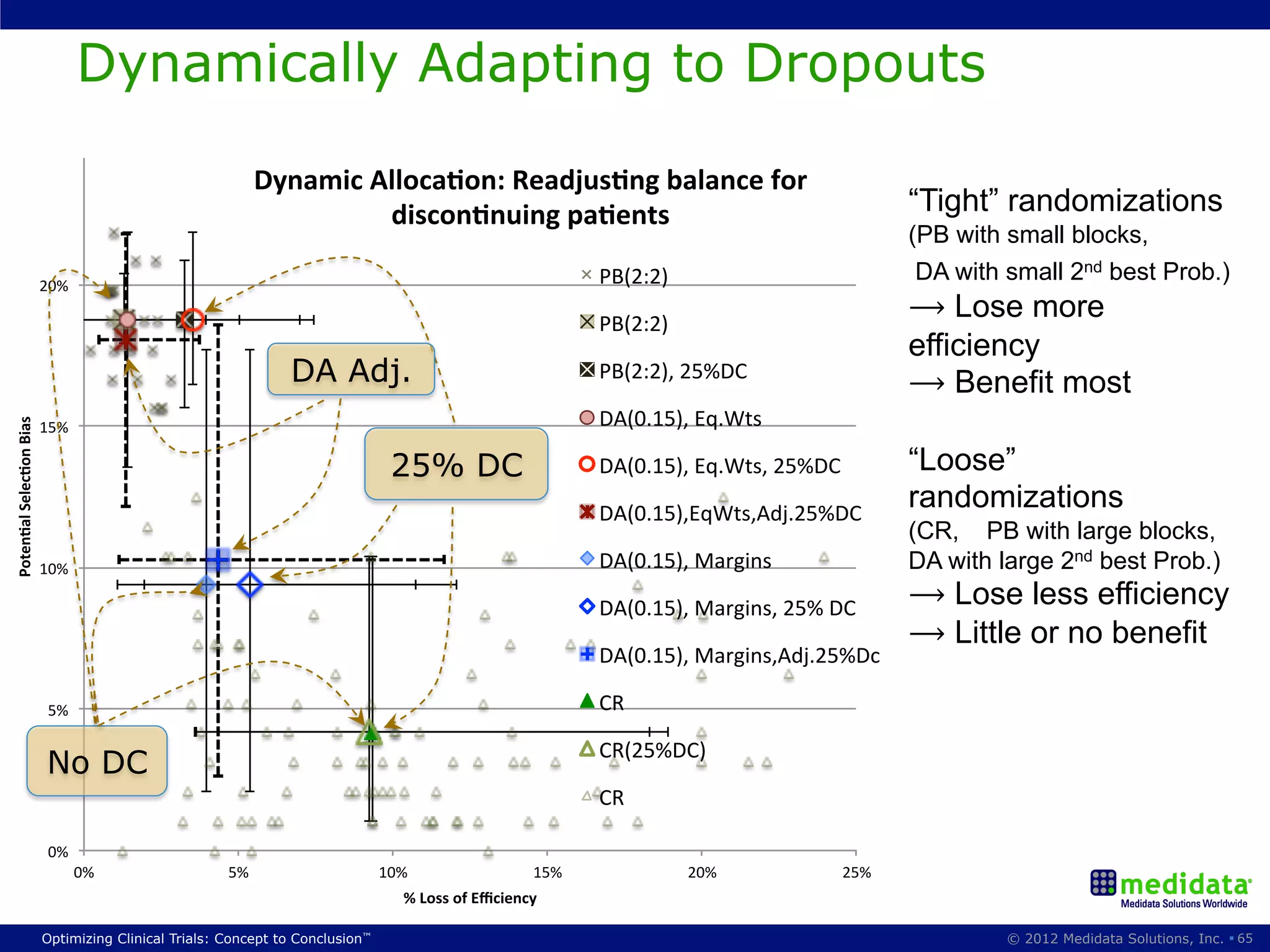
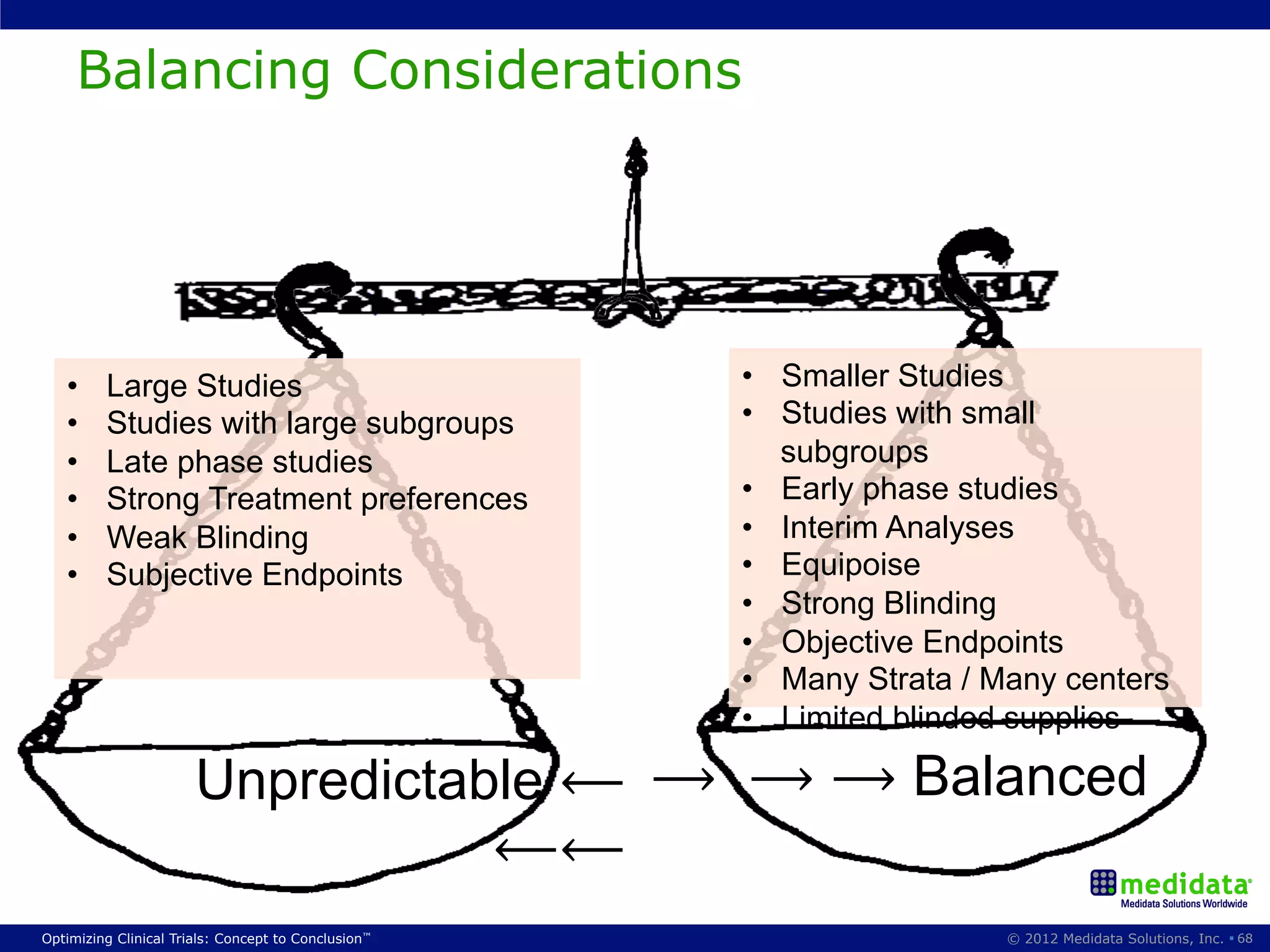
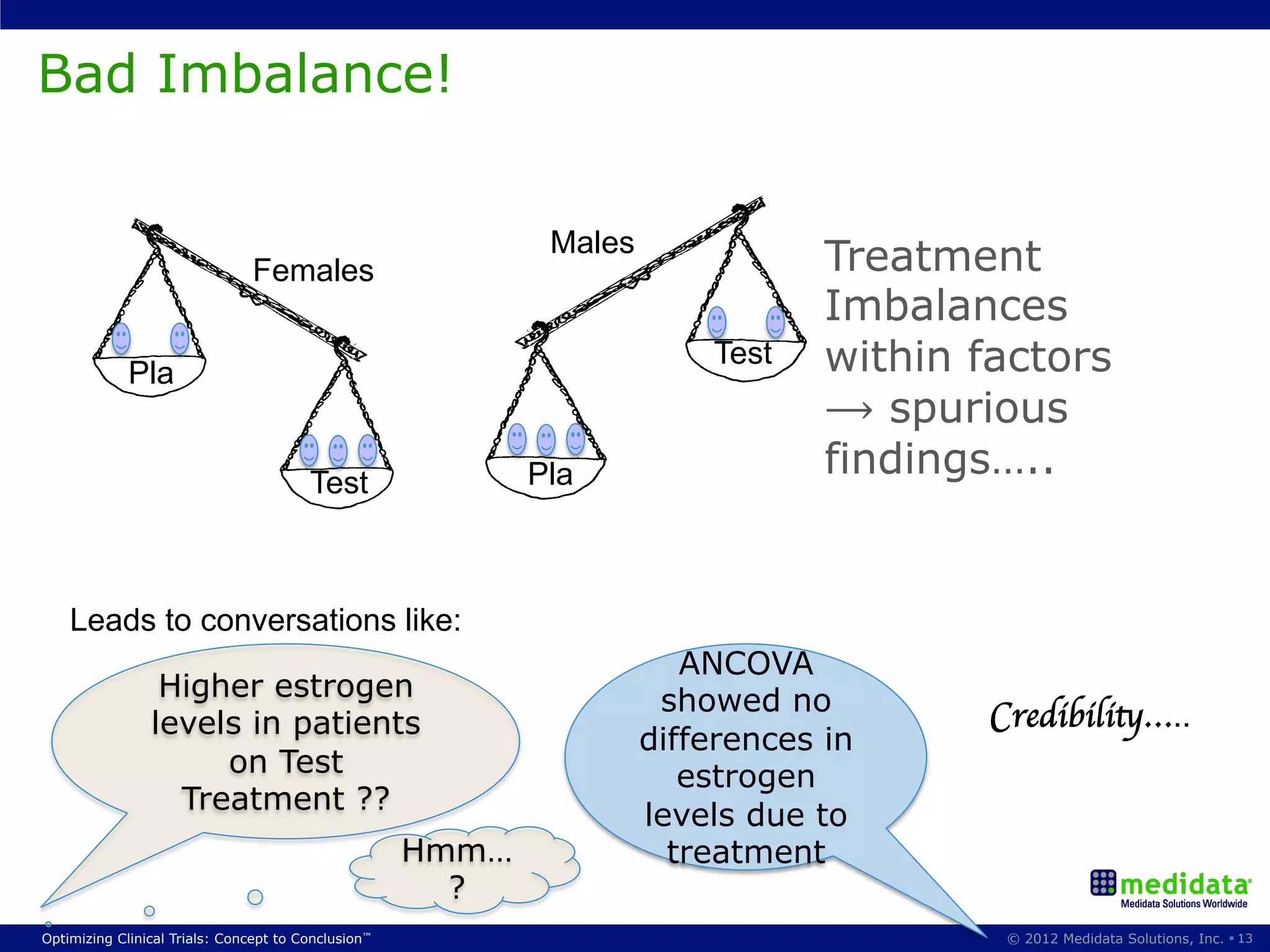
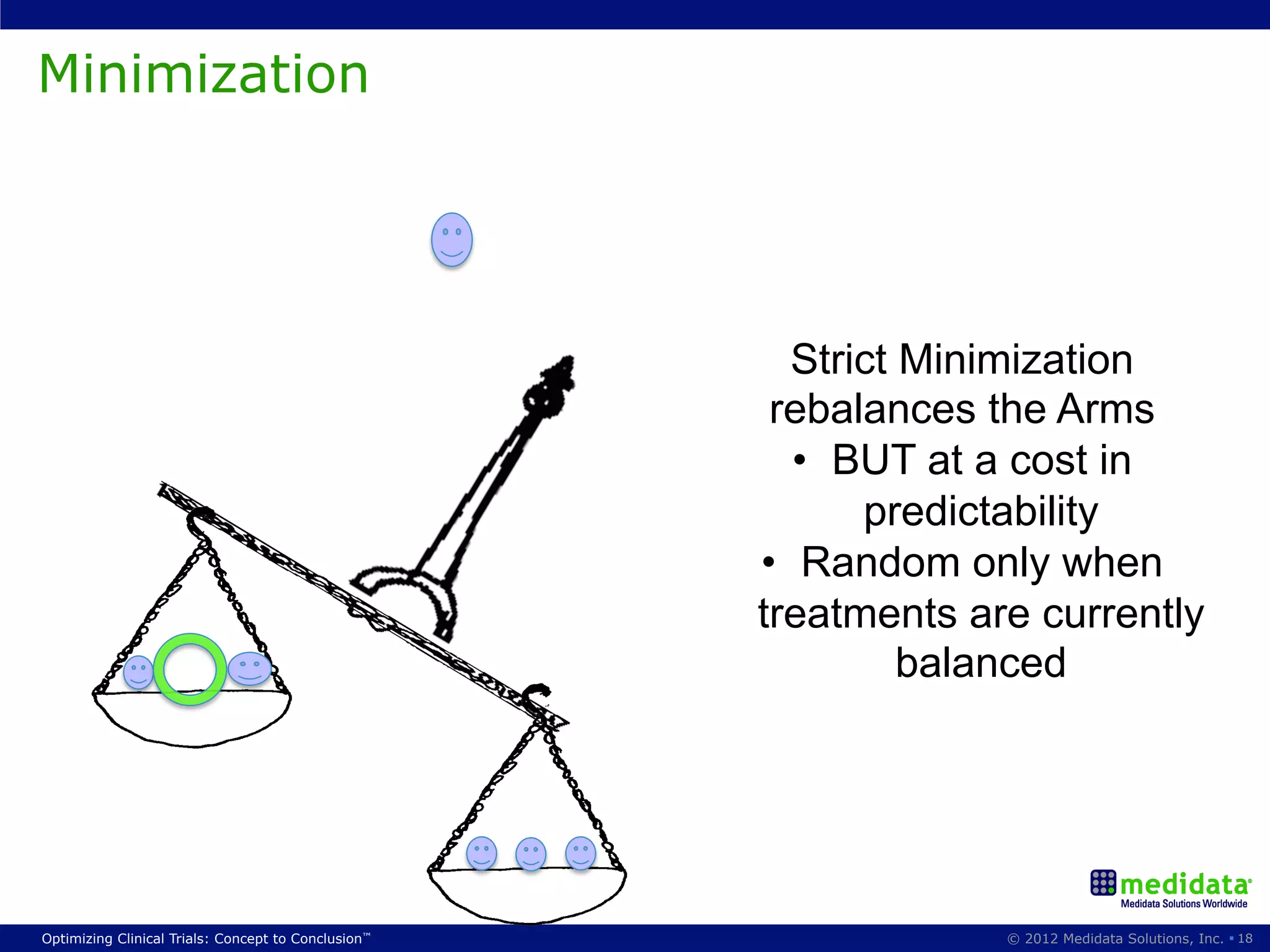
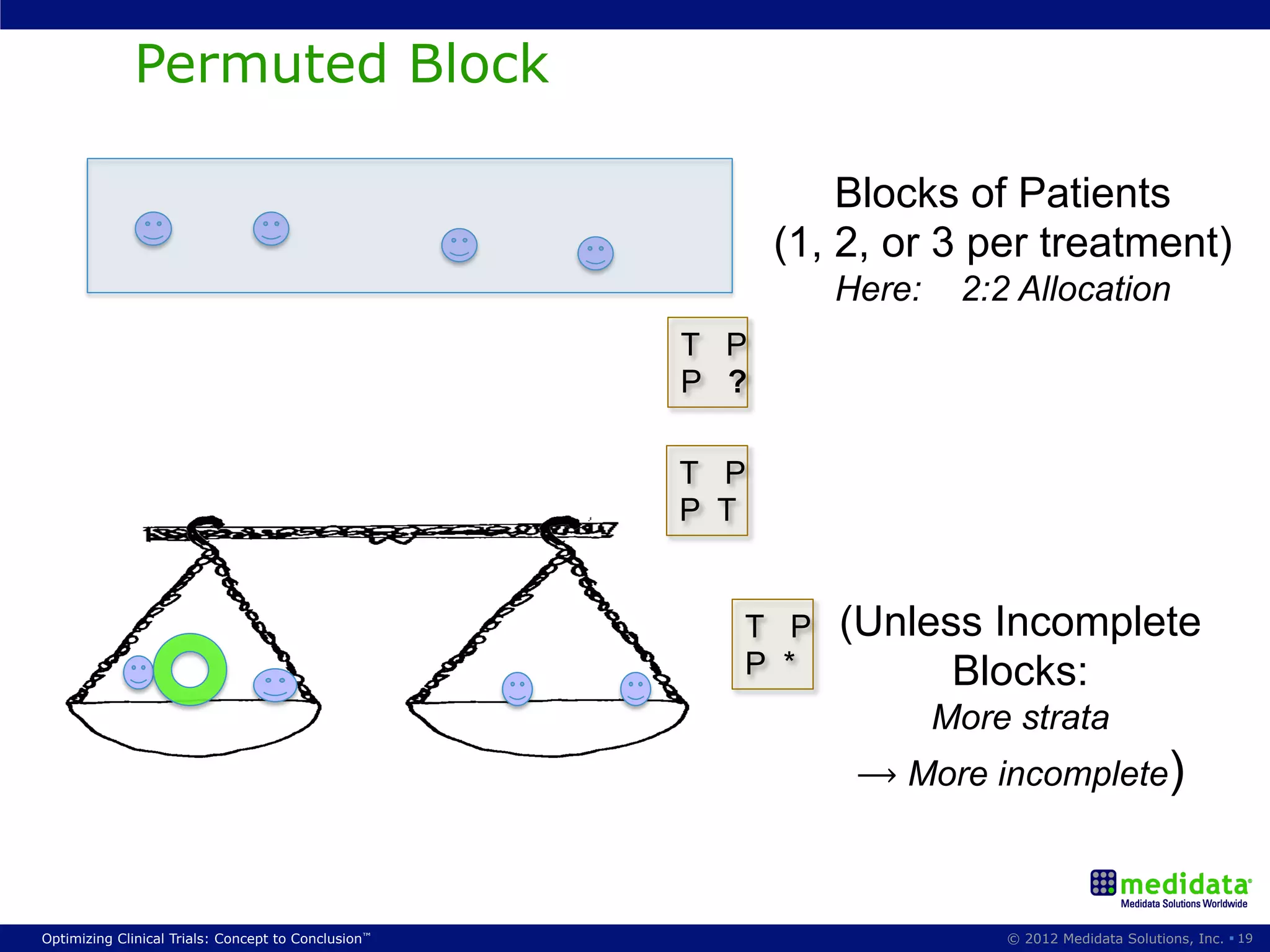
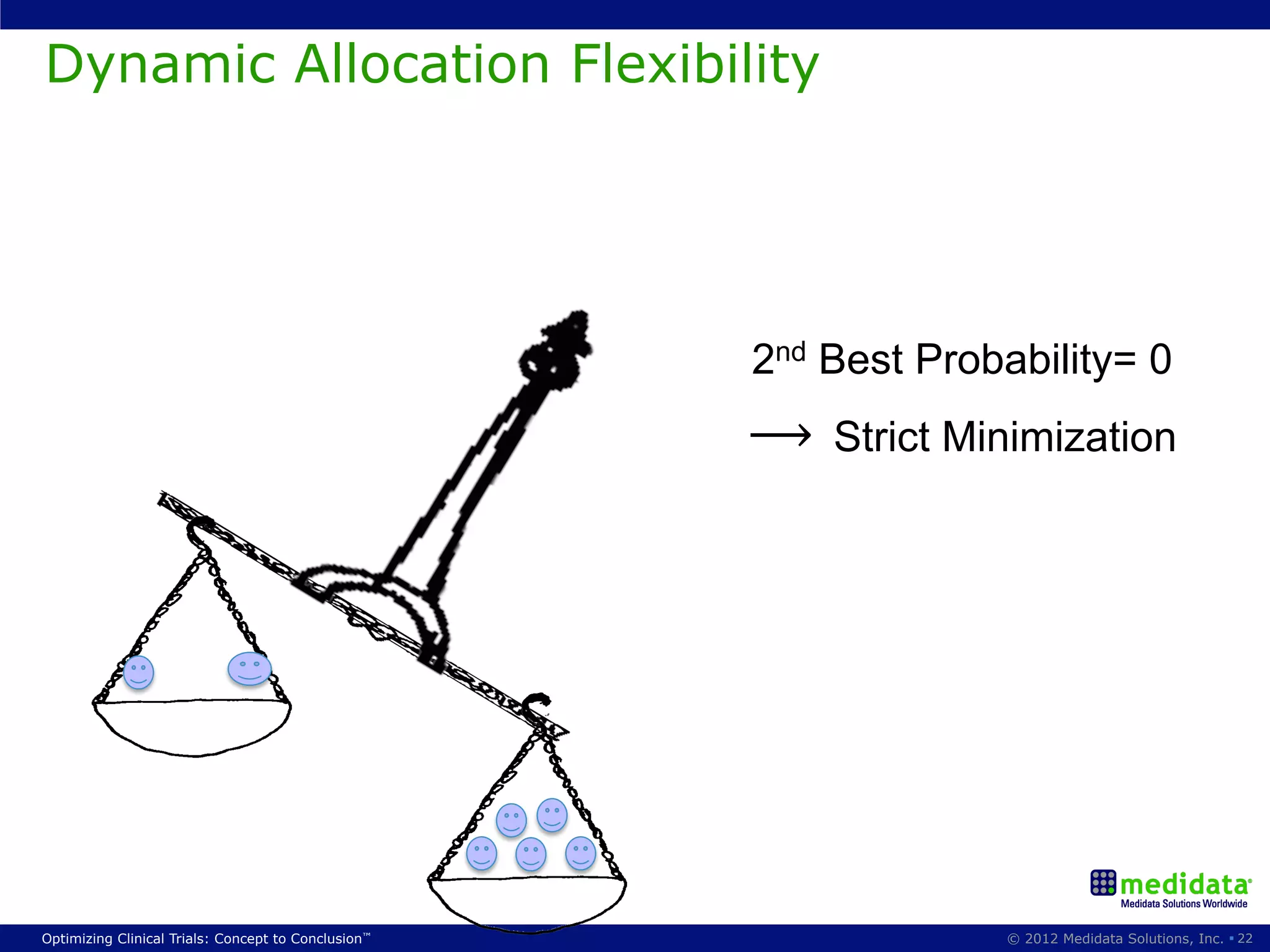
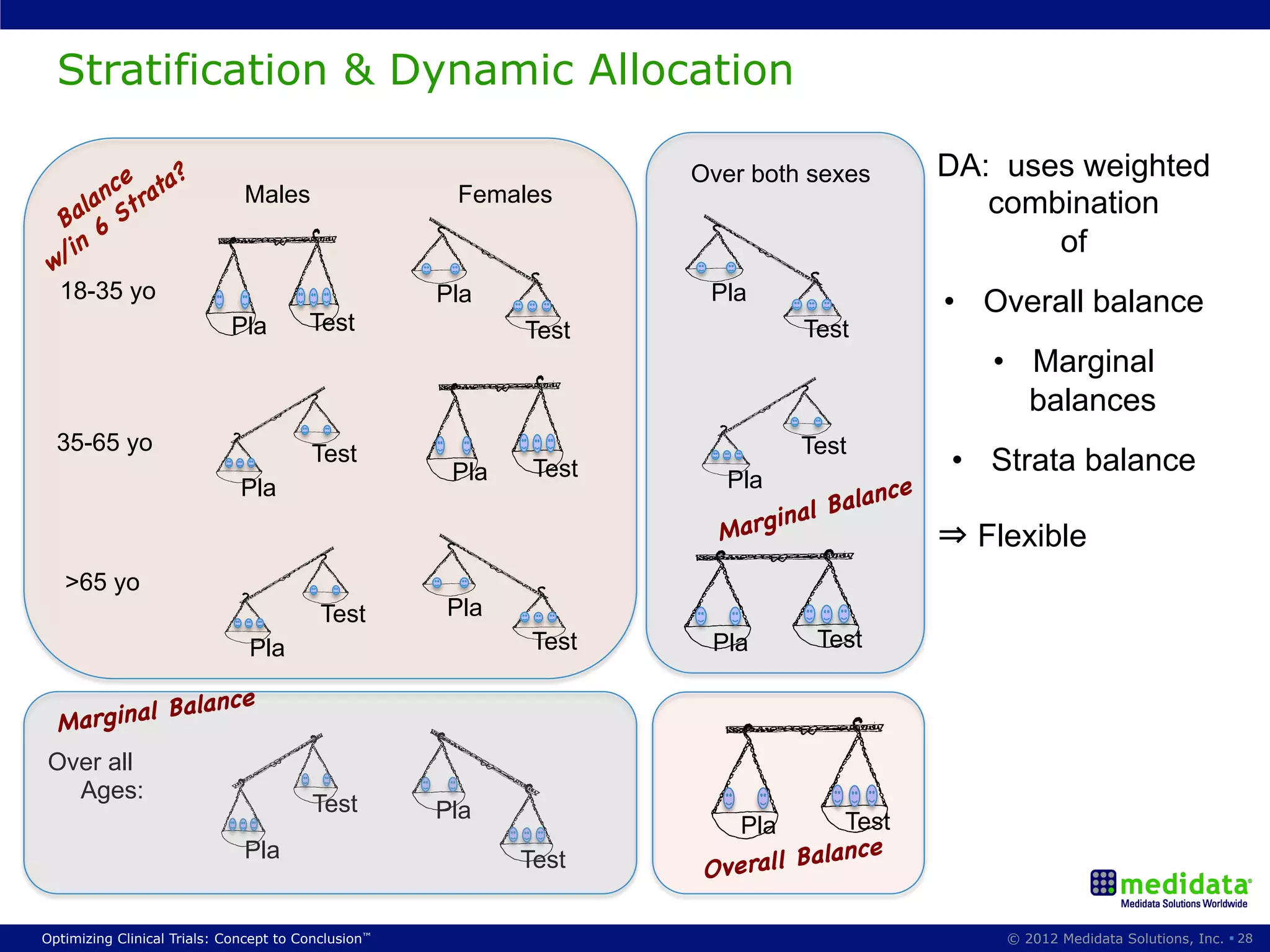
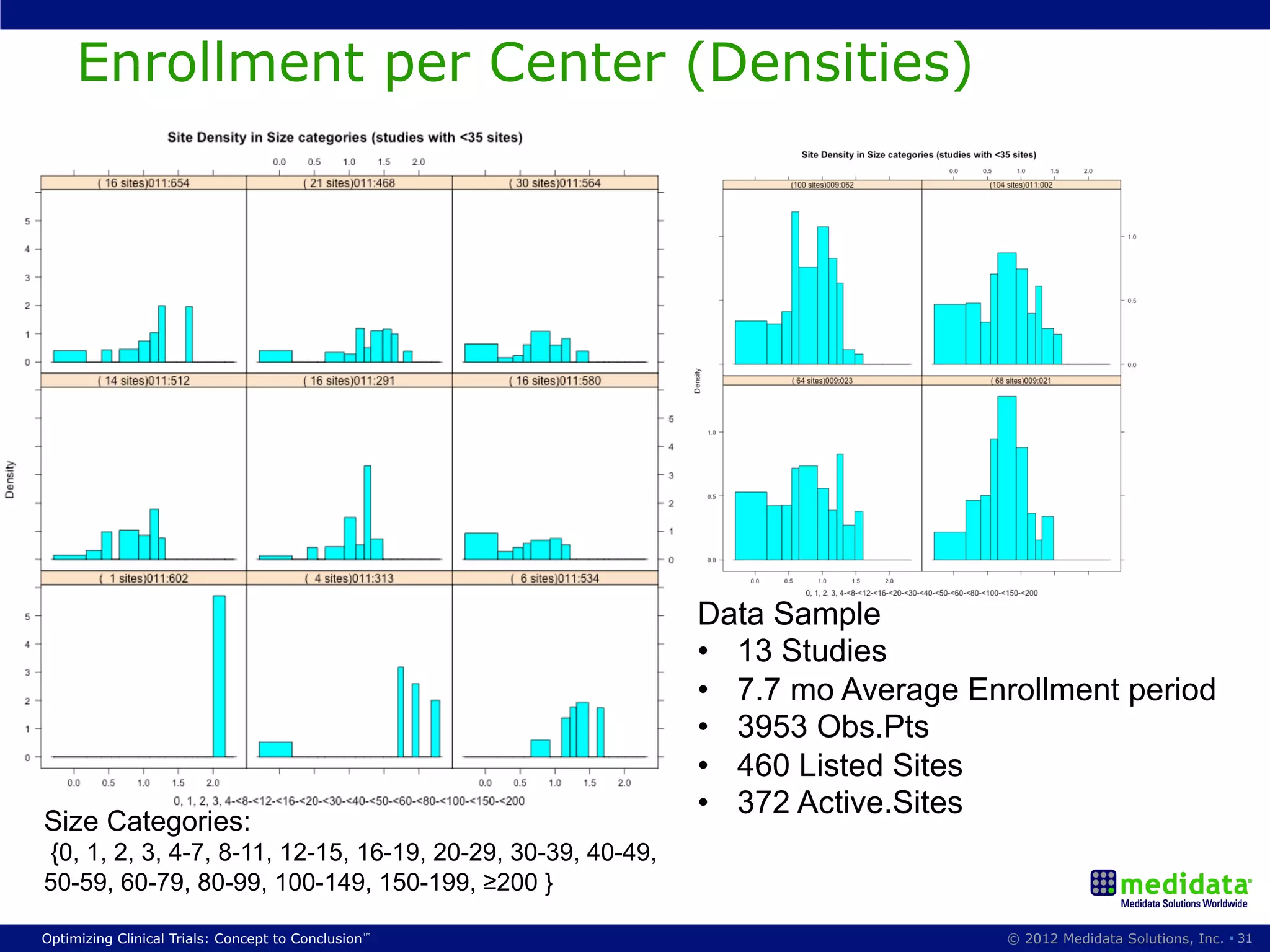
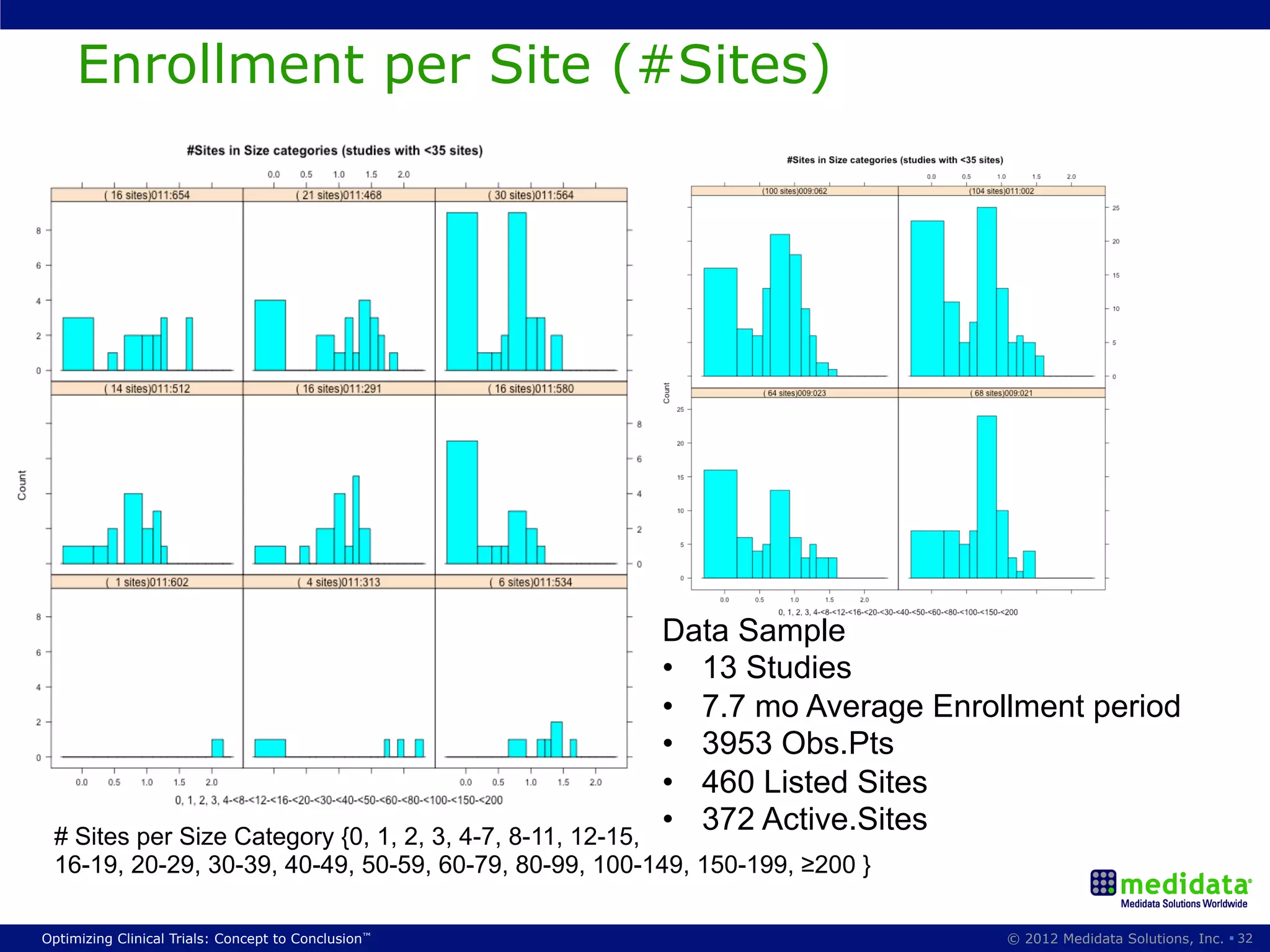
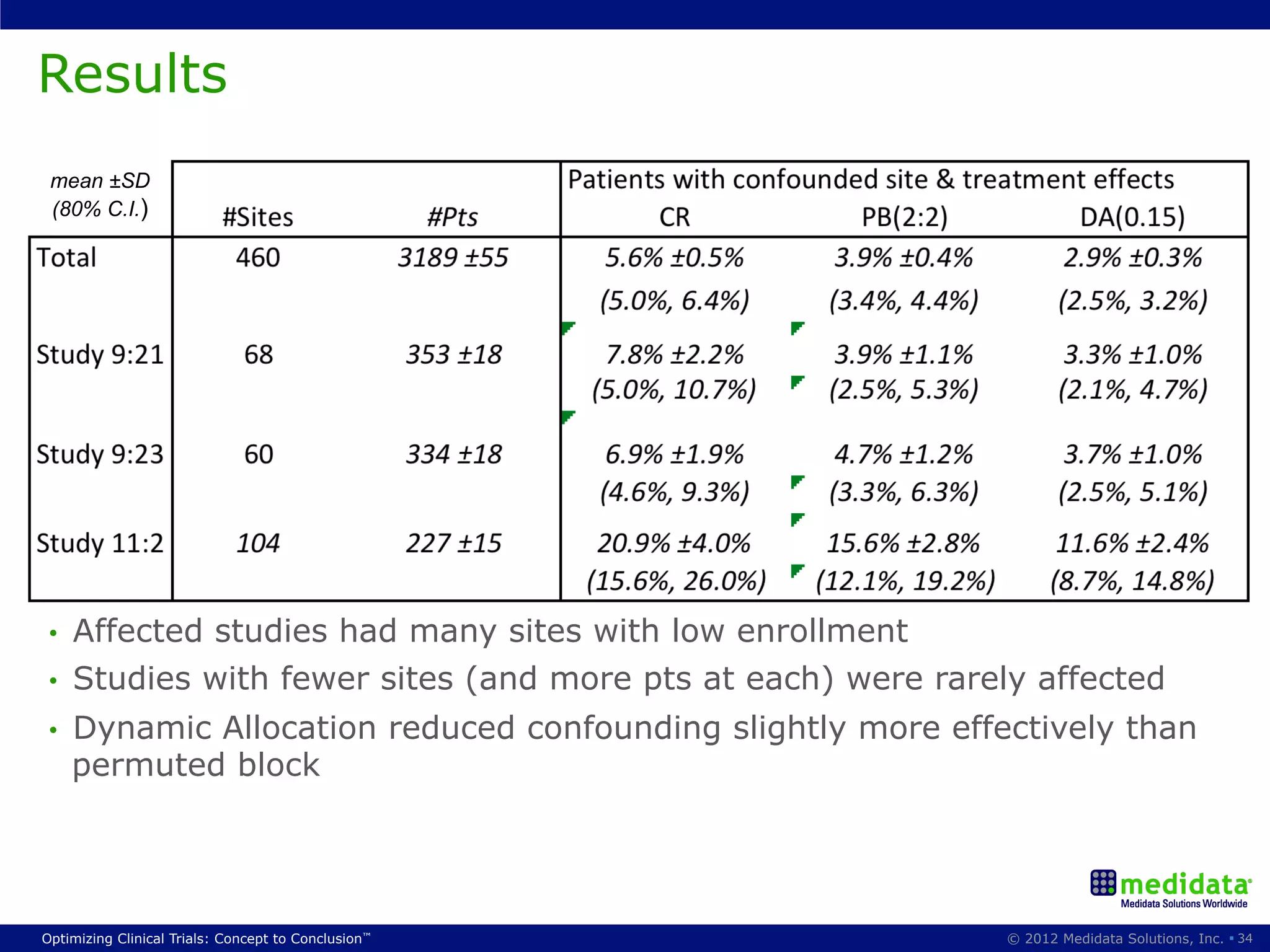
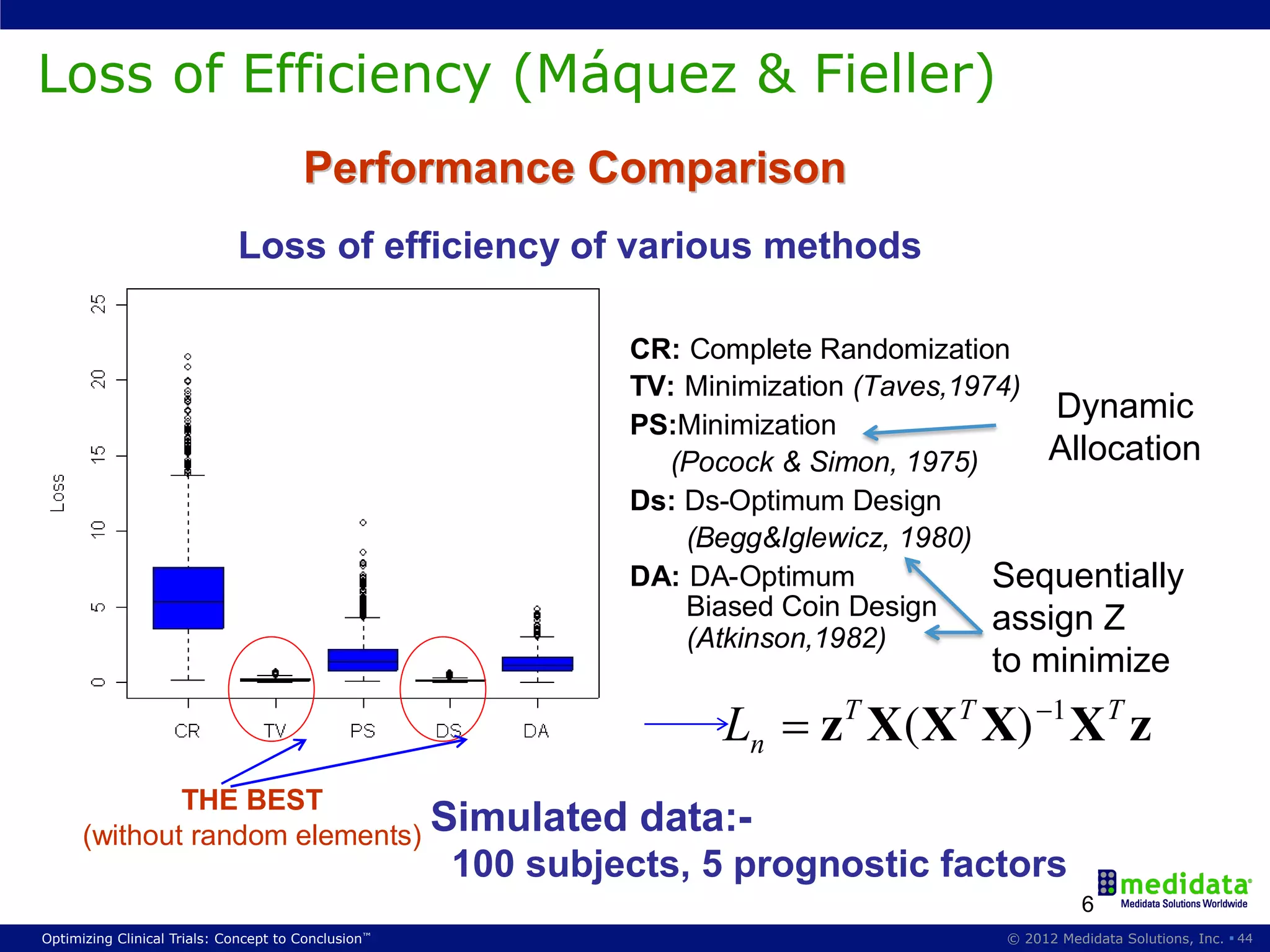
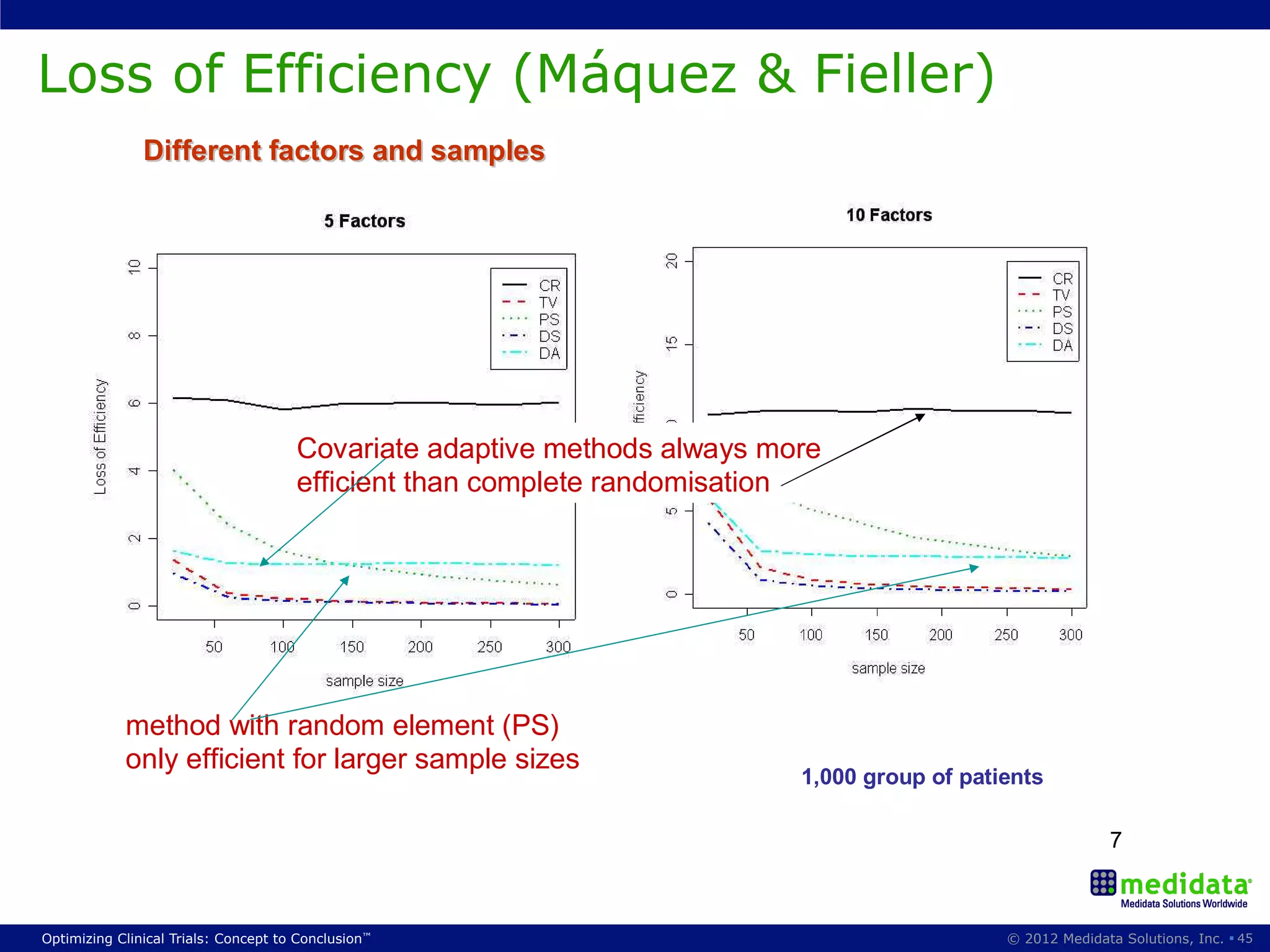
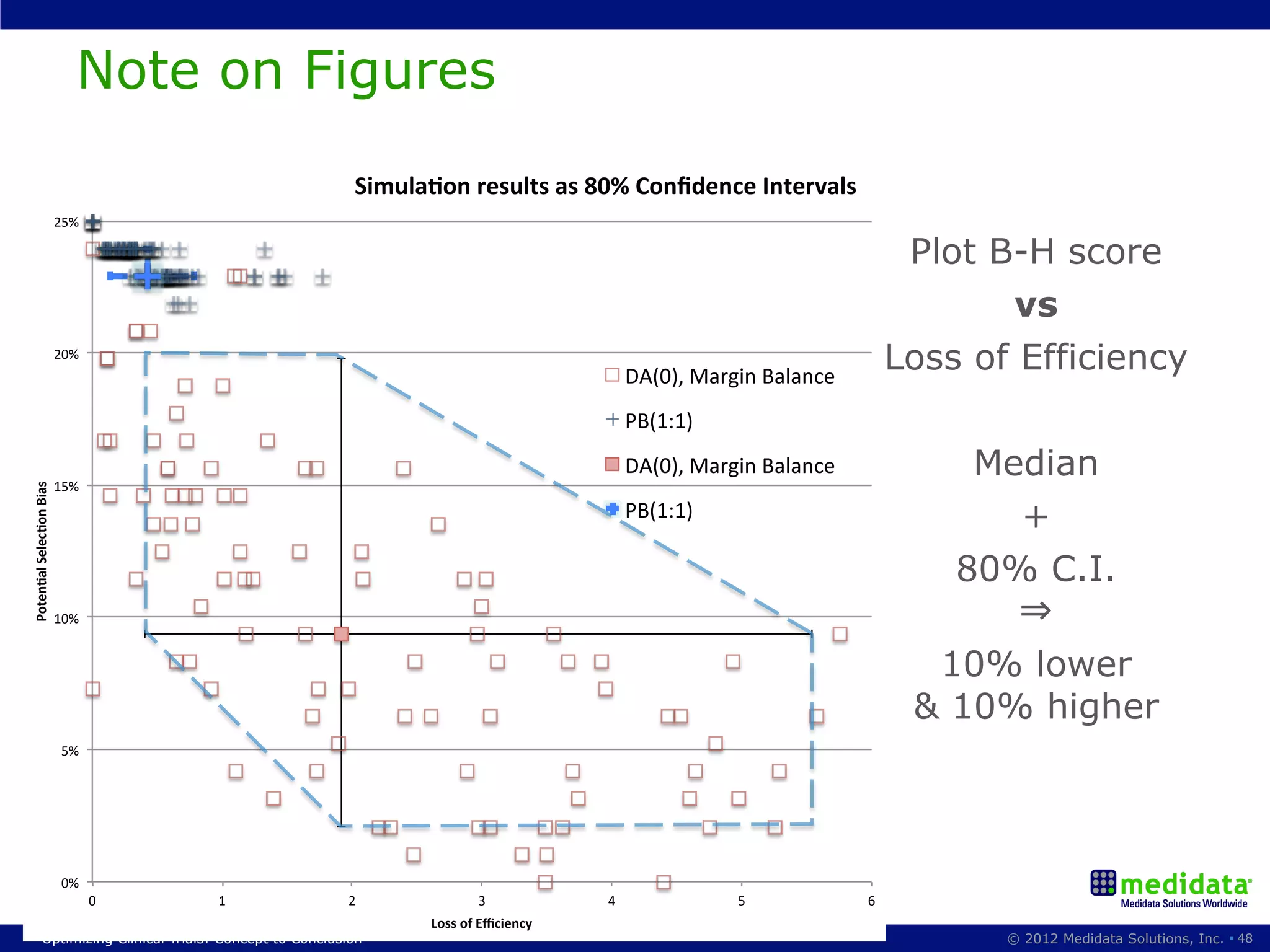
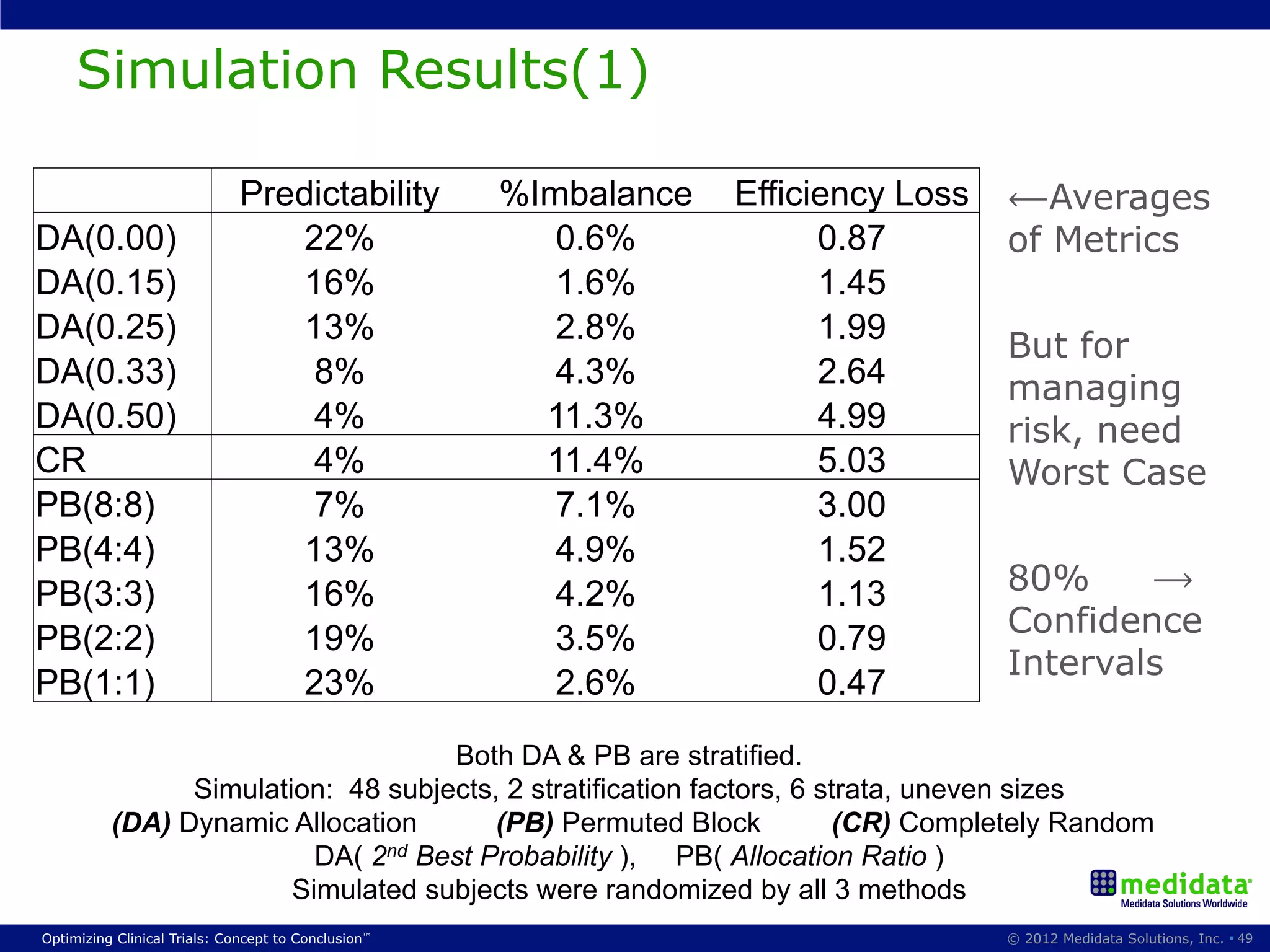
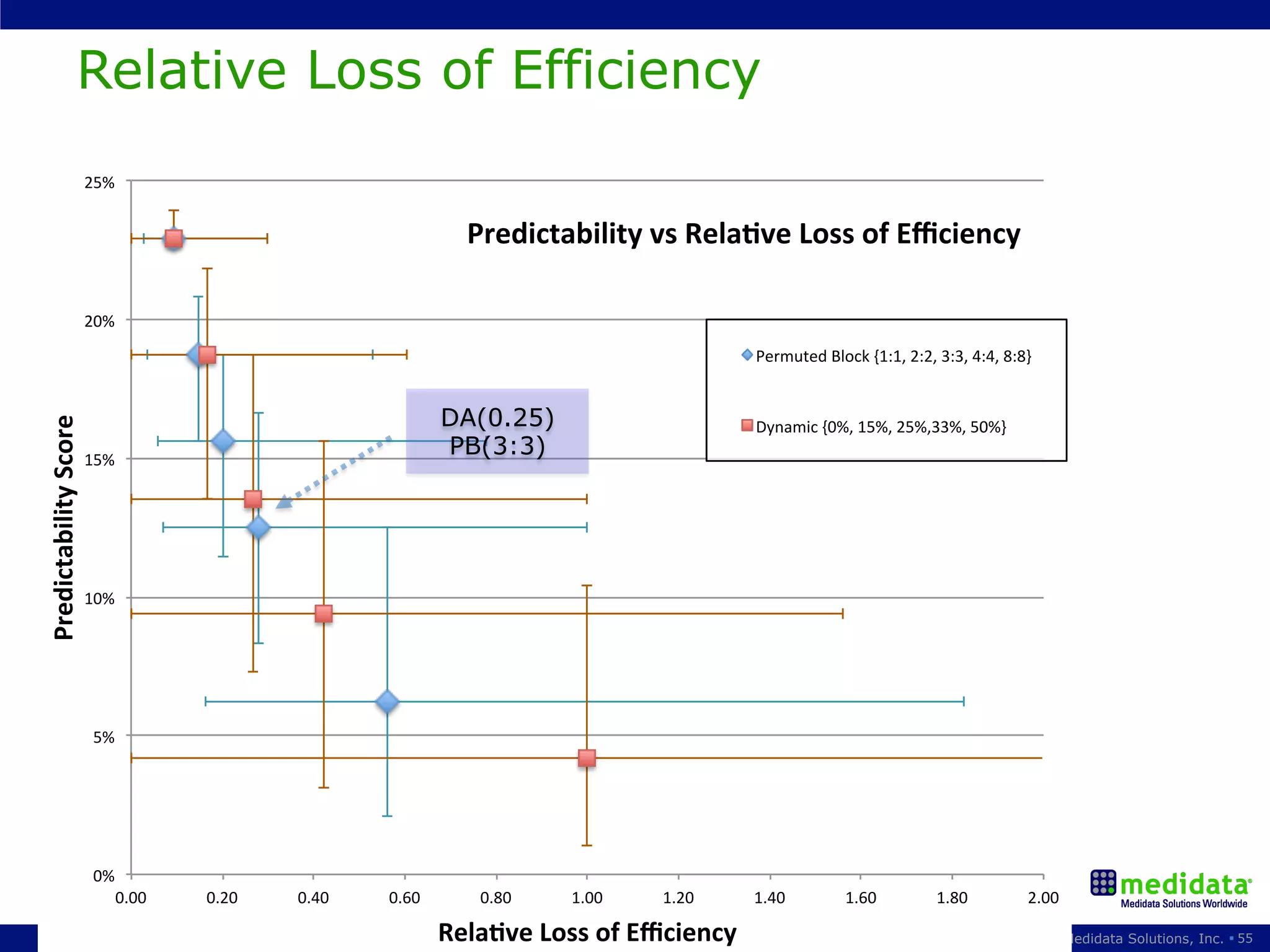
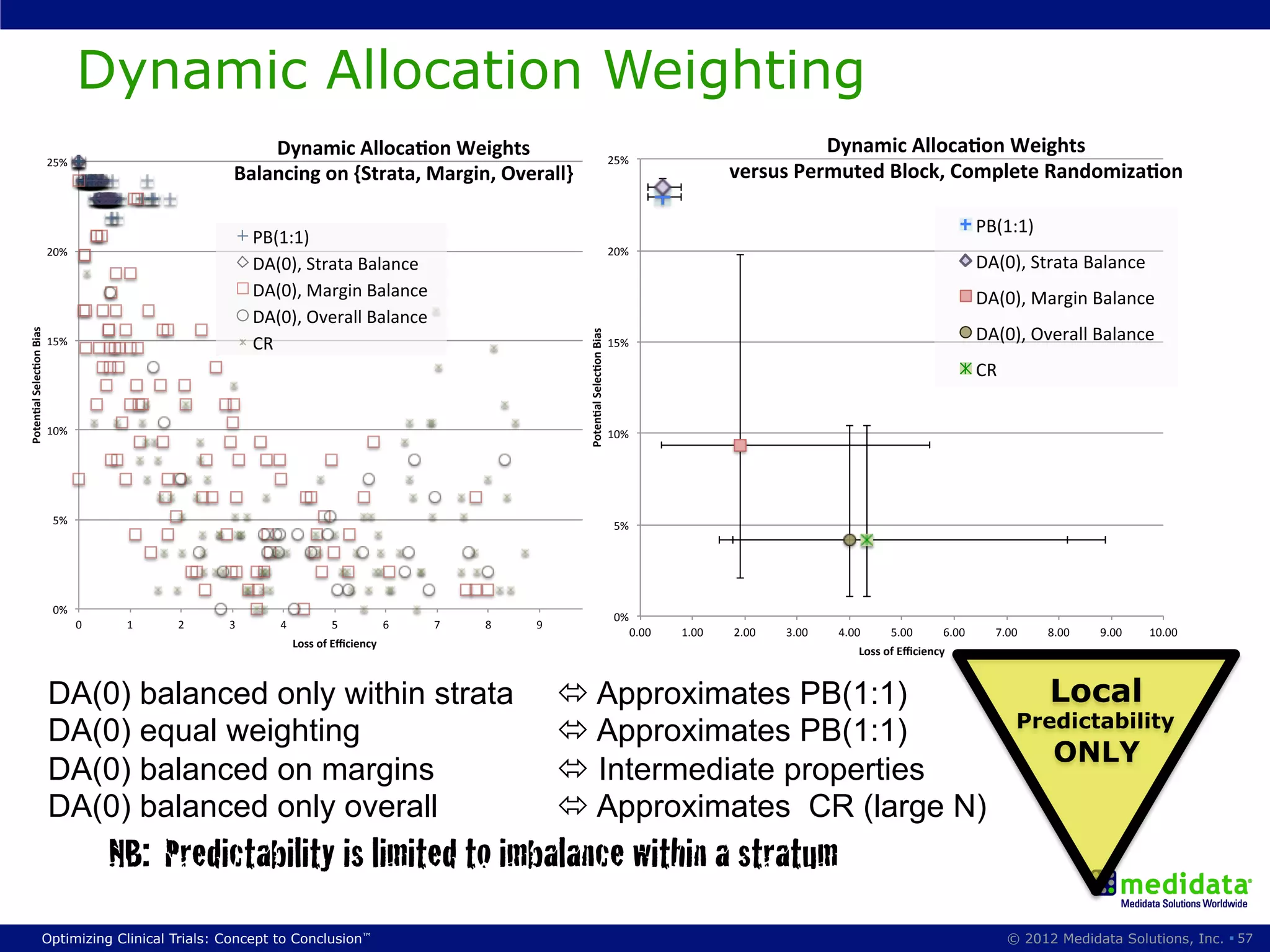
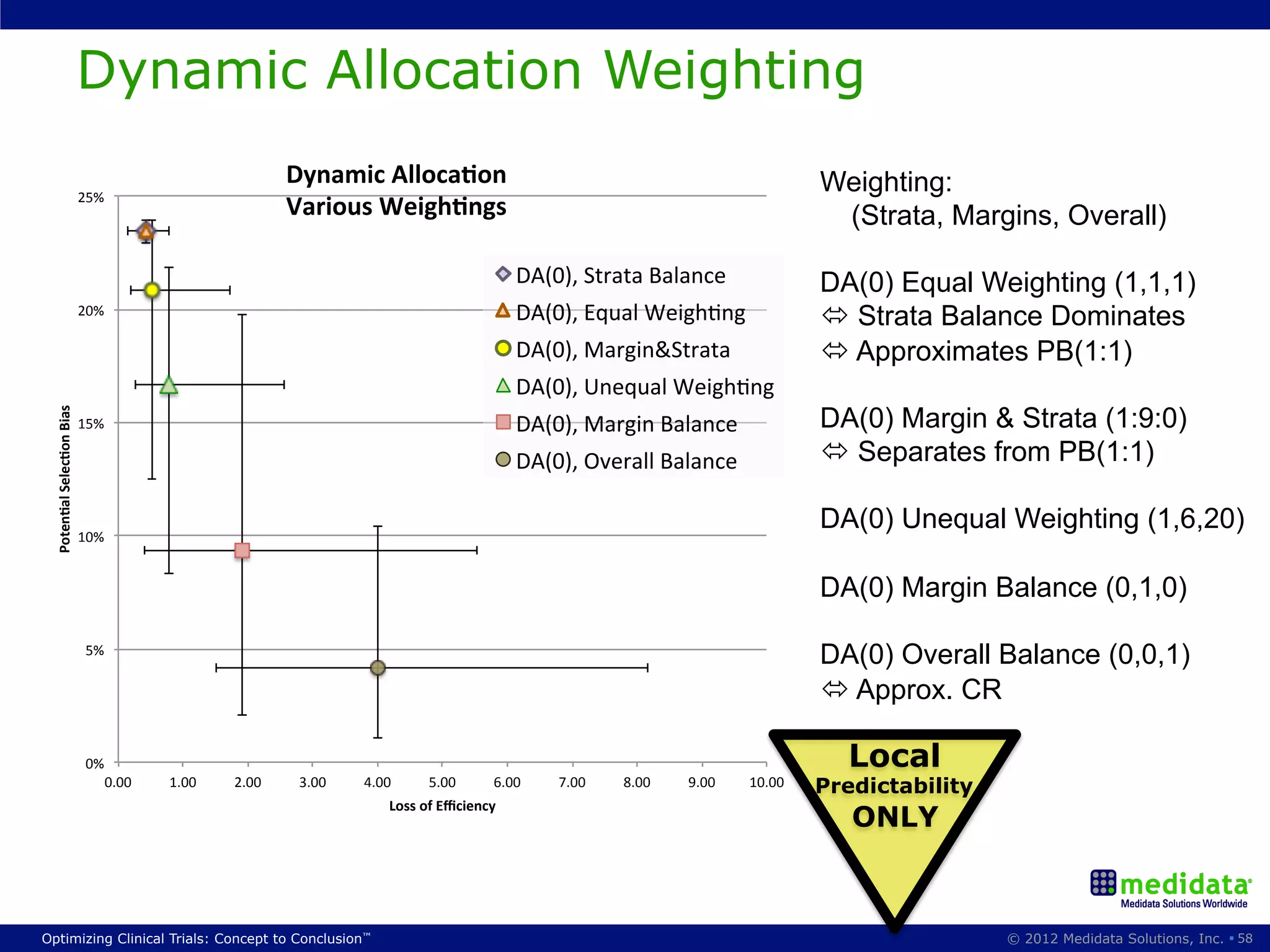
The document discusses randomization in clinical trials. It explains that randomization is important to minimize biases and balance treatment groups. Different randomization methods are presented: complete randomization, minimization, and permuted blocks. Metrics for evaluating randomization like balance, predictability, and loss of power are covered. Simulations comparing methods in terms of confounding factors, overall performance, and discontinuing patients are described. The importance of balanced treatment groups for sufficient statistical power and avoiding light weight results is emphasized.



































![addition way of usingstudy and factor imbalances. Furthermore, because of the importance of main-
A to the overall a random element to prevent determinism and avoid potential bias.
taining site balance and the fact that the International Conference on Harmonisation (ICH) guidelines
DA Algorithm
emphasizeswe introduce a new a multicenter trial should be stratified by study sites (ICH E9, 1998) is hig
Here, that randomization in generalized multidimensional dynamic allocation method that
[12], the method here specifically singlesrandomizationsite imbalance in the scoring formula.
flexible and can be applied to most out the overall scenarios.
In this generalized MDA method, when a new subject c needs to be assigned to a study arm Ai , we
calculate the weighted sum of the distance measure factor imbalances.
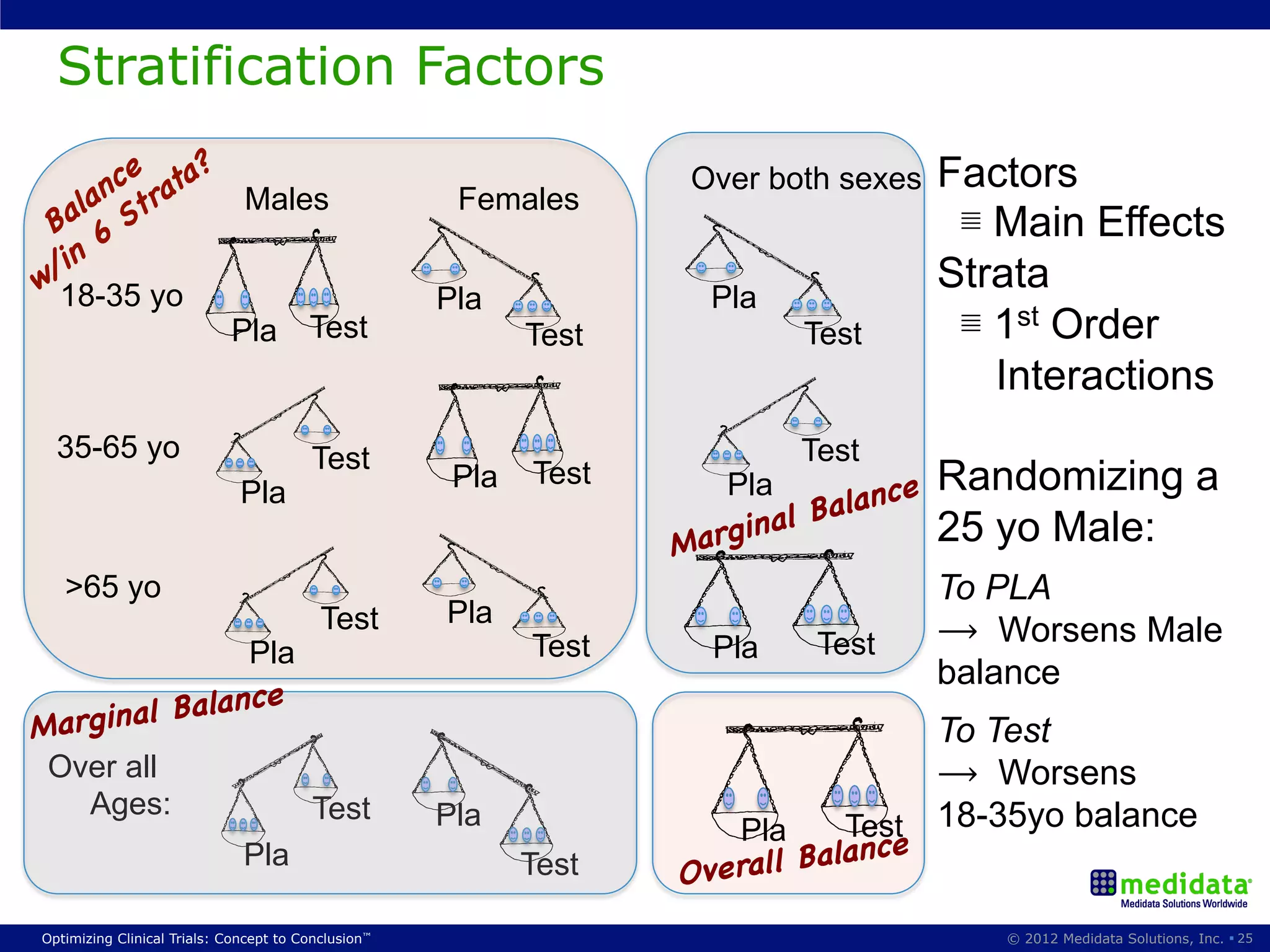
2.1. Marginal imbalance as study, site, strata and
Distance function ≣ Weighted Sum of Imbalances
IMB.c; Ai / D is a key rIMB.Study.c/; Ai // C .wSTRATUM rIMB.St ratum.c/; Ai //
Distance measure.wSTUDY component in DA methods. A number of distance measures have been p
posed, including range, standard deviation and variance [3, 7]. In this paper we use the marginal bala
C .wSITE rIMB.Site.c/; Ai //
X
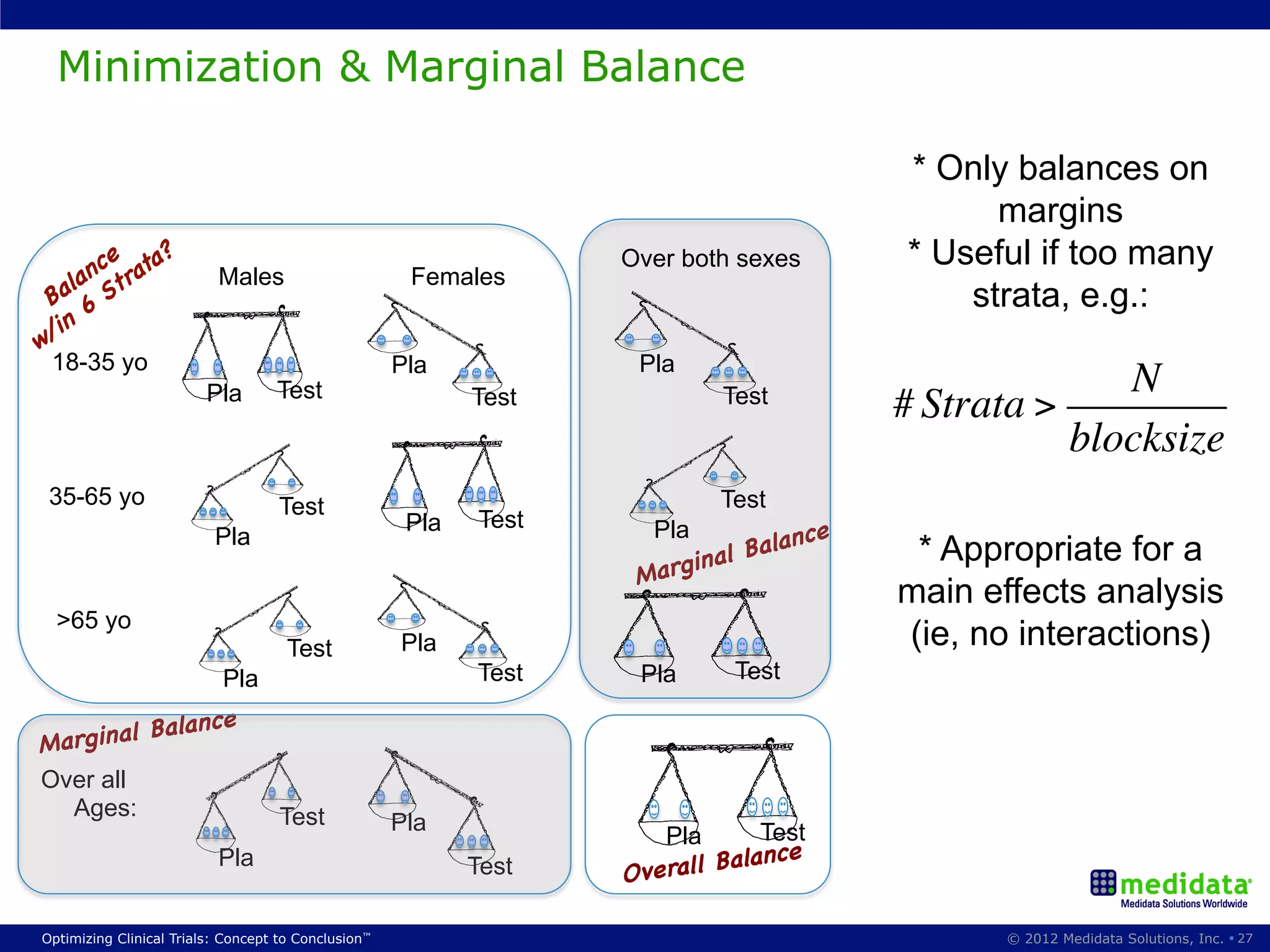
function as another measure of imbalance. For a actor.v; c/; Alevel, marginal balance has been descri
C .wFACTOR .v/ rIMB.F given factor i // (2)
as evaluating the overall balance of treatment allocation [10], and here the marginal imbalance func
16v6K
is defined as:
wSTUDY ; wSTRATUM ; Imbalance:
• Relative wSITE are the weights assigned to the study, stratum, and site imbalance respec-
ˇ ˇ
X ˇ ˇ X Av t h C ı.i; j /D 1; : : : ; K. Similarly
tively. Similarly, wFACTOR .v/ is the imbalance weight assigned the j factor, v ˇ
ˇ
S t udy.c/ is the set of all subjects randomized before c ˇinto the study, S i t e.c/ is rj ˇ set of subjects
rIMB.X; Ai / D the
ˇ .kX k C 1/ ˇ
randomized before c at c’s site, S t rat um.c/ is the subset of those that belong to the same site and share
16j 6N
the same factor levels as c across all factors, and F act or.v; c/ is the set of all the already randomized
where X share as Union of Strata already been randomized, kX k is the cardinality of
• Factor subset of the subjects c on the v factor.
subjects thatis any the same level or state as that haveth⇒
set X , N is the number of arms in the study, for i D 1; : : : ; N , Ai is the set of subjects already assig
P
2.3. arm Ai , ri assignment using the arm weight, (or ratio) for arm Ai1(so
to Treatment is the normalized generalized method , ri 1 1/, and ı.i; j / is
D
X= X ⇒ X ≥ X ⇒
As expected of a DAk method, arms that provide the least imbalance are collected into the
Kronecker delta.
first-choice set:X ∈X
k
X +1
≤
16i 6N
X +1
rIMB.X; Ai / provides a measure of the imbalance that would result from randomizing a new m
k k
ber of X into arm AiC.c/ Dmeasure is general, it does;:::;AN g IMB.c; Aj /gnumber of arms, and can han
F . This fAi W IMB.c; Ai / D minfA1 not depend on the (3)
⇒ and uneven arm ratios. This dominate Distance functionthe new class of multi-
both even Strata Imbalances feature makes it particularly useful for
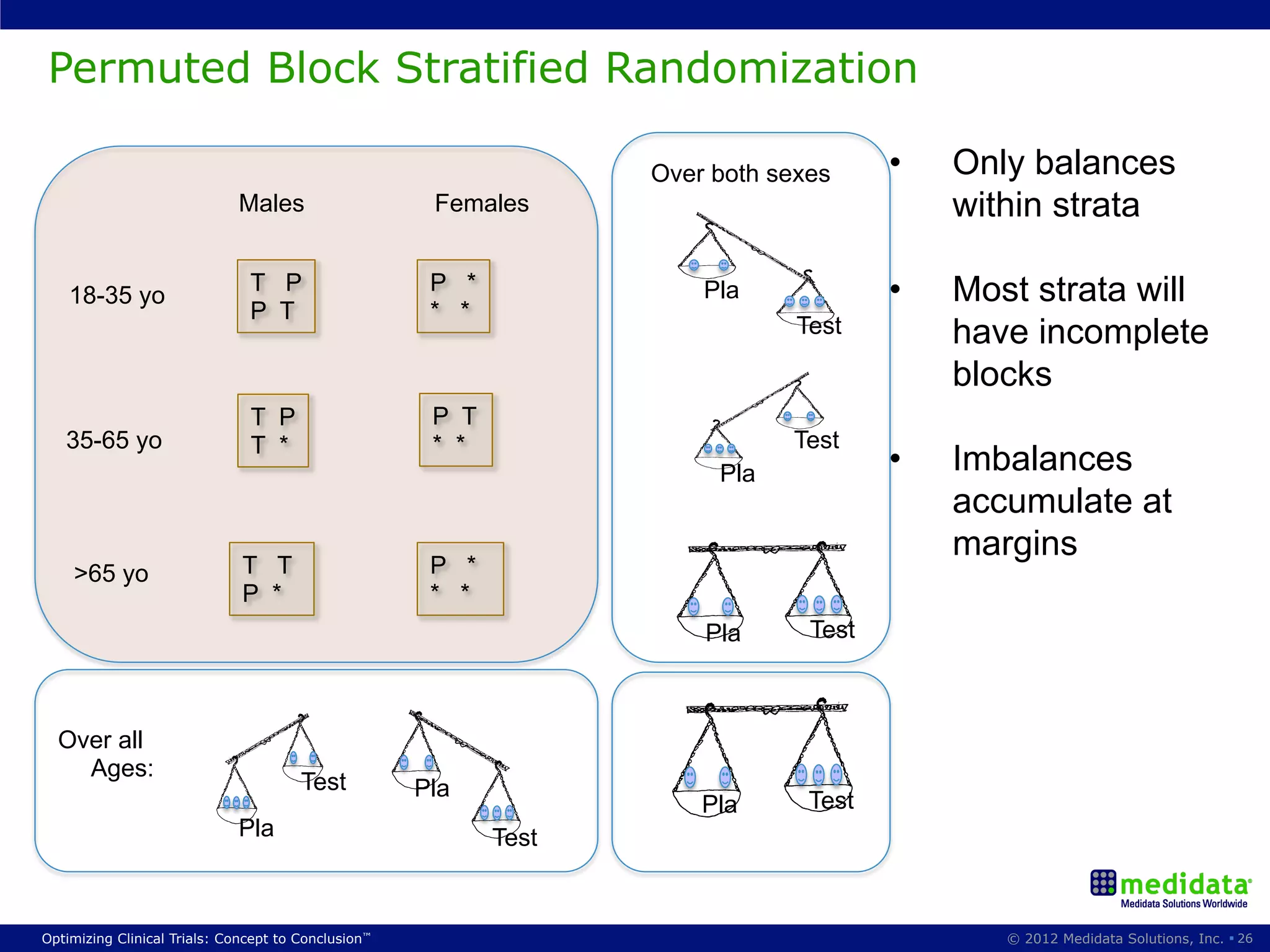
To keep the study balanced, it is also that unlike other distance measures, the any one of the arms
adaptive clinical trials. Note preferable that the subject c will be assigned to measure here is inversely p
in F C.c/. to the size of X . This ensures that an imbalance of n > 0 subjects on a small group will ‘cou
portional
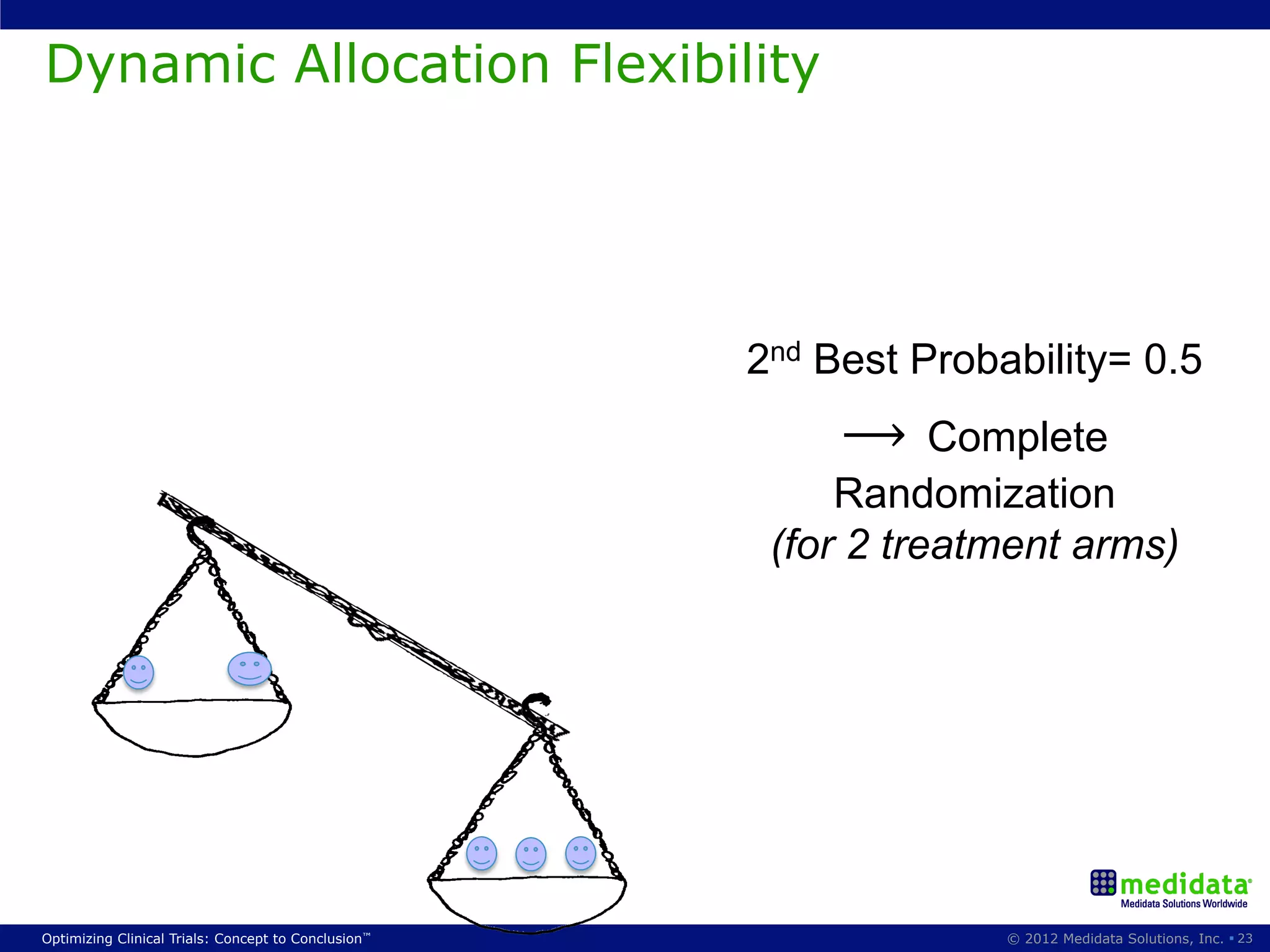
more than the method allows for the incorporation of a random element, a ‘Second Best Probability’
However,
an n subject imbalance on a larger group.
parameter that sets the Conclusion
Optimizing Clinical Trials: Concept to probability that even when there is just one best minimizing arm, 2012 Medidata Solutions, Inc. § 59
™ © that arm will](https://image.slidesharecdn.com/randomizationdeasa2012oct18-13533842508422-phpapp01-121119220619-phpapp01/75/Randomization-Too-Important-to-Gamble-with-59-2048.jpg)