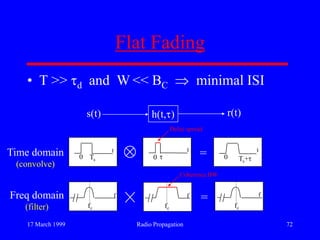
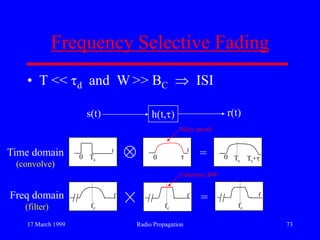
This document discusses radio propagation and propagation models. It begins with an introduction to radio and propagation mechanisms like free space propagation, refraction, diffraction, and scattering. It then discusses the objective of developing propagation models to predict signal strength at a receiver. The document outlines that propagation models are specialized based on scale, environment, and application. It covers large-scale path loss models and small-scale fading models. It discusses specific propagation mechanisms and models like free space, log-distance path loss, ground reflection, hilly terrain, indoor models, and statistical fading models.

1. Radio Propagation
CSCI 694
24 September 1999
Lewis Girod

2. 17 March 1999 Radio Propagation 2
Outline
• Introduction and terminology
• Propagation mechanisms
• Propagation models

3. 17 March 1999 Radio Propagation 3
What is Radio?
• Radio Xmitter induces E&M fields
– Electrostatic field components 1/d3
– Induction field components 1/d2
– Radiation field components 1/d
• Radiation field has E and B component
– Field strength at distance d = E B 1/d2
– Surface area of sphere centered at transmitter

4. 17 March 1999 Radio Propagation 4
General Intuition
• Two main factors affecting signal at receiver
– Distance (or delay) Path attenuation
– Multipath Phase differences
Green signal travels 1/2 farther than
Yellow to reach receiver, who sees Red.
For 2.4 GHz, (wavelength) =12.5cm.

5. 17 March 1999 Radio Propagation 5
Objective
• Invent models to predict what the field
looks like at the receiver.
– Attenuation, absorption, reflection, diffraction...
– Motion of receiver and environment…
– Natural and man-made radio interference...
– What does the field look like at the receiver?

6. 17 March 1999 Radio Propagation 6
Models are Specialized
• Different scales
– Large scale (averaged over meters)
– Small scale (order of wavelength)
• Different environmental characteristics
– Outdoor, indoor, land, sea, space, etc.
• Different application areas
– macrocell (2km), microcell(500m), picocell

7. 17 March 1999 Radio Propagation 7
Outline
• Introduction and some terminology
• Propagation Mechanisms
• Propagation models

8. 17 March 1999 Radio Propagation 8
Radio Propagation Mechanisms
• Free Space propagation
• Refraction
– Conductors & Dielectric materials (refraction)
• Diffraction
– Fresnel zones
• Scattering
– “Clutter” is small relative to wavelength

9. 17 March 1999 Radio Propagation 9
Free Space
• Assumes far-field (Fraunhofer region)
– d >> D and d >> , where
• D is the largest linear dimension of antenna
• is the carrier wavelength
• No interference, no obstructions

10. 17 March 1999 Radio Propagation 10
Free Space Propagation Model
• Received power at distance d is
– where Pt is the transmitter power in Watts
– a constant factor K depends on antenna gain, a
system loss factor, and the carrier wavelength
Watts)( 2
d
P
KdP t
r

11. 17 March 1999 Radio Propagation 11
Refraction
• Perfect conductors reflect
with no attenuation
• Dielectrics reflect a fraction
of incident energy
– “Grazing angles” reflect max*
– Steep angles transmit max*
r
t
• Reflection induces 180 phase shift
*The exact fraction depends on the materials and frequencies involved

12. 17 March 1999 Radio Propagation 12
Diffraction
• Diffraction occurs when waves
hit the edge of an obstacle
– “Secondary” waves propagated
into the shadowed region
– Excess path length results in
a phase shift
– Fresnel zones relate phase shifts
to the positions of obstacles
T
R
1st Fresnel zone
Obstruction

13. 17 March 1999 Radio Propagation 13
Fresnel Zones
• Bounded by elliptical loci of constant delay
• Alternate zones differ in phase by 180
– Line of sight (LOS) corresponds to 1st zone
– If LOS is partially blocked, 2nd zone can
destructively interfere (diffraction loss)
Fresnel zones are ellipses with the T&R at the foci; L1 = L2+
Path 1
Path 2

14. 17 March 1999 Radio Propagation 14
Power Propagated into Shadow
• How much power is propagated this way?
– 1st FZ: 5 to 25 dB below free space prop.
Obstruction of Fresnel Zones
1st 2nd
0
-10
-20
-30
-40
-50
-60
0o
90
180o
dB
Tip of Shadow
Obstruction
LOS
Rappaport, pp. 97

15. 17 March 1999 Radio Propagation 15
Scattering
• Rough surfaces
– critical height for bumps is f( ,incident angle)
– scattering loss factor modeled with Gaussian
distribution.
• Nearby metal objects (street signs, etc.)
– Usually modelled statistically
• Large distant objects
– Analytical model: Radar Cross Section (RCS)

16. 17 March 1999 Radio Propagation 16
Outline
• Introduction and some terminology
• Propagation Mechanisms
• Propagation models
– Large scale propagation models
– Small scale propagation (fading) models

17. 17 March 1999 Radio Propagation 17
Propagation Models: Large
• Large scale models predict behavior averaged
over distances >>
– Function of distance & significant environmental
features, roughly frequency independent
– Breaks down as distance decreases
– Useful for modeling the range of a radio system
and rough capacity planning

18. 17 March 1999 Radio Propagation 18
Propagation Models: Small
• Small scale (fading) models describe signal
variability on a scale of
– Multipath effects (phase cancellation)
dominate, path attenuation considered constant
– Frequency and bandwidth dependent
– Focus is on modeling “Fading”: rapid change in
signal over a short distance or length of time.

19. 17 March 1999 Radio Propagation 19
Large Scale Models
• Path loss models
• Outdoor models
• Indoor models

20. 17 March 1999 Radio Propagation 20
Free Space Path Loss
• Path Loss is a measure of attenuation based
only on the distance to the transmitter
• Free space model only valid in far-field;
– Path loss models typically define a “close-in”
point d0 and reference other points from there:
2
0
0
)()(
d
d
dPdP rr
dB
dBr
d
d
dPLdPdPL
0
0
2)()]([)(
What is dB?

21. 17 March 1999 Radio Propagation 21
Log-Distance Path Loss Model
• Log-distance generalizes path loss to
account for other environmental factors
• Choose a d0 in the far field.
• Measure PL(d0) or calculate Free Space Path Loss.
• Take measurements and derive empirically.
dB
d
d
dPLdPL
0
0
)()(

22. 17 March 1999 Radio Propagation 22
Log-Distance 2
• Value of characterizes different environments
Environm ent Exponent
Free Space 2
Urban area 2.7-3.5
Shadowed urban area 3-5
Indoor LOS 1.6-1.8
Indoor no LOS 4-6
Rappaport, Table 3.2, pp. 104

23. 17 March 1999 Radio Propagation 23
Log-Normal Shadowing Model
• Shadowing occurs when objects block LOS
between transmitter and receiver
• A simple statistical model can account for
unpredictable “shadowing”
– Add a 0-mean Gaussian RV to Log-Distance PL
– Markov model can be used for spatial correlation

24. 17 March 1999 Radio Propagation 24
Outdoor Models
• “2-Ray” Ground Reflection model
• Diffraction model for hilly terrain

25. 17 March 1999 Radio Propagation 25
2-Ray Ground Reflection
• For d >> hrht,
– low angle of incidence allows the earth to act
as a reflector
– the reflected signal is 180 out of phase
– Pr 1/d4 ( =4)
RT
ht hr
Phase shift!

26. 17 March 1999 Radio Propagation 26
Ground Reflection 2
• Intuition: ground blocks 1st Fresnel zone
– Reflection causes an instantaneous 180 phase shift
– Additional phase offset due to excess path length
– If the resulting phase is still close to 180 , the gound ray
will destructively interfere with the LOS ray.
RT
ht hr
p1
p0
180

27. 17 March 1999 Radio Propagation 27
Hilly Terrain
• Propagation can be LOS or result of
diffraction over one or more ridges
• LOS propagation modelled with
ground reflection: diffraction loss
• But if there is no LOS,
diffraction can actually help!

28. 17 March 1999 Radio Propagation 28
Indoor Path Loss Models
• Indoor models are less generalized
– Environment comparatively more dynamic
• Significant features are physically smaller
– Shorter distances are closer to near-field
– More clutter, scattering, less LOS

29. 17 March 1999 Radio Propagation 29
Indoor Modeling Techniques
• Modeling techniques and approaches:
– Log-Normal, <2 for LOS down corridor
– Log-Normal shadowing model if no LOS
– Partition and floor attenuation factors
– Computationally intensive “ray-tracing” based
on 3-D model of building and attenuation
factors for materials

30. 17 March 1999 Radio Propagation 30
Outline
• Introduction and some terminology
• Propagation Mechanisms
• Propagation models
– Large scale propagation models
– Small scale propagation (fading) models

31. 17 March 1999 Radio Propagation 31
Recall: Fading Models
• Small scale (fading) models describe signal
variability on a scale of
– Multipath effects (phase cancellation)
dominate, path attenuation considered constant
– Frequency and bandwidth dependent
– Focus is on modeling “Fading”: rapid change in
signal over a short distance or length of time.

32. 17 March 1999 Radio Propagation 32
Factors Influencing Fading
• Motion of the receiver: Doppler shift
• Transmission bandwidth of signal
– Compare to BW of channel
• Multipath propagation
– Receiver sees multiple instances of signal when
waves follow different paths
– Very sensitive to configuration of environment

33. 17 March 1999 Radio Propagation 33
Effects of Multipath Signals
• Rapid change in signal strength due to
phase cancellation
• Frequency modulation due to Doppler shifts
from movement of receiver/environment
• Echoes caused by multipath propagation
delay

34. 17 March 1999 Radio Propagation 34
The Multipath Channel
• One approach to small-scale models is to
model the “Multipath Channel”
– Linear time-varying function h(t, )
• Basic idea: define a filter that encapsulates
the effects of multipath interference
– Measure or calculate the channel impulse response
(response to a short pulse at fc):
h(t, )
t

35. 17 March 1999 Radio Propagation 35
Channel Sounding
• “Channel sounding” is a way to measure the
channel response
– transmit impulse, and measure the response to find h( ).
– h( ) can then be used to model the channel response to
an arbitrary signal: y(t) = x(t) h( ).
– Problem: models the channel at single point in time;
can‟t account for mobility or environmental changes
h(t, )
SKIP

36. 17 March 1999 Radio Propagation 36
Characterizing Fading*
• From the impulse response we can
characterize the channel:
• Characterizing distortion
– Delay spread ( d): how long does the channel
ring from an impulse?
– Coherence bandwidth (Bc): over what
frequency range is the channel gain flat?
– d 1/Bc
*Adapted from EE535 Slides, Chugg „99
In time domain, roughly corresponds to the “fidelity”
of the response; sharper pulse requires wider band

37. 17 March 1999 Radio Propagation 37
Effect of Delay Spread*
• Does the channel distort the signal?
– if W << Bc: “Flat Fading”
• Amplitude and phase distortion only
– if W > Bc: “Frequency Selective Fading”
• If T < d, inter-symbol interference (ISI) occurs
• For narrowband systems (W 1/T), FSF ISI.
• Not so for wideband systems (W >> 1/T)
For a system with bw W and symbol time T...

38. 17 March 1999 Radio Propagation 38
Qualitative Delay Spread
RMS Delay spread ( )
Mean excess delay
Noise threshold
Delay
Power(dB)
Typical values for :
Indoor: 10-100 ns
Outdoor: 0.1-10 s

39. 17 March 1999 Radio Propagation 39
Characterizing Fading 2*
• Characterizing Time-variation: How does
the impulse response change with time?
– Coherence time (tc): for what value of are
responses at t and t+ uncorrelated? (How
quickly is the channel changing)
– Doppler Spread (fd): How much will the
spectrum of the input be spread in frequency?
– fd 1/tc

40. 17 March 1999 Radio Propagation 40
Effect of Coherence Time*
• Is the channel constant over many uses?
– if T << tc: “Slow fading”
• Slow adaptation required
– if T > tc: “Fast fading”
• Frequent adaptation required
• For typical systems, symbol rate is high compared to
channel evolution
For a system with bw W and symbol time T...

41. 17 March 1999 Radio Propagation 41
Statistical Fading Models
• Fading models model the probability of a
fade occurring at a particular location
– Used to generate an impulse response
– In fixed receivers, channel is slowly time-varying; the
fading model is reevaluated at a rate related to motion
• Simplest models are based on the WSSUS
principle

42. 17 March 1999 Radio Propagation 42
WSSUS*
• Wide Sense Stationary (WSS)
– Statistics are independent of small perturbations in time
and position
– I.e. fixed statistical parameters for stationary nodes
• Uncorrelated Scatter (US)
– Separate paths are not correlated in phase or attenuation
– I.e. multipath components can be independent RVs
• Statistics modeled as Gaussian RVs

43. 17 March 1999 Radio Propagation 43
Common Distributions
• Rayleigh fading distribution
– Models a flat fading signal
– Used for individual multipath components
• Ricean fading distribution
– Used when there is a dominant signal
component, e.g. LOS + weaker multipaths
– parameter K (dB) defines strength of dominant
component; for K=- , equivalent to Rayleigh

44. 17 March 1999 Radio Propagation 44
Application of WSSUS
• Multi-ray Rayleigh fading:
– The Rayleigh distribution does not model
multipath time delay (frequency selective)
– Multi-ray model is the sum of two or more
independent time-delayed Rayleigh variables
s(t)
R1
R2
r(t)
Rappaport, Fig. 4.24, pp. 185.

45. 17 March 1999 Radio Propagation 45
Saleh & Valenzuela (1987)
• Measured same-floor indoor characteristics
– Found that, with a fixed receiver, indoor
channel is very slowly time-varying
– RMS delay spread: mean 25ns, max 50ns
– With no LOS, path loss varied over 60dB range
and obeyed log distance power law, 3 > n > 4
• Model assumes a structure and models
correlated multipath components.
Rappaport, pp. 188

46. 17 March 1999 Radio Propagation 46
Saleh & Valenzuela 2
• Multipath model
– Multipath components arrive in clusters, follow Poisson
distribution. Clusters relate to building structures.
– Within cluster, individual components also follow
Poisson distribution. Cluster components relate to
reflecting objects near the TX or RX.
– Amplitudes of components are independent Rayleigh
variables, decay exponentially with cluster delay and
with intra-cluster delay

47. 17 March 1999 Radio Propagation 47
References
• Wireless Communications: Principles and Practice, Chapters 3 and 4,
T. Rappaport, Prentice Hall, 1996.
• Principles of Mobile Communication, Chapter 2, G. Stüber, Kluwer
Academic Publishers, 1996.
• Slides for EE535, K. Chugg, 1999.
• Spread Spectrum Systems, Chapter 7, R. Dixon, Wiley, 1985 (there is a
newer edition).
• Wideband CDMA for Third Generation Mobile Communications,
Chapter 4, T. Ojanpera, R. Prasad, Artech, House 1998.
• Propagation Measurements and Models for Wireless Communications
Channels, Andersen, Rappaport, Yoshida, IEEE Communications,
January 1995.

48. 17 March 1999 Radio Propagation 48
The End

49. 17 March 1999 Radio Propagation 49
Scattering 2
• hc is the critical height of a protrusion to
result in scattering.
• RCS: ratio of power density scattered to receiver
to power density incident on the scattering object
– Wave radiated through free space to scatterer and reradiated:
)sin( θ8
λ
i
c
h
)log(20)log(20)π4log(30
]dB[)λlog(20)dBi()dBm()dBm(
2
RT
TTR
dd
mRCSGPP

50. 17 March 1999 Radio Propagation 50
Free Space 2a
• Free space power flux density (W/m2)
– power radiated over surface area of sphere
– where Gt is transmitter antenna gain
• By covering some of this area, receiver‟s
antenna “catches” some of this flux
2
π4 d
GP
P tt
d

51. 17 March 1999 Radio Propagation 51
Free Space 2b
• Fraunhofer distance: d > 2D2/
• Antenna gain and antenna aperture
– Ae is the antenna aperture, intuitively the area
of the antenna perpendicular to the flux
– Gr is the antenna gain for a receiver. It is related to Ae.
– Received power (Pr) = Power flux density (Pd) * Ae
2
λ
π4 e
A
G
π4
λ
2
G
Ae

52. 17 March 1999 Radio Propagation 52
Free Space 2c
– where L is a system loss factor
– Pt is the transmitter power
– Gt and Gr are antenna gains
– is the carrier wavelength
Watts
)π(4
λ1
)( 2
2
2
L
GGP
d
dP rtt
r

53. 17 March 1999 Radio Propagation 53
LNSM 2
• PL(d)[dB] = PL(d0) +10nlog(d/d0)+ X
– where X is a zero-mean Gaussian RV (dB)
• and n computed from measured data,
based on linear regression

54. 17 March 1999 Radio Propagation 54
Ground Reflection 1.5
• The power at the receiver in this model is
– derivation calculates E field;
– Pr = |E|2Ae; Ae is ant. aperture
• The “breakpoint” at which the model
changes from 1/d2 to 1/d4 is 2 hthr/
– where hr and ht are the receiver and transmitter
antenna heights
4
22
d
hh
GGPP rt
rttr

55. 17 March 1999 Radio Propagation 55
Convolution Integral
• Convolution is defined by this integral:
τ)τ()τ()(
)()()(
dthxty
thtxty
Indexes relevant portion
of impulse response
Scales past input signal

56. 17 March 1999 Radio Propagation 56
Partition Losses
• Partition losses: same floor
– Walls, furniture, equipment
– Highly dependent on type of material, frequency
• Hard partitions vs soft partitions
– hard partitions are structural
– soft partitions do not reach ceiling
• “open plan” buildings

57. 17 March 1999 Radio Propagation 57
Partition Losses 2
• Partition losses: between floors
– Depends on building construction, frequency
– “Floor attenuation factor” diminishes with
successive floors
– typical values:
• 15 dB for 1st floor
• 6-10 dB per floor for floors 2-5
• 1-2 dB per floor beyond 5 floors

58. 17 March 1999 Radio Propagation 58
Materials
• Attenuation values for different materials
M aterial Loss (dB) Frequency
Concrete block 13-20 1.3 GHz
Plywood (3/4”) 2 9.6 GHz
Plywood (2 sheets) 4 9.6 GHz
Plywood (2 sheets) 6 28.8 GHz
Alum inum siding 20.4 815 M Hz
Sheetrock (3/4”) 2 9.6 GHz
Sheetrock (3/4”) 5 57.6 GHz
Turn corner in corridor 10-15 1.3 GHz

59. 17 March 1999 Radio Propagation 59
What does “dB” mean?
• dB stands for deciBel or 1/10 of a Bel
• The Bel is a dimensionless unit for
expressing ratios and gains on a log scale
• Gains add rather than multiply
• Easier to handle large dynamic ranges
))log()(log(10log10
P
P
12
1
2
10
dB1
2
PP
P
P

60. 17 March 1999 Radio Propagation 60
dB 2
• Ex: Attenuation from transmitter to receiver.
– PT=100, PR=10
– attenuation is ratio of PT to PR
– [PT/PR]dB = 10 log(PT/PR) = 10 log(10) = 10 dB
• Useful numbers:
– [1/2]dB -3 dB
– [1/1000]dB = -30 dB

61. 17 March 1999 Radio Propagation 61
dB 3
• dB can express ratios, but what about
absolute quantities?
• Similar units reference an absolute quantity
against a defined reference.
– [n mW]dBm = [n/mW]dB
– [n W]dBW = [n/W]dB
• Ex: [1 mW]dBW = -30 dBW

62. 17 March 1999 Radio Propagation 62
Channel Sounding 2
• Several “Channel Sounding” techniques can
measure the channel response directly:
– Direct RF pulse (we hinted at this approach)
– Sliding correlator
– Frequency domain sounding

63. 17 March 1999 Radio Propagation 63
Channel Sounding 3
• Direct RF Pulse
– Xmit pulse, scope displays response at receiver
– Can be done with off-the-shelf hardware
– Problems: hard to reject noise in the channel
– If no LOS
• must trigger scope on weaker multipath component
• may fail to trigger
• lose delay and phase information

64. 17 March 1999 Radio Propagation 64
Channel Sounding 4
• Sliding correlator
– Xmit PseudoNoise sequence
– Rcvr correlates signal with its PN generator
– Rcvr clock slightly slower; PN sequences slide
– Delayed components cause delayed correlations
– Good resolution, good noise rejection

65. 17 March 1999 Radio Propagation 65
Channel Sounding 5
• Frequency domain sounding
– Sweep frequency range
– Compute inverse Fourier transform of response
– Problems
• not instantaneous measurement
• Tradeoff between resolution (number of frequency
steps) and real-time measurement (i.e. duration as
short as possible)

66. 17 March 1999 Radio Propagation 66
Digression: Convolutions
• The impulse response “box” notation
implies the convolution operator,
– Convolution operates on a signal and an
impulse response to produce a new signal.
– The new signal is the superposition of the
response to past values of the signal.
– Commutative, associative

67. 17 March 1999 Radio Propagation 67
y(t)
y(t)
Convolutions 2
• y(t) is the sum of scaled, time-delayed responses
x(t) h(t) =
+
h(t)
Each component of the sum is scaled
by the x(t)dt at that point; in this
example, the response is scaled to 0
where x(t) = 0.

68. 17 March 1999 Radio Propagation 68
Flip & Slide: h(t- )h(t- ) Flip & Slide: h(t- )h(t- ) Flip & Slide: h(t- )h(t- )
Convolutions 3
• Graphical method: “Flip & Slide”
x(t)
x( )
h(t) =
Pairwise multiply x*h
and integrate over
and Store y(t)
y(t)
y(t)
Flip & Slide: h(t- )h(t- ) Flip & Slide: h(t- )h(t- )

69. 17 March 1999 Radio Propagation 69
Frequency and Time Domains
• The channel impulse response is f(time)
– It describes the channel in the “time domain”
• Functions of frequency are often very useful;
– Space of such functions is “frequency domain”
• Often a particular characteristic is easier to
handle in one domain or the other.

70. 17 March 1999 Radio Propagation 70
Frequency Domain
• Functions of frequency
– usually capitalized and take the parameter “f”
– where f is the frequency in radians/sec
– and the value of the function is the amplitude of
the component of frequency f.
• Convolution in time domain translates into
multiplication in the frequency domain:
– y(t) = x(t) h(t) Y(f) = X(f)H(f)

71. 17 March 1999 Radio Propagation 71
Frequency Domain 2
• Based on Fourier theorem:
– any periodic signal can be decomposed into a
sum of (possibly infinite number of) cosines
• The Fourier Transform and inverse FT
– Convert between time and frequency domains.
– The frequency and time representations of the
same signal are “duals”

72. 17 March 1999 Radio Propagation 72
Flat Fading
• T >> d and W << BC minimal ISI
0 Ts 0 0 Ts+
fc fcfc
t t t
f f f
s(t) r(t)h(t, )
Time domain
(convolve)
Freq domain
(filter)
=
=
Delay spread
Coherence BW

73. 17 March 1999 Radio Propagation 73
Frequency Selective Fading
• T << d and W >> BC ISI
0 Ts 0 0 Ts+
fc fcfc
t t
f f f
s(t) r(t)h(t, )
Time domain
(convolve)
Freq domain
(filter)
=
=
Delay spread
Coherence BW
Ts

74. 17 March 1999 Radio Propagation 74
Review
• Object of radio propagation models:
– predict signal quality at receiver
• Radio propagation mechanisms
– Free space (1/d2)
– Diffraction
– Refraction
– Scattering

75. 17 March 1999 Radio Propagation 75
Review 2
• Factors influencing received signal
– Path loss: distance, obstructions
– Multipath interference: phase cancellation due
to excess path length and other sources of phase
distortion
– Doppler shift
– Other radio interference

76. 17 March 1999 Radio Propagation 76
Review 3
• Approaches to Modelling
– Models valid for far-field, apply to a range of
distances
– large scale models: concerned with gross
behavior as a function of distance
– small scale (fading) models: concerned with
behavior during perturbations around a
particular distance

77. 17 March 1999 Radio Propagation 77
Relevance to Micronets
• Micronets may require different models
than most of the work featured here
– Smaller transmit range
– Likely to be near reflectors: on desk or floor.
• On the other hand, at smaller scales things are less
smooth: “ground reflection” may turn into scattering
– Outdoors, throwing sensors on ground may not
work. Deployable tripods?

78. 17 March 1999 Radio Propagation 78
Relevance 2
• Consequences of “Fading”
– You can be in a place that has no signal, but
where a signal can be picked up a short distance
away in any direction
• Ability to move? Switch frequencies/antennas? Call
for help moving or for more nodes to be added?
• If stuck, may not be worth transmitting at all
– Reachability topology may be completely
irrelevant to location relationships

79. 17 March 1999 Radio Propagation 79
Relevance 3
• Relevant modelling tools:
– Statistical models (Rice/Rayleigh/Log Normal)
• Statistical fading assumes particular dynamics, this
depends on mobility of receivers and environment
– CAD modelling of physical environment and
ray tracing approaches.
• For nodes in fixed positions this is only done once.

80. 17 March 1999 Radio Propagation 80
Relevance 4
• An approach to modelling?
– Characterize wireless system interactions with
different materials, compare to published data
– Assess the effect of mobility in environment on fixed
topologies, relate to statistical models
– Try to determine what environmental structures and
parameters are most important:
• Scattering vs. ground reflection?
• can a simple CAD model help?