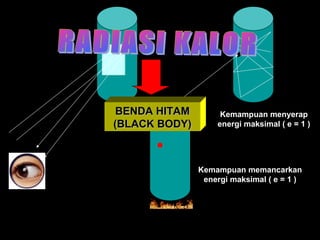
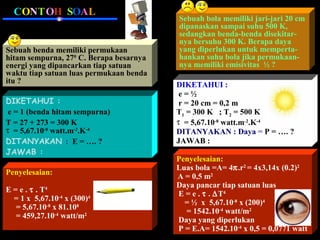
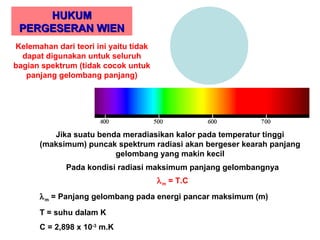
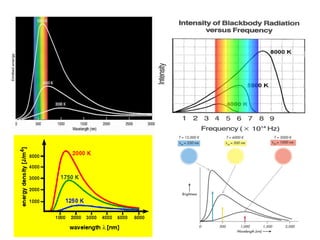
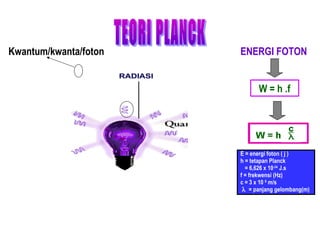
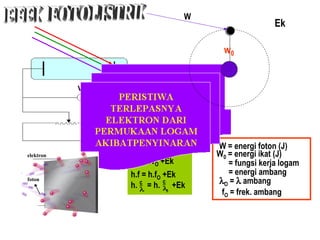
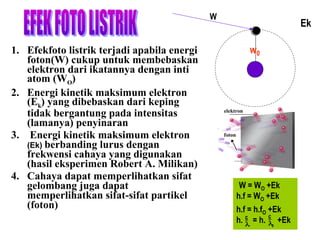
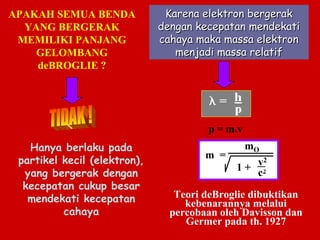
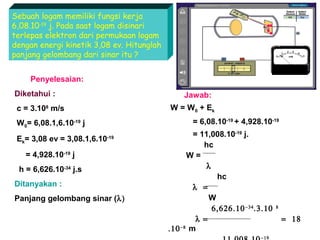
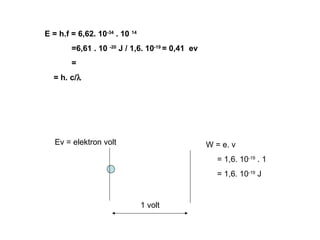
Standar kompetensi ini membahas analisis keterkaitan berbagai besaran fisika dalam paradigma kuantum dan relativitas, mencakup gejala kuantum seperti radiasi benda hitam, efek fotoelektrik, kompton, dan de Broglie. Kompetensi dasar menganalisis secara kualitatif gejala kuantum termasuk sifat dan hukum radiasi benda hitam.

2. Standar Kompetensi : 9.
Menganalisis keterkaitan antara berbagai besaran fisis pada gejala
kuantum dan menerapkan batas-batas berlakunya relativitas Einstein
dalam paradigma fisika modern.
Kompetensi dasar
9.1 Menganalisis secara kualitatif gejala kuantum yang mencakup
hakikat dan sifat-sifat radiasi benda hitam, serta penerapannya.
Idikator
• Menganalisis dan menginterpretasi data empiris tentang
radiasi benda hitam.
• Memformulasikan hipotesa Planck
• Memformulasikan hukum pergeseran Wien dan hukum
Stefan Boltzmann berdasarkan hipotesa Planck
• Mengaplikasikan sifat-sifat radiasi benda hitam untuk
mengukur suhu matahari dan suhu bintang

4. 1. MENGISI RUANG
2. MEMILIKI λ
1. MENEMPATI
HK. STEFAN –
BOLTZMANN
HK. PERGESERAN WIEN
TEORI
RELEIGH DAN
JEANS
TEORI PLANCK
EKSPERIMEN
R.A. MILIKAN2.
SESUAI VOLUME
PANJANG
MEMILIKI GELOMBANG
DE BROGLIE
MOMENTUM
TEORI
EINSTEIN
EFEK
COMPTON
PERCOBAAN
DAVISSON
DAN GERMER

5. BENDA HITAM
(BLACK BODY)
Kemampuan menyerap
energi maksimal ( e = 1 )
Kemampuan memancarkan
energi maksimal ( e = 1 )

6. Energi yang dipancarkan atau
diserap per satuan waktu per
satuan luas ( J.s-1.m-2 ),
dirumuskan :
E=e.τ .T
4
E = Laju perpindahan kalor atau
banyak kalor per satuan waktu
(J/s atau kal/s)
e = emisivitas permukaan (koefisien
pancara/serapan benda)
τ = tetapan Stefan = 5,67.10-8 watt.m-2.K-4
T = suhu mutlak (K)
Energi yang dipancarkan atau diserap
per satuan waktu per satuan luas dapat
juga dirumuskan :
E=
P
A
E = Laju perpindahan kalor atau
banyak kalor per satuan waktu
(watt.m-2)
P = Daya pancar ( watt )
A = luas permukaan benda (m2)
P = E . A = e . τ . T4 . A Daya pancar

7. CONTOH SOAL
Sebuah benda memiliki permukaan
hitam sempurna, 270 C. Berapa besarnya
energi yang dipancarkan tiap satuan
waktu tiap satuan luas permukaan benda
itu ?
DIKETAHUI :
e = 1 (benda hitam sempurna)
T = 27 + 273 = 300 K
τ = 5,67.10-8 watt.m-2.K-4
DITANYAKAN : E = …. ?
JAWAB :
Penyelesaian:
E = e . τ . T4
= 1 x 5,67.10-4 x (300)4
= 5,67.10-8 x 81.108
= 459,27.10-4 watt/m2
Sebuah bola memiliki jari-jari 20 cm
dipanaskan sampai suhu 500 K,
sedangkan benda-benda disekitarnya bersuhu 300 K. Berapa daya
yang diperlukan untuk mempertahankan suhu bola jika permukaannya memiliki emisivitas ½ ?
DIKETAHUI :
e=½
r = 20 cm = 0,2 m
T1 = 300 K ; T2 = 500 K
τ = 5,67.10-8 watt.m-2.K-4
DITANYAKAN : Daya = P = …. ?
JAWAB :
Penyelesaian:
Luas bola =A= 4π.r2 = 4x3,14x (0.2)2
A = 0,5 m2
Daya pancar tiap satuan luas
E = e . τ . ∆T4
= ½ x 5,67.10-8 x (200)4
= 1542.10-4 watt/m2
Daya yang diperlukan
P = E.A= 1542.10-4 x 0,5 = 0,0771 watt

8. HUKUM
PERGESERAN WIEN
Kelemahan dari teori ini yaitu tidak
dapat digunakan untuk seluruh
bagian spektrum (tidak cocok untuk
panjang gelombang panjang)
Jika suatu benda meradiasikan kalor pada temperatur tinggi
(maksimum) puncak spektrum radiasi akan bergeser kearah panjang
gelombang yang makin kecil
Pada kondisi radiasi maksimum panjang gelombangnya
λ m = T.C
λ m = Panjang gelombang pada energi pancar maksimum (m)
T = suhu dalam K
C = 2,898 x 10-3 m.K

9. RELEIGH DAN JEANS MENGOREKSI TEORI
WIEN MELALUI EKSPERIMENNYA AKAN
TETAPI HASIL EKSPERIMEN HANYA
COCOK PADA DAERAH SPEKTRUM
CAHAYA TAMPAK SEDANGKAN UNTUK
DAERAH PANJANG GELOMBANG PENDEK
TIDAK COCOK. KEGAGALAN INI DIKENAL
DENGAN BENCANA ULTRAVIOLET

13. E = e . τ . T4
E=
P
A
P = E . A = e . τ . T4 . A
λm.T= C

15. KESIMPULAN TEORI WIEN
• BENDA YANG BERADIASI
MEMANCARKAN ENERGI DALAM
BENTUK GELOMBANG

16. Kwantum/kwanta/foton
ENERGI FOTON
RADIASI
W = h .f
E = energi foton ( j )
h = tetapan Planck
= 6,626 x 10-34 J.s
f = frekwensi (Hz)
c = 3 x 10 8 m/s
λ = panjang gelombang(m)

17. W
Ek
w0
RADIASI
elektron
W = WO +Ek
h.f = WO +Ek
foton
h.f = h.fO +Ek
c
h. c = h. λ0 +Ek
λ
W = energi foton (J)
W0 = energi ikat (J)
= fungsi kerja logam
= energi ambang
λO = λ ambang
fO = frek. ambang

18. W
1. Efekfoto listrik terjadi apabila energi
foton(W) cukup untuk membebaskan
elektron dari ikatannya dengan inti
atom (WO)
2. Energi kinetik maksimum elektron
(Ek) yang dibebaskan dari keping
tidak bergantung pada intensitas
(lamanya) penyinaran
3. Energi kinetik maksimum elektron
(Ek) berbanding lurus dengan
frekwensi cahaya yang digunakan
(hasil eksperimen Robert A. Milikan)
4. Cahaya dapat memperlihatkan sifat
gelombang juga dapat
memperlihatkan sifat-sifat partikel
(foton)
Ek
w0
RADIASI
elektron
foton
W = WO +Ek
h.f = WO +Ek
h.f = h.fO +Ek
c
h. c = h. λ0 +Ek
λ

19. Cahaya dari sinar ultra violet dengan
panjang gelombang 2500 angstrum
dikenakan pada permukaan logam
kalium. Jika fungsi kerja logam kalium
2,21 ev, hitunglah berapa elektron volt
(ev) energi kinetik dari elektron yang
keluar dari permukaan logam kalium.
Penyelesaian:
Diketahui :
c = 3.108 m/s
λ = 2500 angstrum = 25.10-8 m
f = c/ λ = 3.108/25.10-8= 1,2.1015 hz
W0= 2,21 ev = 2,21.1,6.10-19
= 3,536.10-19 j
h = 6,626.10-34 j.s
Ditanyakan :
Energi kinetik elektron (Ek)
Jawab: W = W0 + Ek
Ek = W - W 0
= h.f - 3,536.10-19
= 6,626.10-34.1,2.1015- 3,536.10-19
= 4,415.10-19 j.
4,415.10-19
=
= 2,76 ev
1,6.10-19

20. Sebuah logam memiliki fungsi kerja
6,08.10-19 j. Pada saat logam disinari
terlepas elektron dari permukaan logam
dengan energi kinetik 3,08 ev. Hitunglah
panjang gelombang dari sinar itu ?
Penyelesaian:
Diketahui :
Jawab:
W = W0 + Ek
c = 3.108 m/s
= 6,08.10-19 + 4,928.10-19
W0= 6,08.1,6.10-19 j
Ek= 3,08 ev = 3,08.1,6.10
-19
= 4,928.10-19 j
h = 6,626.10-34 j.s
Ditanyakan :
Panjang gelombang sinar (λ)
= 11,008.10-19 j.
hc
W=
λ
hc
λ =
W
6,626.10 −34 .3.10
λ =
.10 −8 m
−19
8
= 18

21. Foton hambur( λ’ )
E = mo.c
2
Foton datang( λ )
E’ = h.f’
E = h.f
θ
P =0
Elektron hambur
λ = panjang gelombang foton sebelum tumbukan
λ’ = panjang gelombang foton setelah tumbukan
h = tetapan Planck = 6,626 x 10 –34 J.s
c = kecepatan cahaya = 3 x 10 8 m/s
m0 = massa diam elektron
θ = sudut hamburan elektron

22. Pada percobaan efek compton
digunakan sinar X dengan panjang
gelombang 0,1 angstrum. Sinar X
menumbuk elektron dan terhambur
dengan sudut sebesar 900. Jika
massa diam elektron 9,1.10-31 kg,
berapa panjang gelombang elektron
yang terhambur ?
Jawab:
h
λ' − λ =
( 1 − cosθ )
m0c
Penyelesaian:
Diketahui :
c = 3.108 m/s
λ = 0,1 angstrum = 10-11 m
m0= 9,1.10-31 kg
θ = 900
h = 6,626.10-34 j.s
Ditanyakan : Panjang gelombang
terhambur (λ')
6,626.10-34
λ' − λ =
cos90)
( 1 −
9,1.10-31.3.108
= 2,43.10-12
λ' = 2,43.10-12 + λ
= 2,43.10-12 + 10-11
= 1,243.10-11 m

23. Pada percobaan efek compton
digunakan sinar X dengan frekwensi
3.1019 hz. Pada saat menumbuk
elektron sinar ini terhambur dengan
sudut 600. Jika massa elektron diam
9,1.10-31 kg, hitunglah berapa
frekwensi dari sinar yang terhambur.
Penyelesaian:
Diketahui :
c = 3.108 m/s
f = 3.1019 hz
c
3.108
λ= =
= 10-11 m
f
3.1019
m0= 9,1.10-31 kg
θ = 600
h = 6,626.10-34 j.s
Ditanyakan : frekwensi sinar X
terhambur (f')
Jawab:
h
λ' - λ =
( 1 - cosθ )
m0c
6,626.10-34
λ' − λ =
cos60)
(19,1.10-31.3.108
= 2,43.10-12 ( 1 - 0,5)
= 1,215.10-12
λ' = 1,215.10-12 + λ
= 1,215.10-12 + 10-11
= 1,1215.10-11 m
c
3.108
f'=
=
λ'
1,1215.10-11
= 2,68.1019 hz

24. v
Bergerak lurus dengan
momentum p = m.v
m
v
m
Menurut deBroglie partikel
bergerak seperti gelombang ,
dengan demikian partikel pada
saat bergerak selain memiliki
momentum (p) juga memiliki
panjang gelombang( λ)
HUBUNGAN
ANTARA
λ MOMENTUM ( p )
DENGAN
PANJANG
GELOMBANG (λ)
λ = panjang
gelombang
deBroglie (m)
p = momentum (N.s)
h = tetapan Planck
= 6,626 x 10-34 J.s

25. Hitunglah panjang gelombang de
Broglie dari elektron yang bergerak
dengan kecepatan 2,4.108 m/s,
dengan menggunakan teori :
a. non relativistik b. relativistik
massa elektron diam 9,1.10-31 kg
Penyelesaian:
Diketahui :
v = 2,4.108 m/s = 0,8 c
m0= 9,1.10-31 kg; h = 6,626.10-34 j.s
Ditanyakan : panjang gelombang
deBroglie (λ)
Jawab:
a). dengan teori non relativistik,
berarti selama elektron bergerak
massanya tetap m = m0
h
6,626.10-34
λ =
=
mv
9,1.10-31.2,4.108
= 3,304.10-12 m
b). dengan menggunakan teori relativistik,
massa elektron berubah saat bergerak
m0
m=
; v2/c2 = (0,8c)2/c2 = 0,64
1 - v2/c2
h
h
λ =
=
mv
m0 . v
1 - v2/c2
h 1 - v2/c2 6,626.10-34 1 - 0,64
λ =
=
m0 . v
9,1.10-31.2,4.108
6,626.10-34.0,6
λ =
= 1,82.10-12 m
2,184.10-22

26. APAKAH SEMUA BENDA
YANG BERGERAK
MEMILIKI PANJANG
GELOMBANG
deBROGLIE ?
Karena elektron bergerak
dengan kecepatan mendekati
cahaya maka massa elektron
menjadi massa relatif
p = m.v
Hanya berlaku pada
partikel kecil (elektron),
yang bergerak dengan
kecepatan cukup besar
mendekati kecepatan
cahaya
m =
mO
v2
1 + c2
Teori deBroglie dibuktikan
kebenarannya melalui
percobaan oleh Davisson dan
Germer pada th. 1927

27. APLIKASI DARI TEORI deBROGLIE
PADA MIKROSKOP ELEKTRON
DIMANA CAHAYA DIGANTI
DENGAN ELEKTRON

28. •RUMUS WIEN HANYA BERLAKU PADA SPEKTRUM
GELOMBANG PENDEK
•TEORI RELEIGH DAN JEINS HANYA BERLAKU PADA
SPEKTRUM CAHAYA TAMPAK.
•CAHAYA MEMILIKI SIFAT KEMBAR (DUALISME)
YAITU PADA KONDISI TERTENTU MEMILIKI SIFAT
PARTIKEL DAN PADA KONDISI LAIN MEMILIKI
SIFAT GELOMBANG. AKAN TETAPI KEDUA SIFAT
TERSEBUT TIDAK MUNGKIN MUNCUL PADA SAAT
YANG SAMA
•PERCOBAAN COMPTON MEMBUKTIKAN BAHWA
CAHAYA MEMILIKI SIFAT PARTIKEL
•EKSPERIMEN DAVISON DAN GERMER
MEMBUKTIKAN ASUMSI DARI deBROGLIE BAHWA
PARTIKEL DAPAT MENUNJUKKAN SIFAT
GELOMBANG

30. Sebuah logam memiliki fungsi kerja
6,08.10-19 j. Pada saat logam disinari
terlepas elektron dari permukaan logam
dengan energi kinetik 3,08 ev. Hitunglah
panjang gelombang dari sinar itu ?
Penyelesaian:
Diketahui :
Jawab:
W = W0 + Ek
c = 3.108 m/s
= 6,08.10-19 + 4,928.10-19
W0= 6,08.1,6.10-19 j
Ek= 3,08 ev = 3,08.1,6.10
-19
= 4,928.10-19 j
h = 6,626.10-34 j.s
Ditanyakan :
Panjang gelombang sinar (λ)
= 11,008.10-19 j.
hc
W=
λ
hc
λ =
W
6,626.10 −34 .3.10
λ =
.10 −8 m
−19
8
= 18

36. E = h.f = 6,62. 10-34 . 10 14
=6,61 . 10 -20 J / 1,6. 10-19 = 0,41 ev
=
= h. c/λ
Ev = elektron volt
W = e. v
= 1,6. 10-19 . 1
= 1,6. 10-19 J
1 volt