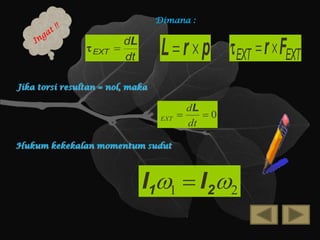
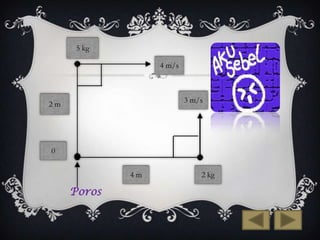
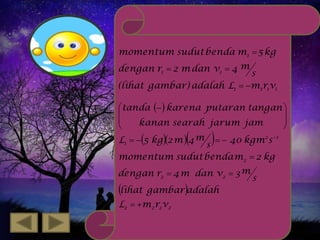
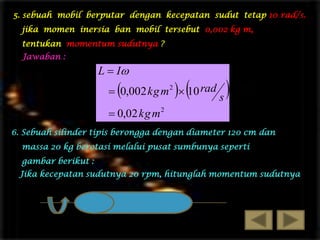
Dokumen ini membahas mengenai momentum sudut, menyusun pengertian, rumus, dan hukum kekekalan momentum. Momentum sudut didefinisikan sebagai hasil kali antara momen inersia dan kecepatan sudut, serta memiliki karakteristik sebagai besaran vektor. Contoh soal di dalamnya menunjukkan aplikasi konsep ini dalam fisika, termasuk perhitungan dan analogi dengan gerak linear.

1. Momentum Sud
Disusun oleh :
Rima Indasari MK
XII. Ipa
9962668608

2. Daftar Isi
Momentum pada
Pengertian
Vektor
Momentum Sudut
Hukum Kekekalan
momentum
D
A
F
T
A
R
P
U
S
T
A
K
A
ballerina
Hubungan
momentum
Contoh soal !!

3. A. Pengertian
Momentum sudut merupakan momentum yang
dimiliki benda-benda yang melakukan gerak rotasi.
Momentum sudut sebuah partikel yang berputar
terhadap sumbu putar didefenisikan sebagai hasil kali
Momentum linear partikel tersebut terhadap jarak
partikel ke sumbu putarnya.

4. Setelah mengenal besaran momentum linear yang dinyatakan
Oleh P = m . V pada gerak rotasi, yang analog dengan momentum
linear adalah Momentum sudut. Massa analog dengan momen
inersia,kecepatan linear analog dengan kecepatan sudut, maka
Momentum sudut L sama dengan hasil Kali momen inersia I
dengan kecepatan w.
L  I
Seperti halnya momentum linear, momentum sudut juga
merupakan suatu besaran Vektor. Arah momentum
sudut L dari suatu benda yang berputar diberikan oleh
Aturan tangan kanan; putar keempat jari yang dirapatkan
sesuai dengan arah gerak Rotasi, maka arah tunjuk ibu jari
menyatakan arah vektor momentumsudut.

5. Jika lengan torsi terhadap poros r dan kecepatan
linear v benda diberikan, Maka Momentum sudut L
dapat dihitung dengan persamaan sebagai berikut:
v
I  m r dan   , sehingga
r
2 v
L  I  m r  
r
Lmr v
2



6.  Momentum sudut L dari sebuah benda yang
berotasi tehadap sumbu tetap didefenisikan sbb:





L  r  p  m(r  v)
l  mvr sin 
 rp  rmv
 r p  r mv

7.  Perubahan momentum sudut terhadap waktu
diberikan oleh:
dL
d

r  p 
dt
dt
d
dr
dp 
r  p  
 p   r 

 


 dt
 
dt
dt 
 v  mv 
0
dL
dp
r
dt
dt
FEXT
dp

dt

8.  Perubahan momentum sudut terhadap waktu diberikan oleh:
dL
dp
r
dt
dt
dL
 r  FEXT
dt
Akhirnya diperoleh:
 EXT
dL

dt
FEXT
dp

dt
Analog dengan :

9. Arahnya dapat ditentukan dari ungkapan torka maupun
momentum sudut sebagai perkalian vektor dua dari dua vektor
lainnya. Rumus umumnya adalah :
 
  R F

Arah  tegak lurus budang yang dibentuk vektor R dan F dan
sesuai dengan majunya sekrup ketika diputar dari R ke F
  
L  R p
Arah L tegak lurus budang yang dibentuk vektor R
dan p dan sesuai dengan majunya sekrup ketika
diputar dari R ke p

10. Vektor Momentum Sudut
Momentum sudut dari sebuah benda yang berotasi
tehadap sumbu tetap adalah hasil kali dari momen
inersia benda dengan kecepatan sudut terhadap sumbu
rotasi tersebut.


L  I
Demikan juga dengan torsi (Hk II Newton untuk
gerak rotasi):




 dL d ( I )
d
 

I
 I
dt
dt
dt

11. Jika tidak ada torsi luar, L kekal. Artinya bahwa
hasil perkalian antara I dan w kekal
I   mi ri
L  I
2
L  I

12. Hukum Kekekalan Momen
Hukum Kekekalan Momentum Sudut menyatakan bahwa :
Jika Torsi total yang bekerja pada sebuah benda tegar = 0,
maka momentum sudut benda tegar yang berotasi bernilai konstan.
Momentum sudut dinotasikan dengan L, satuannya kg.m2/s
Pada gerak rotasi momen inersia I merupakan analogi dari massa
m dan ω merupakan analogi dari kecepatan linier v, maka rumus
momentum sudut untuk gerak rotasi dapat dituliskan :
p = m.v dan v = ω.r
maka dihasilkan
L  I

13. Keterangan :
L = momentum sudut dalam kg. m2/s
I = momen inersia dalam kg.m2
ω = kecepatan sudut dalam rad/s.
Hubungan momentum sudut dengan momen gaya
Analogi dengan hubungan impuls dan momentum maka hubungan
momentum sudut dengan momen gaya dapat diperoleh :
 dt  dl

14. Dimana :
 EXT
L  r  p  EXT  r  FEXT
dL

dt
Jika torsi resultan = nol, maka
EXT
dL

0
dt
Hukum kekekalan momentum sudut
I11  I22

15. Hukum kekekalan momentum terbagi atas 2 bagian yaitu :
Linear
oJika SF = 0, maka p konstan.
Rotasi
oJika St = 0, maka L konstan.
Defenisi & Penurunan
Untuk gerak linear sistem partikel berlaku
FEXT
dp

dt
Momentum kekal jika
FEXT  0
Bagaimana dng Gerak Rotasi?
Untuk Rotasi, Analog gaya F adalah Torsi 
Analog momentum p adalah momentum sudut
  r F
L r p

16. Kekekalan Momentum Sudut Pad
Tidak ada torka yang bekerja sehingga momentum
sudut kekal
L1  L2
I11  I 22
Merapatkan
Membuka
kaki dan
kaki dan
tangan
tangan
menyebabkan
menyebabkan
momen
momen
inersia
inersia
kecil
besar

17. Tidak ada torka yang bekerja
pada Bumi sehingga momentum
sudut Bumi tetap. Karena momen
inersia bumi tetap maka kecepatan
rotasi Bumi juga tetap.
Kecepatan rotasi Bumi bisa
berubah jika bumi ditabrak oleh
asteroid yang cukup besar yang
tidak mengarah ke pusat Bumi.
Tabrakan asteroid menghasilkan
torka yang mengubah momentum
sudut Bumi.

18. Hubungan Antara Momentum Sudut dan
Besar momentum sudut dan momentum linier memenuhi
L  pR sin 
dengan p momentum linier, R adalah jarak dari sumbu ke titik
di mana pusat momentum linier berada, dan  sudut yang
diukur dari perpanjangan R ke vektor momentum linier
“Laju perubahan momentum sudut terhadap waktu sebesar torsi yang bekerja
pada partikel tersebut”

19. Dua buah benda sedang
bergerak, tentukan besar dan
arah momentum sudut total
terhadap titik poros o.
Strategi :
Karena lengan torsi terhadap
poros o dan kecepatan linier
diberikan, maka momentum
sudut tiap benda sebaiknya
dihitung dengan persamaan
L=mrv

20. 5 kg
4 m/s
3 m/s
2m
0
4m
Poros
2 kg

21. momentum sudut benda m1  5 kg
dengan r1  2 m dan v1  4 m
s
(lihat gambar) adalah L1  m1r1v1
tanda   karena putaran tangan 




kanan searah jarum jam


L1  5 kg 2 m  4 m   40 kgm2 s 1
s
momentum sudut benda m2  2 kg


dengan r2  4 m dan v2  3 m
lihat
gambar adalah
L2  m2 r2 v2
s

22. tanda ( ) karena putaran tangan kanan 


 berlawanan arah jarum jam



L2   2 kg 4 m  3 m  24 kg m 2 s 1
s


momentum sudut total terhadap poros O adalah
 L  L1  L2
 40  24  16kg m 2 s 1
tanda negatif menyatakan bahwa
arah momentum sudut total terhadap
poros O adalah searah jarum jam.

23. Soal !!!!!
2. Seorang penari sepatu es memiliki momen inersia 4,0 m ketika
kedua lengannya terentang dan 1,2 kg m ketika kedua lengannya
merapat ketubuhnya. Penari mulai berputar pada kelajuan 1,8
putaran/sekon ketika kedua lengannya terentang . Berapa
kelajuan sudut ketika kedua lengannya merapat ketubuhnya ?
3. Sebuah meja putar terdiri dari sebuah cakram mendatar dengan
massa M dan jari-jari R dan berputar tanpa gesekan dengan
kelajuan tetap . Pada suatu waktu , setetes lem dengan massa
m= M/10 jatuh vertikal pada meja putar dan melekat disuatu titk
pada jarak r= 3R/4 dari poros. Tentukan kelajuan sudut putar
sekarang .

24. Jawaban :
2.Keadaan awal ketika kedua lengan terentang :
I1  4,0 kg m 2
1  1,8 putaran s
Keadaan akhir ketika kedua lengan merapat ketubuh :
2  .... ?
I 2  1,2 kg m 2
Kekekalan momentum :
L1  L2
I11  I 2 2
I1
2  1
I2
4,0 kg m 2

1,2 kg m 2
 6 putaran
 1,8 putaran 

s


s

25. 3. Diketahui :
m1  M
r1  R
1
1
2
momen inersia cakram I1  m1r1  MR2
2
2
kecepa tan sudut mula  mula : 1  
1

momentum sudut mula  mula : L1  1 I1    MR2 
2

M
3R
massa lem m2 
, melekat pada jarak dari poros r2 
10
4
Dengan demikian, momen inersia lem (lem dianggap sebagai
partikel) adalah :
2
M  3R  9MR2

2
I 2  m2 r2     
160
 10  4 

26. Sistem sekarang adalah (cakram + lem) sebagai satu sistem yang
bergerak dengan kecepatan Sudut
1  2  
Dengan menggunakan hukum kekekalan momentum dapat diperoleh :




L1  L2  L1  L2
Subtitusi 1    
2
1 I1  0  1 I1  2 I 2
1 I1  1 I1  2 I 2
1

  MR2 
1 I1
80 MR2
2
 

1 I1    I1    I 2   
2
2
I1  I 2
1 I1   I1  I 2 
 
80

89
1
9 MR
MR2 
2
160
80 MR  9 MR2

27. 4. Berapa momentum sudut bola 0,210 kg yang berotasi diujung tali
dan membentuk lingkaran dengan radius 1,01 m dengan laju
sudut 10,4 rad/s ?
I  mr 2
 0,210 kg 1,01m 
2
 0,214 kg m 2
L  I

 0,214 kg m 2  10,4 rad
m2
 2,226 kg
s
s

Jawaban :

28. 5. sebuah mobil berputar dengan kecepatan sudut tetap 10 rad/s.
jika momen inersia ban mobil tersebut 0,002 kg m,
tentukan momentum sudutnya ?
Jawaban :
L  I

 
 0,002 kg m 2  10 rad
s

 0,02 kg m 2
6. Sebuah silinder tipis berongga dengan diameter 120 cm dan
massa 20 kg berotasi melalui pusat sumbunya seperti
gambar berikut :
Jika kecepatan sudutnya 20 rpm, hitunglah momentum sudutnya

29. diketahui: d  120 cm  R  60 cm  0,6 m
m  20 kg
  20 rpm
di tan yakan: L.....?
  20 rpm 
20 rpm 1
 rps
60 s
3
2 rad

s
3
2
I  mR 2  20 0,6   7,2 kg m 2
m2
L  I  7,2 120  864 kg
s

30. Daftar Pustaka
Haryadi Bambang. 2008. fisika. IX. jakarta
www.google.com

31. THANK YOU