1. 統計学勉強会
第三回
@kingqwert

2. GLM

3. GLM概形
• g()は連結関数(リンク関数)
• 現実には非線形なので解析解は不可能
→ シミュレーションにより数値解を出す。

4. 正規線形モデル
• 行列表記
• 分散分析
– N(an)人の対象者をa水準からなる要因にランダムにn
人ずつ割りつけた場合
一般 主効 ランダム
効果 果 誤差

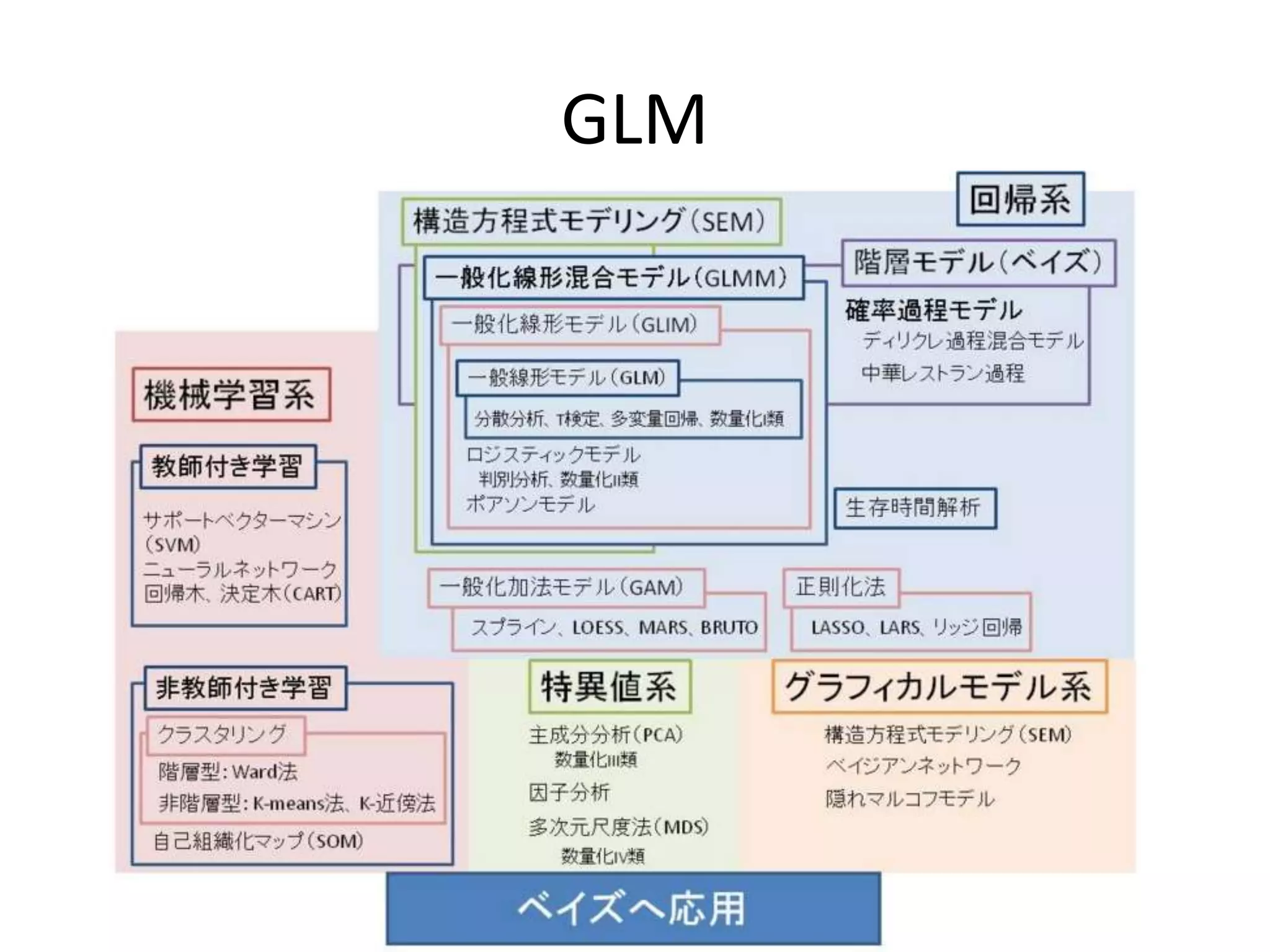
5. 回帰モデル
• 目的
– 結果変数に対する説明変数の関連の程度を回帰パラ
メーターを通して定量的に表現
• 線形モデル
– 未知パラメーターに関して線形
– 非線形モデル： y=a×exp(-bx)

6. 最小二乗法
• 残差平方和を最小にするように推定
– 残差＝観測値ー予測値
• 最小化

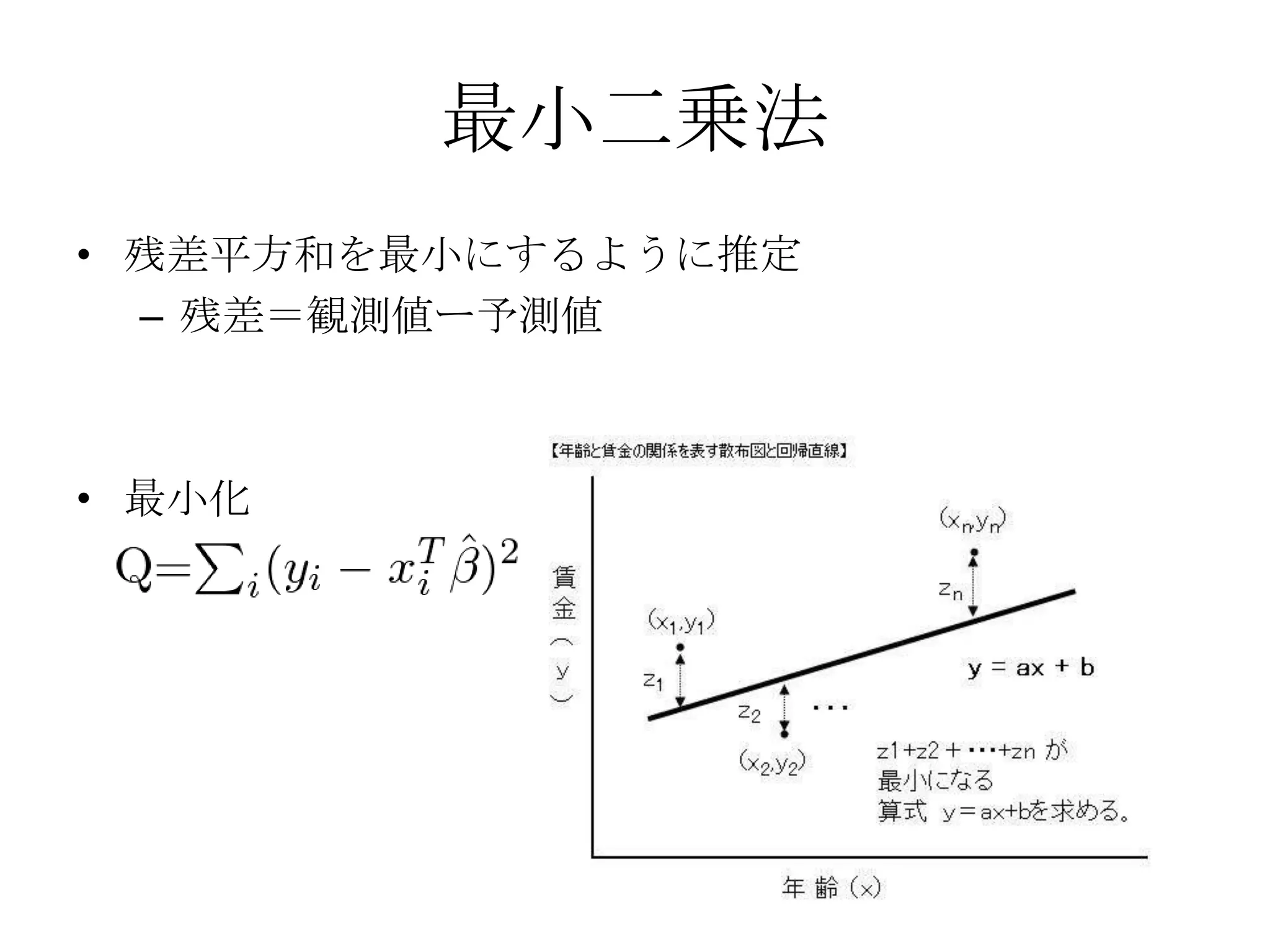
7. ガウス=マルコフの条件
• 誤差に関する仮定
– E(ε)=0
– V(ε)=σ^2 I
– 二次モーメントまでの制約のみ
• 普遍性
• 独立性
• 等分散性
• →ここまででBLUEになるよ
• 正規性は仮定しない→UMVU推定量に
– あらゆる不偏推定量の中で最小

8. ロジスティック回帰
• 回帰分析とは、
被説明変数
係数を推定
説明変数
13/02/12 機械学習勉強会＠本郷キャンパス 8

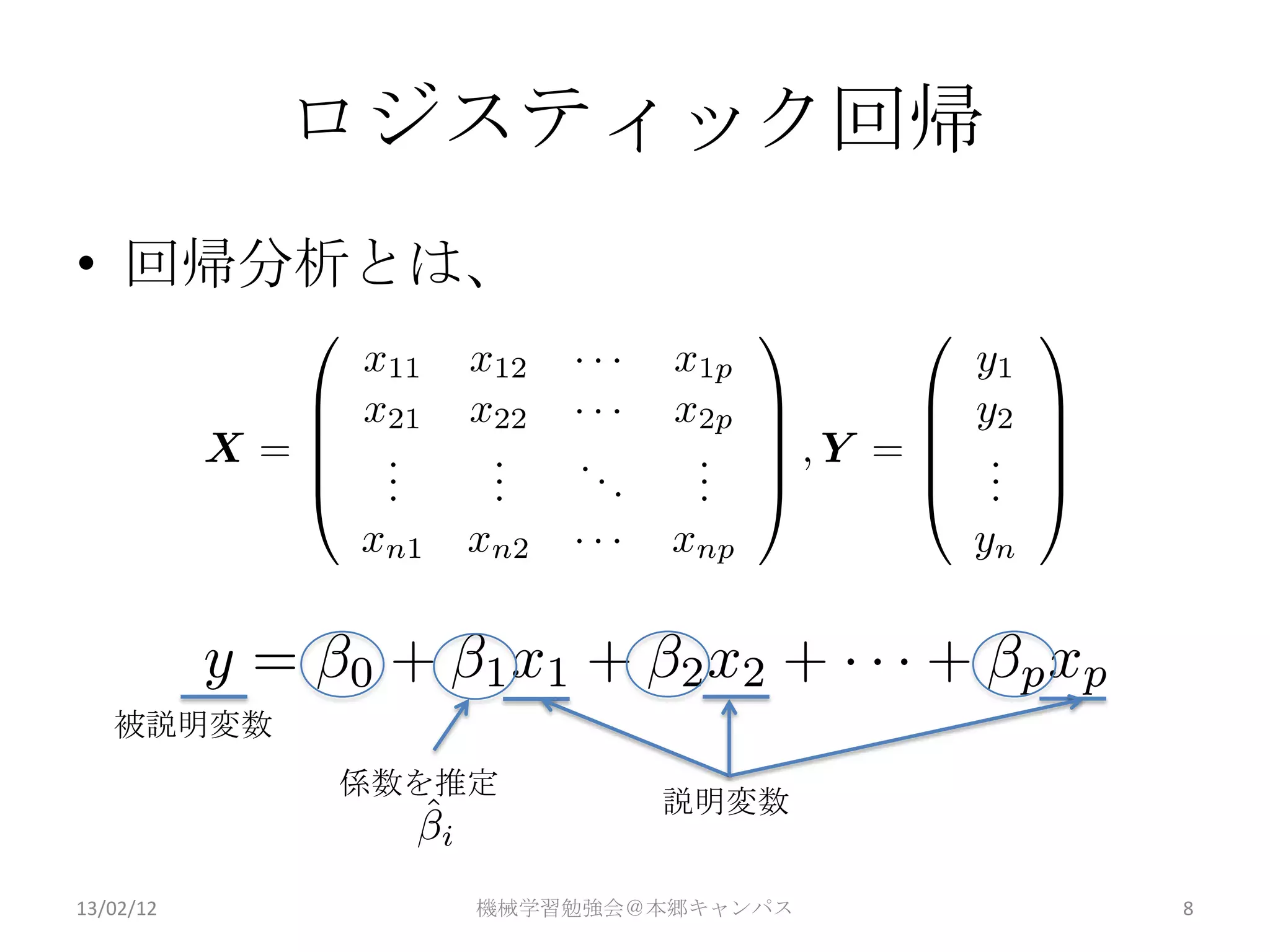
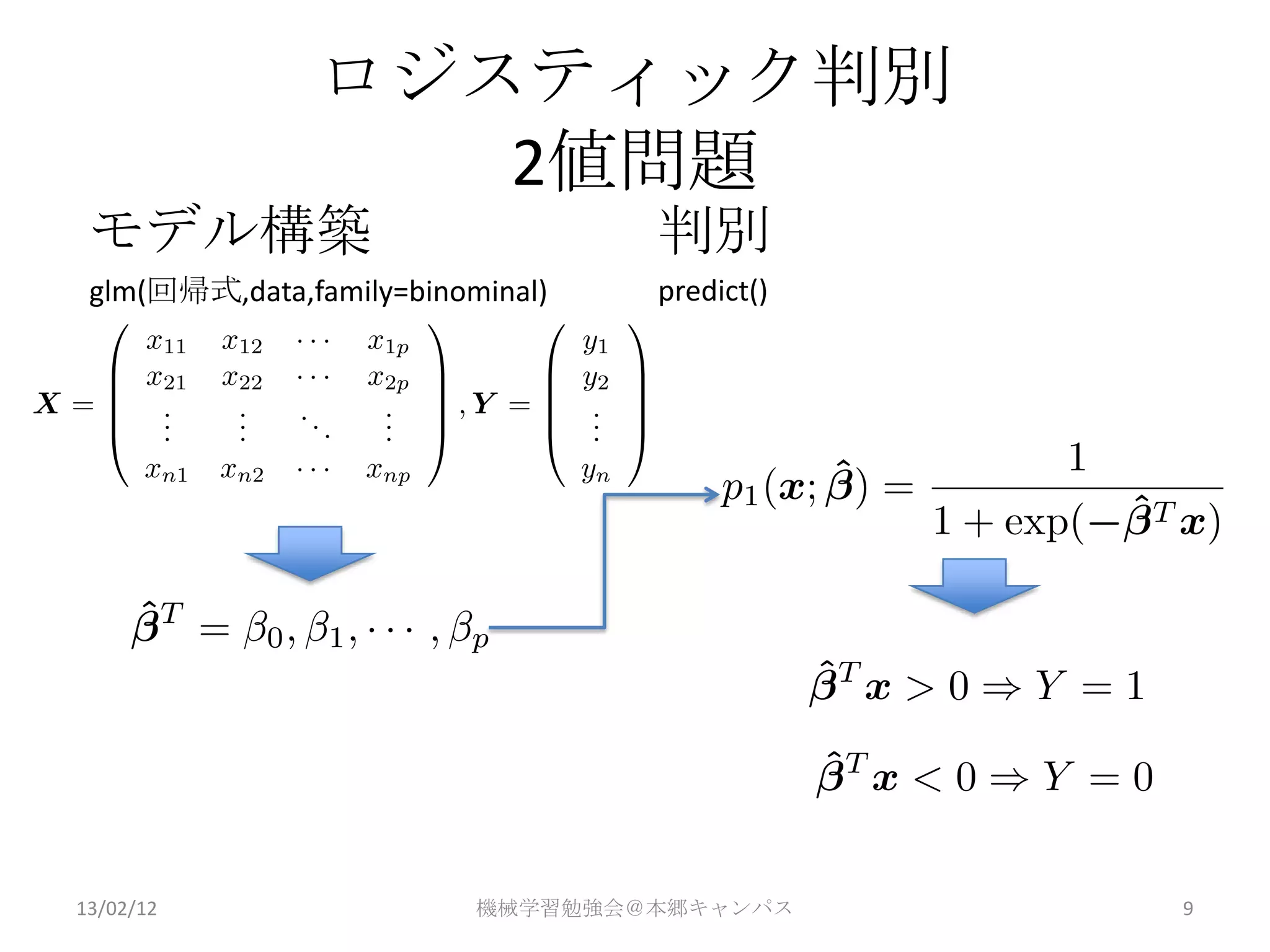
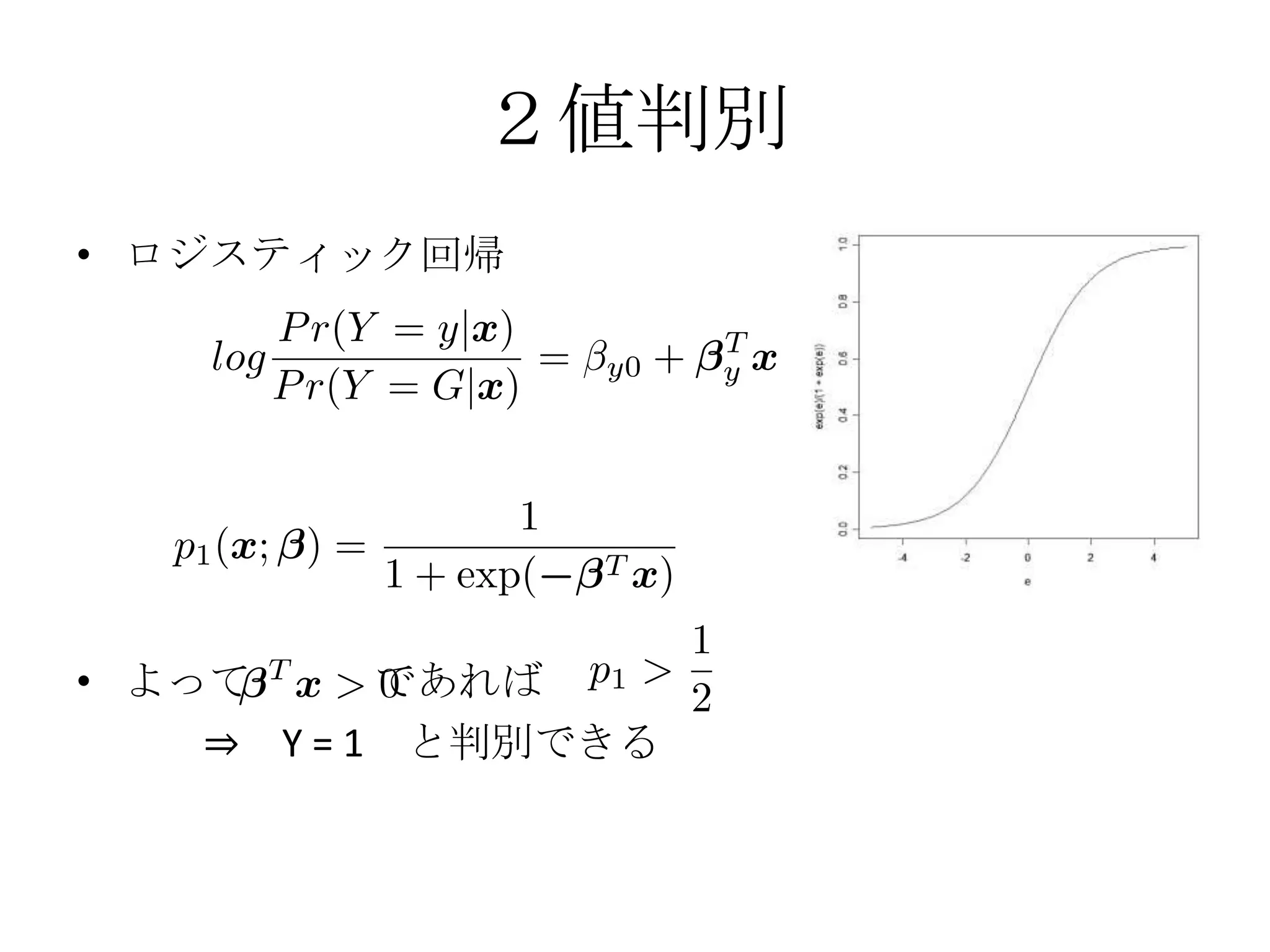
9. ロジスティック判別
2値問題
モデル構築 判別
glm(回帰式,data,family=binominal) predict()
13/02/12 機械学習勉強会＠本郷キャンパス 9

10. ２値判別
• ロジスティック回帰
• よって であれば
⇒ Y = 1 と判別できる

11. ポワソン/対数線形モデル