The document explains Lagrange's Mean Value Theorem (LMVT), outlining its conditions and providing geometrical interpretation as well as verification examples using different functions. It includes solutions to multiple problems verifying LMVT for specific mathematical functions, demonstrating how to find points where the tangent is parallel to the chord connecting endpoints. Additionally, it notes the applicability of LMVT and identifies when it is not applicable.

2. PREVIEW:
EXPERIENCED MATH TEACHER
• EXPLAIN LAGRANGE’S MEAN VALUE THEOREM
• IT’S GEOMETRICAL INTERPRETATION
BONUS:
DISCUSS A FEW GRADE 12 QUESTION PAPERS

3. Here, I will only be stating Lagrange’s Mean Value Theorem and not discussing the proof
LAGRANGE’S MEAN VALUE THEOREM states that
If a function f is
i). Continuous on [a,b]
ii) f is derivable on (a,b)
Then there exists at least one real number c ∈ 𝑎, 𝑏 𝑠𝑢𝑐ℎ 𝑡ℎ𝑎𝑡 𝑓′
𝑐 =
𝑓 𝑏 −𝑓(𝑎)
𝑏−𝑎

4. Geometrical interpretation of Lagrange’s Mean Value Theorem
Lagrange’s Mean Value Theorem states that there exists at least one point
lying between A and B, the tangent at which is parallel to the chord AB.
B
A
B

5. A
B

6. Question 1 (GRADE XII MATH)
VERIFY Lagrange’s Mean Value Theorem for the function f(x) = 𝑥3
− 5𝑥2
− 3𝑥 𝑖𝑛 [1,3]
i)f being a polynomial function is continuous in [1,3]
ii) 𝑓′
𝑥 = 3 𝑥2
− 10 𝑥 − 3
f is derivable on (1, 3 )

7. By lagrange’s Mean Value Theorem, there exists at least one c ∈ 1,3 𝑠𝑢𝑐ℎ 𝑡ℎ𝑎𝑡
𝑓′
𝑐 =
𝑓 3 − 𝑓(1)
3 − 1
3𝑐2 − 10𝑐 − 3 =
−27 + 7
2
3 𝑐2 − 10𝑐 − 3 = −10
3𝑐2 − 10𝑐 + 7 = 0

8. 3𝑐2
− 7𝑐 − 3𝑐 + 7 = 0
𝑐 3𝑐 − 7 − 3𝑐 − 7 = 0
3𝑐 − 7 𝑐 − 1 = 0
𝑐 =
7
3
, 1
𝑐 =
7
3
∈ (1,3)
Lagrange’s mean value theorem is satisfied

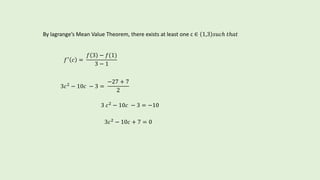
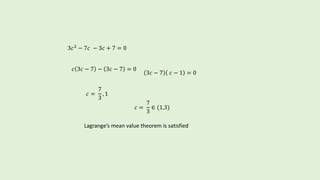
9. Question 2
Verify lagrange’s Mean Value Theorem for the function f(x) = sinx – sin 2x on [ 0,𝜋]
i) f being a trigonometric function is continuous on[ 0,𝜋]
ii) 𝑓′ 𝑥 = 𝑐𝑜𝑠𝑥 − 2 𝑐𝑜𝑠2𝑥
f is derivable on ( 0, 𝜋)
By lagrange’s theorem ∃ 𝑎𝑡 𝑙𝑒𝑎𝑠𝑡 𝑜𝑛𝑒 𝑣𝑎𝑙𝑢𝑒 𝑜𝑓 𝑐 ∈ 0, 𝜋 𝑠𝑢𝑐ℎ 𝑡ℎ𝑎𝑡

10. 𝑓′
𝑐 =
𝑓 𝜋 − 𝑓(0)
𝜋 − 0
cos c – 2 cos2c = 0
cos 𝑐 − 2 (2𝑐𝑜𝑠2 𝑐 − 1) = 0
cos 𝑐 − 4 𝑐𝑜𝑠2
𝑐 + 2 = 0

11. 4𝑐𝑜𝑠2 𝑐 − cos 𝑐 − 2 = 0
cos 𝑐 =
1 ± 33
8
cos c = 0.8431 or – 0.593
𝑐 = 32.530 𝑜𝑟 126.580 ∈ (0, 𝜋)
Hence lagrange’s Mean Value theorem satisfied

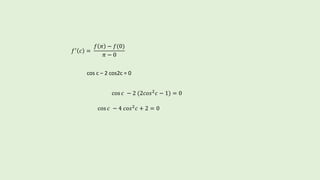
12. Question 3
Grade 12 math
Use lagrange’s mean value theorem to determine a point on the curve
𝑦 = 𝑥2 − 4 defined in [2,4], where the tangent is parallel to the chord joining
the endpoints of the curve
𝑓 𝑥 = 𝑥2 − 4
i) f is continuous on [2,4] being a polynomial function

13. 𝑓′
𝑥 =
𝑥
𝑥2 − 4
ii)
f is derivable on (2,4)
By lagrange’s Mean Value Theorem ∃ 𝑎𝑡 𝑙𝑒𝑎𝑠𝑡 𝑜𝑛𝑒 𝑝𝑜𝑖𝑛𝑡 𝑐 ∈ 2,4 𝑠𝑢𝑐ℎ 𝑡ℎ𝑎𝑡
𝑓′ 𝑐 =
𝑓 4 − 𝑓(2)
4 − 2 f(4 )= 12 = 2 3
f(2) = 0

14. 𝑐
𝑐2 − 4
=
2 3
2
𝑐2
= 3 (𝑐2
− 4)
𝑐2 = 3𝑐2 − 12
2𝑐2 = 12

15. 𝑐 = ± 6 = ±2.45
Lagrange’s mean value theorem is satisfied
𝑐 = 2.45 ∈ (2,4)
YOU are asked to determine the point at which the tangent is parallel to the chord
Students forget to do that.

16. 𝑦 = 𝑥2 − 4
𝑥 = 6
𝑦 = 2
𝑝𝑜𝑖𝑛𝑡 = ( 6, 2)

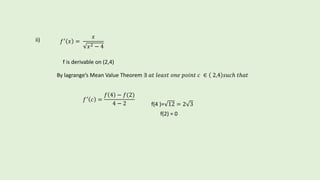
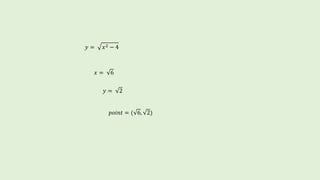
17. Question 4
Is lagrange’s Mean Value Theorem applicable for the function f(x) = 𝑥 𝑖𝑛 [−2,3]
𝑥 𝑖𝑠 𝑛𝑜𝑡 𝑑𝑒𝑟𝑖𝑣𝑎𝑏𝑙𝑒 𝑎𝑡 𝑥 = 0
lagrange’s mean value theorem is not applicable
https://www.youtube.com/watch?v=RNAdeCD1ncw&list=PL26
R7TjUyi8zDE3-OcadJuTKlXApnFJG6
GRADE 12 MATH : DIFFERENTIATION PLAYLIST VIDEOS FOR ISC, CBSE

18. For more videos on Differentiation, grade 12 math,
Subscribe to my channel