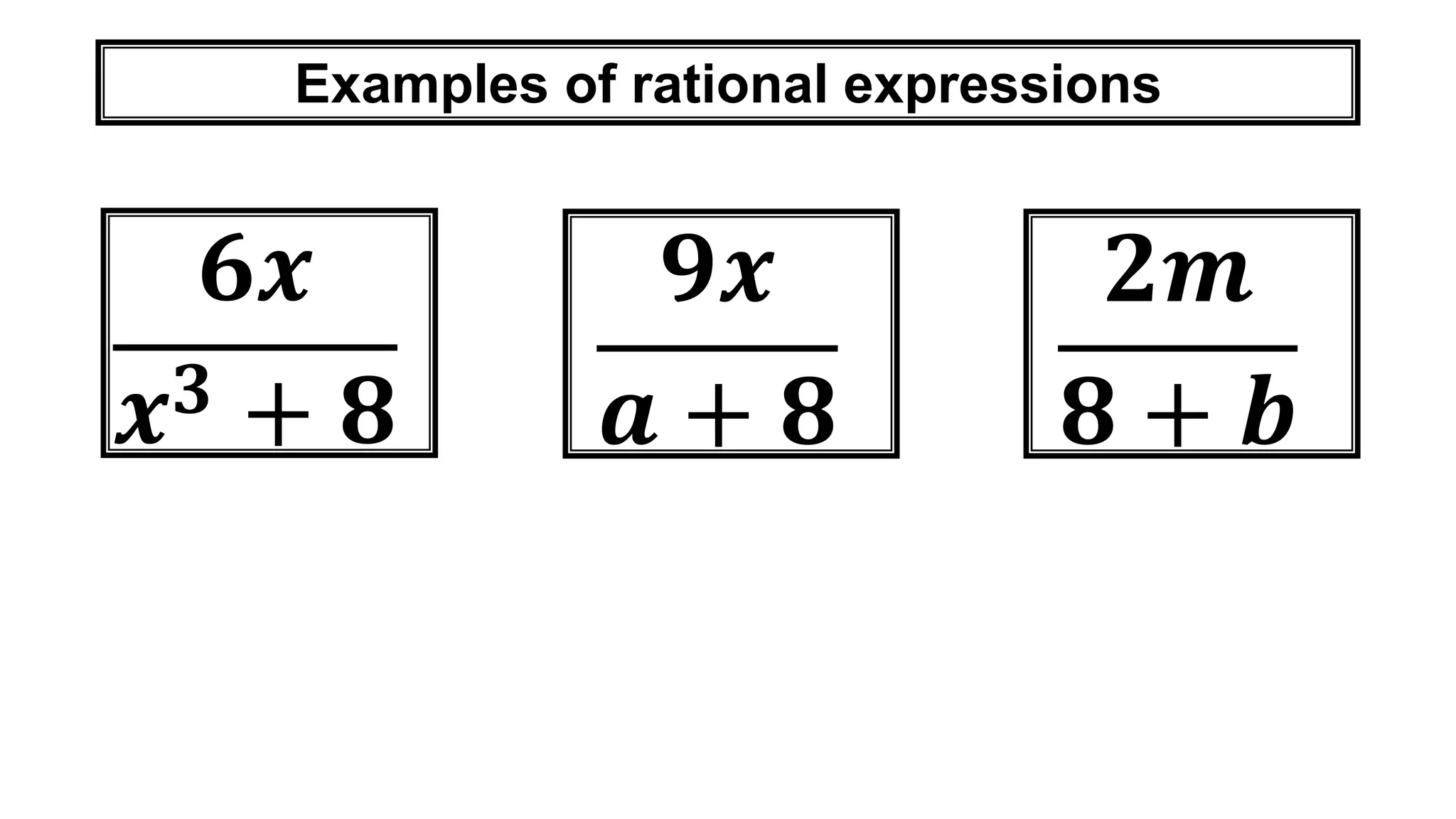
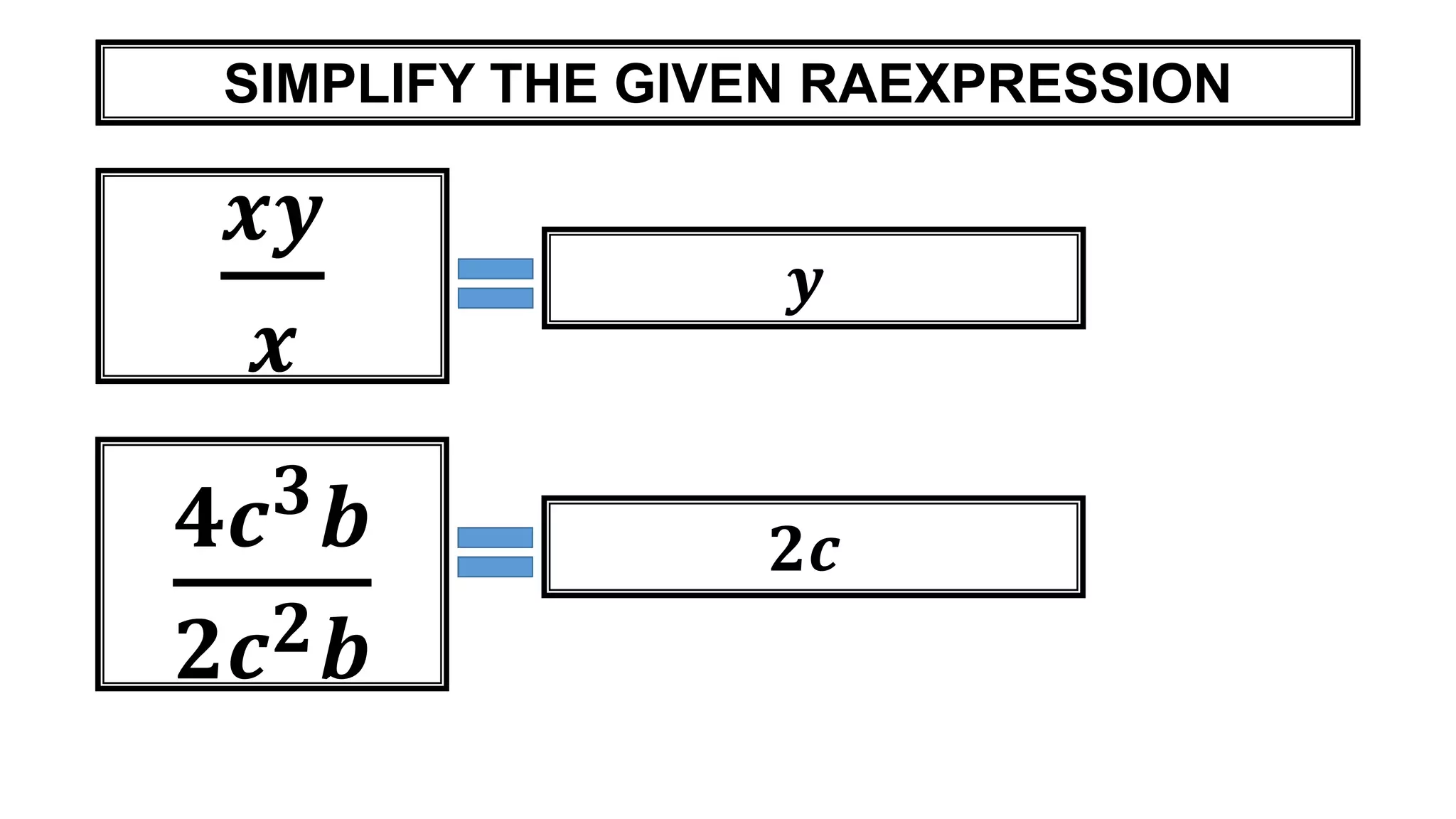
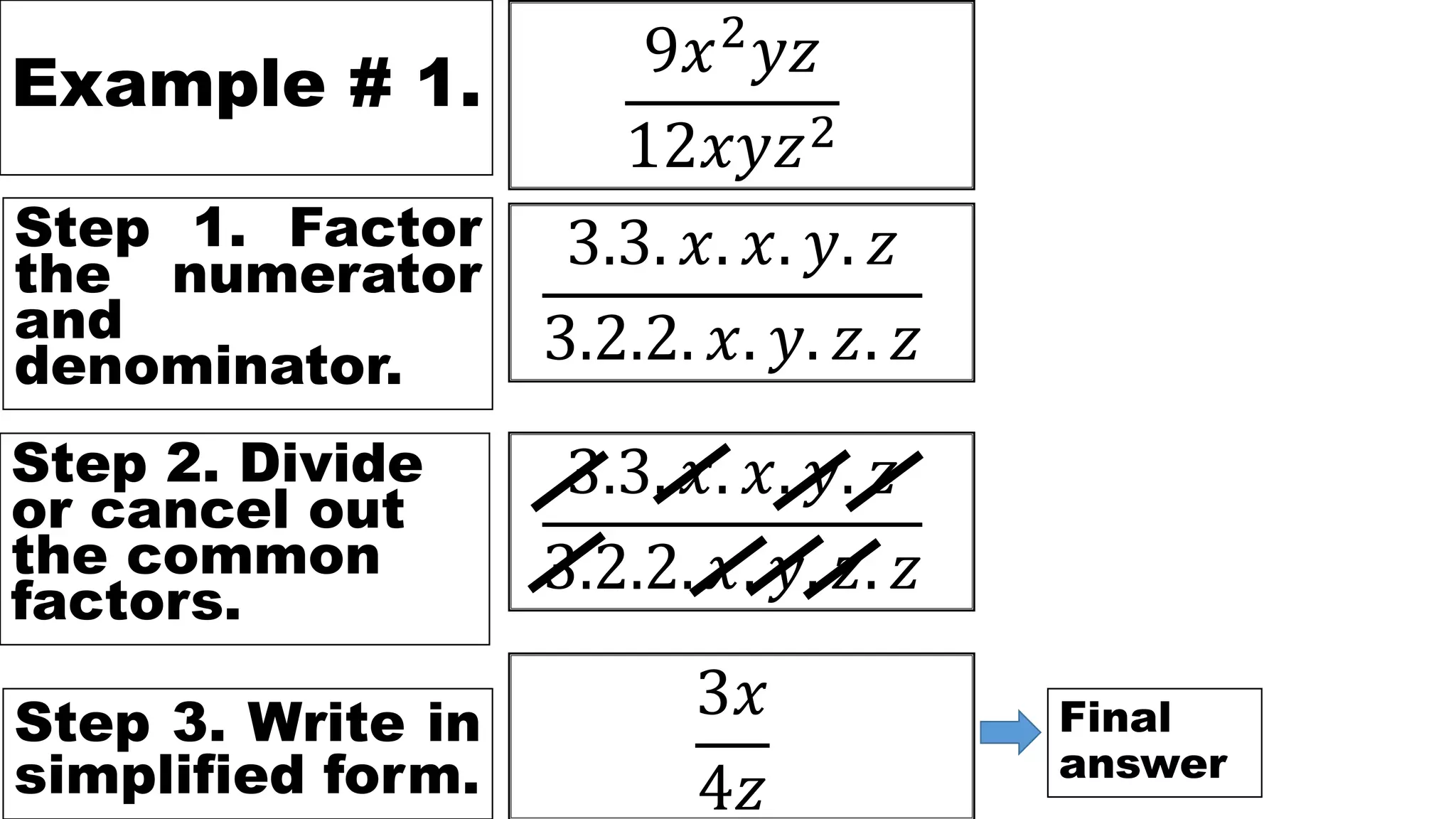
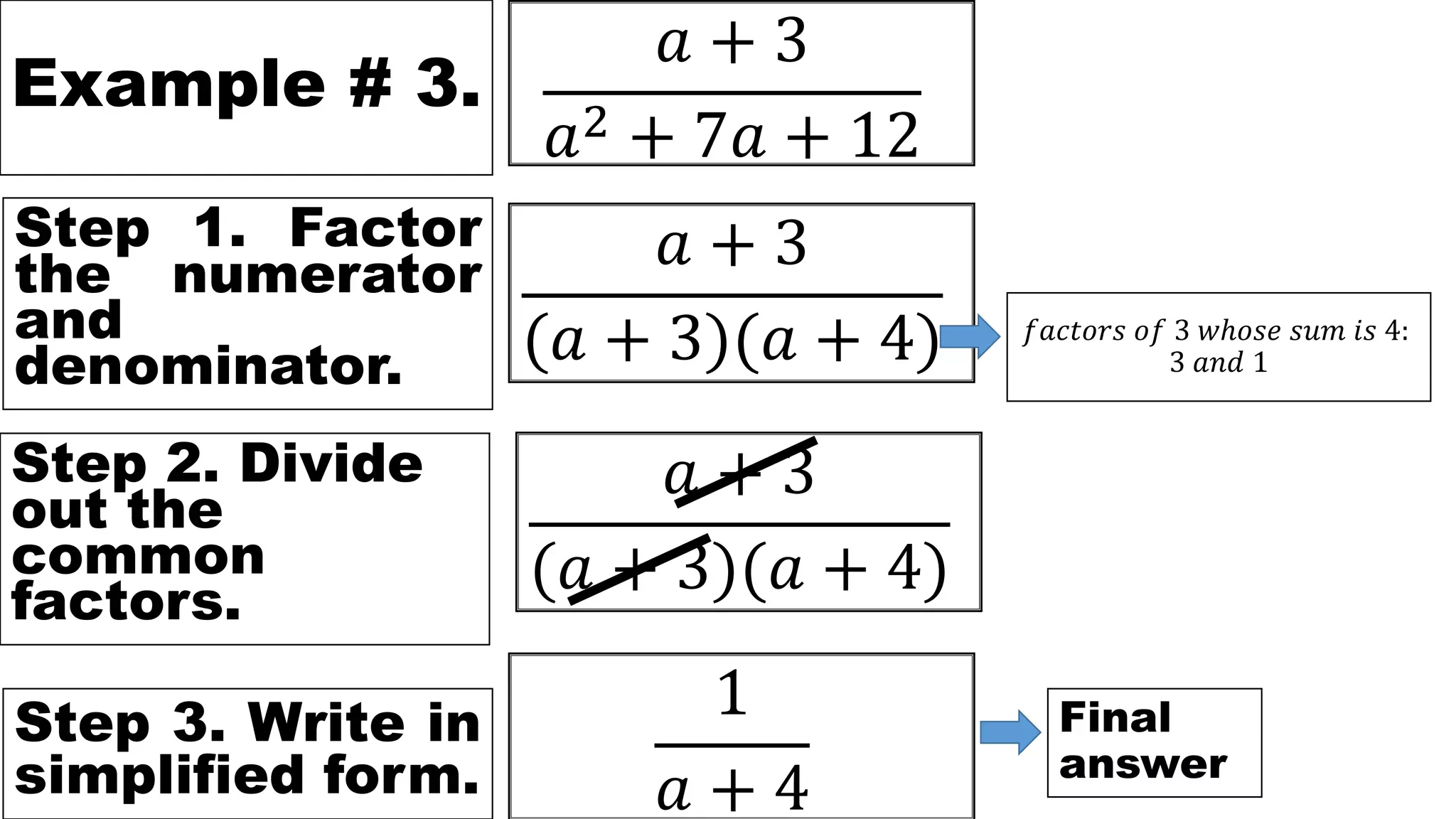
This document defines rational expressions as expressions that can be written in the form P/Q, where P and Q are polynomials and Q ≠ 0. It provides examples of rational expressions and explains the steps to simplify rational expressions: 1) factor the numerator and denominator, 2) divide out common factors, and 3) write the expression in simplified form. Three examples demonstrating these steps are included.

1. RATIONAL
ALGEBRAIC
EXPRESSIONS

2. Rational Expression
A rational expression is one variable
in an expression that can be written
in the form
𝑷
𝑸
where P and Q are
polynomials in one variable and
𝑸 ≠ 𝟎.

3. Examples of rational expressions
𝟔𝒙
𝒙 𝟑 + 𝟖
𝟗𝒙
𝒂 + 𝟖
𝟐𝒎
𝟖 + 𝒃

4. SIMPLIFY THE GIVEN RAEXPRESSION
𝒙𝒚
𝒙
𝒚
𝟒𝒄 𝟑 𝒃
𝟐𝒄 𝟐 𝒃
𝟐𝒄

5. • Factor the numerator and denominator.
• Divide out the common factors. In this case,
the common factors divide to become 1.
• Write in simplified form.

6. If a, b and c are nonzero numbers,
then ac
bc
a
b
=

7. Example # 1.
9𝑥2
𝑦𝑧
12𝑥𝑦𝑧2
Step 1. Factor
the numerator
and
denominator.
3.3. 𝑥. 𝑥. 𝑦. 𝑧
3.2.2. 𝑥. 𝑦. 𝑧. 𝑧
Step 2. Divide
or cancel out
the common
factors.
Step 3. Write in
simplified form.
3𝑥
4𝑧
Final
answer
3.3. 𝑥. 𝑥. 𝑦. 𝑧
3.2.2. 𝑥. 𝑦. 𝑧. 𝑧

8. Example # 2.
3𝑥2
+ 9𝑥
12𝑥3
Step 1. Factor
the numerator
and
denominator.
3𝑥 (𝑥 + 3)
3.2.2. 𝑥. 𝑥. 𝑥
3𝑥 (𝑥 + 3)
3.2.2. 𝑥. 𝑥. 𝑥
Step 2. Divide
out the
common
factors.
Step 3. Write in
simplified form.
(𝑥 + 3)
4𝑥2
Final
answer
3𝑥2 - 3 . 𝑥 . 𝑥 = x
9𝑥 - 3 . 3. 𝑥 = 3

9. Example # 3.
𝑎 + 3
𝑎2 + 7𝑎 + 12
Step 1. Factor
the numerator
and
denominator.
𝑎 + 3
(𝑎 + 3)(𝑎 + 4)
Step 2. Divide
out the
common
factors.
Step 3. Write in
simplified form.
1
𝑎 + 4
Final
answer
𝑓𝑎𝑐𝑡𝑜𝑟𝑠 𝑜𝑓 3 𝑤ℎ𝑜𝑠𝑒 𝑠𝑢𝑚 𝑖𝑠 4:
3 𝑎𝑛𝑑 1
𝑎 + 3
(𝑎 + 3)(𝑎 + 4)