Skip to main content
UploadLanguage (EN)Support
BusinessMobileSocial MediaMarketingTechnologyArt & PhotosCareerDesignEducationPresentations & Public SpeakingGovernment & NonprofitHealthcareInternetLawLeadership & ManagementAutomotiveEngineeringSoftwareRecruiting & HRRetailSalesServicesScienceSmall Business & EntrepreneurshipFoodEnvironmentEconomy & FinanceData & AnalyticsInvestor RelationsSportsSpiritualNews & PoliticsTravelSelf ImprovementReal EstateEntertainment & HumorHealth & MedicineDevices & HardwareLifestyle
Uploaded byZeinabAbohashima1
PPTX, PDF193 views

Quantum Search Algorithm and its Implementation using QisKit

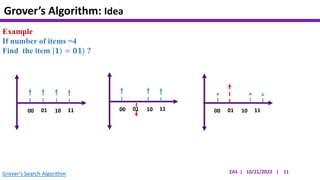
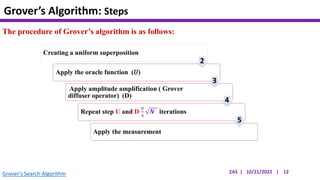
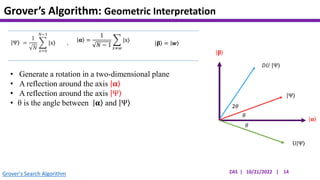
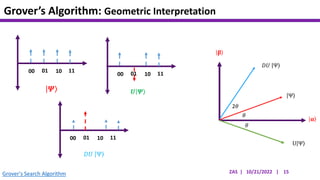
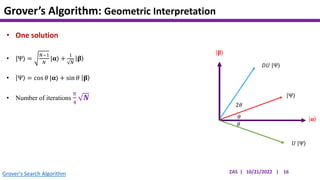
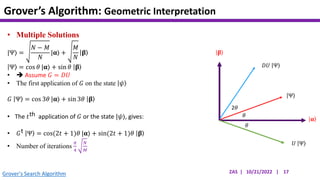
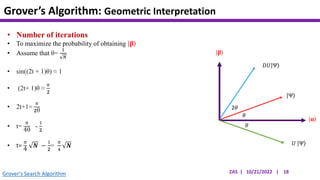
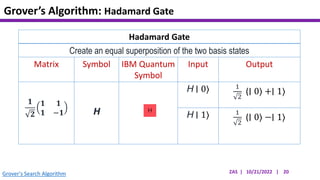
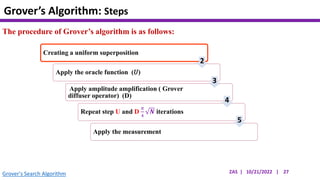
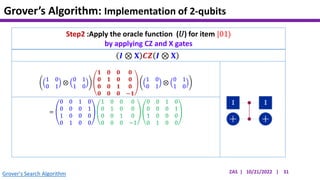
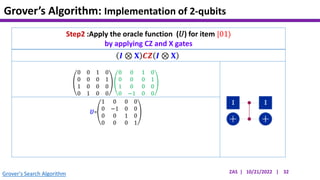
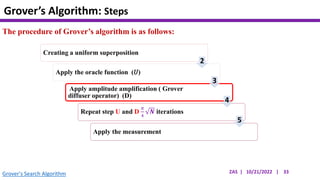
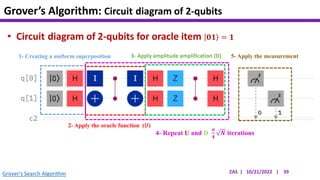
This document presents an implementation of Grover's quantum search algorithm using two qubits. Grover's algorithm allows searching an unstructured database with N elements using O(√N) iterations, compared to O(N) classically. The implementation first creates a uniform superposition of all states using Hadamard gates. It then applies an oracle function that inverts the amplitude of the target state. Amplitude amplification is performed using Grover's diffusion operator to increase the target state's probability. The process is repeated once, as the number of iterations is π√N/4 for this two-qubit example. Measurement then returns the target state with high probability.

Education◦
Download to read offline
https://dl.acm.org/doi/10.1145/237814.237866 Quantum Search Algorithm and its Implementation using QisKit To search in unstructured data with O( 𝐍) iterations Presented By: Zainab Abo-Hashima Grover's Algorithm : Grover, Lov K. "A fast quantum mechanical algorithm for database search." Proceedings of the twenty-eighth annual ACM symposium on Theory of computing. 1996.
1 Geometric Interpretation Circuit of 2-qubits Grover's algorithm Recap 2 3 5 Required Gates Grover's Search Algorithm 2 4 Agenda ZAS | 10/21/2022 | Implementation of 2-qubits Grover's algorithm
Grover's Search Algorithm 1- Recap: Unstructured Search , Quantum Oracle, and Amplitude Amplification 3 ZAS | 10/21/2022 |
Grover's Search Algorithm • Search problem: finding an element in an unstructured database • Suppose the search space consists of N elements • Find W minimum number of queries? • Classically, in the average case, we would have to evaluate all O(N/2) • In the worst case, we would have to evaluate all O(N) 4 10 55 …. w …. 3 99 0 1 2 3 4 5 6 N-1 Grover’s Algorithm: The Unstructured Search ZAS | 10/21/2022 | 4
Grover's Search Algorithm • In 1996, the computer scientist, Lov Grover, found a quantum algorithm for finding an item in an unstructured database of N items. Given : Assume we are given a function 𝑓(𝑥): {0,1}𝑛 → {0,1} Output : Find a target element (W) Grover’s algorithm claims to solve the problem with high probability in O( 𝑁) time. 4 10 55 ….. w ….. 3 99 0 0 0 0 1 0 0 0 Grover’s Algorithm: Overview ZAS | 10/21/2022 | 5
In simple terms, Grover’s algorithm consists of two parts: 1. Quantum Oracle 2. Amplitude Amplification ZAS | 10/21/2022 | 6
Grover's Search Algorithm 𝑓(𝑥) = 1, if 𝑥 = 𝑤 0, otherwise Grover’s Algorithm: Quantum Oracle Function • This oracle (black box) just flips the amplitude of the target element. • If the result is one, then it turns it negative direction • if the result is zero, then it turns it to positive direction (unchanged) • 𝑊ℎ𝑒𝑟𝑒 𝑡ℎ𝑒 𝑎𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑜𝑟𝑎𝑐𝑙𝑒 𝑖𝑠 |𝑥⟩ = (−1)𝑓(𝑥)|𝑥⟩ that satisfies: ZAS | 10/21/2022 | 7
Grover's Search Algorithm U X 𝑓(𝑥) = 1, if 𝑥 = 𝑤 0, otherwise q ⨁ f(x) X q Grover’s Algorithm: Quantum Oracle Function • This oracle (black box) just flips the amplitude of the target element. • If the result is one, then it turns it negative direction • if the result is zero, then it turns it to positive direction (unchanged) • 𝑊ℎ𝑒𝑟𝑒 𝑡ℎ𝑒 𝑎𝑐𝑡𝑖𝑜𝑛 𝑜𝑓 𝑜𝑟𝑎𝑐𝑙𝑒 𝑖𝑠 U|x〉|q〉 → |x〉|q ⨁ f(x)〉 that satisfies: ZAS | 10/21/2022 | 8
Grover's Search Algorithm Apply the oracle function (𝑈) 𝑈|x〉|q〉 → |x〉|q ⨁ f(x)〉 , |q〉 = 𝟏 𝟐 (∣ 𝟎⟩ −∣ 𝟏⟩ 𝑈 |x〉 |q〉 → |x〉| ( 1 2 (∣ 0⟩ −∣ 1⟩) ⨁ f(x)〉 = |x〉 ( 1 2 (∣ 0⟩⨁ f(x)⟩− ∣ 1⨁ f(x)⟩) =|x〉 ( 1 2 (∣ 0⨁ 1〉 −∣ 1⨁ 1⟩) =|x〉 ( 1 2 (∣ 1〉 −∣ 0⟩) = -|w〉 ( 1 2 (∣ 0〉 −∣ 1〉) 𝑖𝑓 𝑓 𝑥 = 1 𝑖𝑓 𝑓 𝑥 = 0 U|x〉 |q〉 → |x〉| ( 1 2 (∣ 0⟩ −∣ 1⟩) ⨁ f(x)〉 =|x〉 ( 1 2 (∣ 0⨁ f(x)〉 −∣ 1⨁ f(x)〉) =|x〉 ( 1 2 (∣ 0⨁ 0〉 −∣ 1⨁ 0〉) =|x〉 ( 1 2 (∣ 0〉 −∣ 1〉) Now, we can rewrite as U|𝑥⟩ = (−1)𝑓(𝑥)|𝑥⟩ Grover’s Algorithm: Quantum Oracle Function ZAS | 10/21/2022 | 9 Input Output X Y X ⊗ Y 0 0 0 0 1 1 1 0 1 1 1 0
Grover's Search Algorithm • Amplitude Amplification calculates the mean probability amplitude μ of all states and inverts the probability amplitudes around this mean. • Increases the amplitude of the target element, and decreases the amplitude of non target vector through iterations • Grover diffusion operator (D): Increasing the probability • Inversion about average • Rotating the vector Ψ towards 𝒘 (which is the solution). 𝐷 = 2|Ψ⟩⟨Ψ| − 𝐼 Grover’s Algorithm: Amplitude Amplification ZAS | 10/21/2022 | 10
Grover's Search Algorithm Grover’s Algorithm: Idea 11 ZAS | 10/21/2022 | Example If number of items =4 Find the item |𝟏⟩ = 𝟎𝟏⟩ ? 00 01 10 11 00 01 10 11 00 01 10 11
Grover's Search Algorithm The procedure of Grover’s algorithm is as follows: Creating a uniform superposition Apply the oracle function (𝑈) Apply amplitude amplification ( Grover diffuser operator) (D) Repeat step U and D 𝜋 4 𝑵 iterations Apply the measurement 2 3 4 5 Grover’s Algorithm: Steps 12 ZAS | 10/21/2022 |
Grover's Search Algorithm 2- Geometric Interpretation: One Solution, Multiple Solutions, and Number of iterations 13 ZAS | 10/21/2022 |
Grover's Search Algorithm 𝛃 𝛂 Ψ = 1 𝑁 𝑥=0 𝑁−1 |x⟩ , 𝛂 = 1 𝑁 − 1 𝑥≠𝑤 |x⟩ 𝛃 = 𝒘 • Generate a rotation in a two-dimensional plane • A reflection around the axis 𝛂 • A reflection around the axis Ψ • θ is the angle between 𝛂 and Ψ Grover’s Algorithm: Geometric Interpretation Ψ 𝜃 U Ψ 𝜃 𝐷𝑈 Ψ 2𝜃 14 ZAS | 10/21/2022 |
Grover's Search Algorithm 𝛃 𝛂 Grover’s Algorithm: Geometric Interpretation Ψ 𝜃 U Ψ 𝜃 𝐷𝑈 Ψ 2𝜃 15 ZAS | 10/21/2022 | 00 01 10 11 𝜳 00 01 10 11 𝑼 𝜳 00 01 10 11 𝐷𝑈 Ψ
Grover's Search Algorithm • One solution • |Ψ⟩ = 𝑁−1 𝑁 |𝛂⟩ + 1 𝑁 𝛃 • Ψ = cos 𝜃 |𝛂⟩ + sin 𝜃 𝛃 • Number of iterations 𝜋 4 𝑵 Grover’s Algorithm: Geometric Interpretation Ψ 𝛃 𝛂 𝑈 Ψ 𝜃 𝐷𝑈 Ψ 2𝜃 16 ZAS | 10/21/2022 | 𝜃
Grover's Search Algorithm • Multiple Solutions |Ψ⟩ = 𝑁 − 𝑀 𝑁 |𝛂⟩ + 𝑀 𝑁 𝛃 Ψ = cos 𝜃 |𝛂⟩ + sin 𝜃 𝛃 •  Assume 𝐺 = 𝐷𝑈 • The first application of 𝐺 on the state 𝜓 𝐺 Ψ = cos 3𝜃 |𝛂⟩ + sin 3𝜃 𝛃 • The 𝑡th application of 𝐺 or the state |𝜓⟩, gives: • 𝐺t Ψ = cos(2𝑡 + 1)𝜃 |𝛂⟩ + sin(2𝑡 + 1)𝜃 𝛃 • Number of iterations 𝜋 4 𝑁 𝑀 Grover’s Algorithm: Geometric Interpretation Ψ 𝜃 𝛃 𝛂 𝑈 Ψ 𝜃 𝐷𝑈 Ψ 2𝜃 17 ZAS | 10/21/2022 |
Grover's Search Algorithm • Number of iterations • To maximize the probability of obtaining 𝛃 • Assume that θ= 1 𝑁 • sin((2t + 1)θ) ≈ 1 • (2t+ 1)θ ≈ 𝜋 𝟐 • 2t+1= 𝜋 𝟐θ • t= 𝜋 4θ - 1 𝟐 • t= 𝜋 4 𝑵 − 1 𝟐 = 𝜋 4 𝑵 Grover’s Algorithm: Geometric Interpretation Ψ 𝜃 𝛃 𝛂 𝑈 Ψ 𝜃 𝐷𝑈 Ψ 2𝜃 18 ZAS | 10/21/2022 |
Grover's Search Algorithm 3- Required Gates: Hadamard, X, Z , and CZ Gates 19 ZAS | 10/21/2022 |
Grover's Search Algorithm Grover’s Algorithm: Hadamard Gate 20 ZAS | 10/21/2022 | Hadamard Gate Create an equal superposition of the two basis states Matrix Symbol IBM Quantum Symbol Input Output 𝟏 𝟐 𝟏 𝟏 𝟏 −𝟏 H H ∣ 0⟩ 1 2 (∣ 0⟩ +∣ 1⟩ H ∣ 1⟩ 1 2 (∣ 0⟩ −∣ 1⟩
Grover's Search Algorithm Grover’s Algorithm: Z Gate 21 ZAS | 10/21/2022 | Z Gate Make π-rotation for quantum bit around the Z-axis Matrix Symbol IBM Quantum Symbol Input Output Z= 1 0 0 −1 Z Z ∣ 0⟩ ∣ 0⟩ Z ∣ 1⟩ −∣ 1⟩
Grover's Search Algorithm Grover’s Algorithm: X Gate 22 ZAS | 10/21/2022 | X Gate Change quantum bit from state to another (Not gate) Matrix Symbol IBM Quantum Symbol Input Output 0 1 1 0 X X ∣ 0⟩ ∣ 1⟩ X ∣ 1⟩ ∣ 0⟩
Grover's Search Algorithm Grover’s Algorithm: Identity Gate 23 ZAS | 10/21/2022 | Identity Gate Mapping each state to itself. Matrix Symbol IBM Quantum Symbol Input Output 1 0 0 1 𝑰 𝑰 ∣ 0⟩ ∣ 0⟩ 𝑰 ∣ 1⟩ ∣ 1⟩
Grover's Search Algorithm Grover’s Algorithm: Controlled-Z Gate 24 ZAS | 10/21/2022 | Controlled-Z (CZ) Gate leaves the control qubit unchanged and performs a Z gate on the target qubit when the control qubit is in state |1⟩ Matrix Symbol IBM Quantum Symbol Input Output 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 −1 CZ CZ ∣ 00⟩ ∣ 00⟩ CZ∣ 01⟩ ∣ 01⟩ CZ∣ 10⟩ ∣ 10⟩ CZ∣ 11⟩ -∣ 11⟩
Grover's Search Algorithm 4- Implementation of 2-qubits Grover’s Algorithm Using Qiskit 25 ZAS | 10/21/2022 |
Grover's Search Algorithm Grover’s Algorithm: Implementation of 2-qubits 26 ZAS | 10/21/2022 | Number of items=N=4 Ψ = |00⟩ + |01⟩ + 10⟩ + |11⟩ Target item= w = 1 |01⟩ Number of qubits=n 2 Number of iterations=t 𝜋 4 𝑵= 𝜋 4 𝟒=1
Grover's Search Algorithm The procedure of Grover’s algorithm is as follows: Creating a uniform superposition Apply the oracle function (𝑈) Apply amplitude amplification ( Grover diffuser operator) (D) Repeat step U and D 𝜋 4 𝑵 iterations Apply the measurement 2 3 4 5 Grover’s Algorithm: Steps 27 ZAS | 10/21/2022 |
Grover's Search Algorithm Grover’s Algorithm: Implementation of 2-qubits 28 ZAS | 10/21/2022 | Step1 : Creating a uniform superposition by applying hadamard gate |Ψ⟩ = 𝐻⊕𝒏 𝐻⊕𝟐 = 𝐻 ⊕ 𝐻 𝟏 𝟐 𝟏 𝟏 𝟏 −𝟏 ⊕ 𝟏 𝟐 𝟏 𝟏 𝟏 −𝟏 = 𝟏 𝟏 𝟏 𝟏 −𝟏 𝟏 𝟏 𝟏 𝟏 −𝟏 𝟏 𝟏 𝟏 𝟏 −𝟏 −𝟏 𝟏 𝟏 𝟏 −𝟏 = 𝟏 𝟐 𝟏 𝟏 𝟏 𝟏 𝟏 −𝟏 𝟏 −𝟏 𝟏 𝟏 −𝟏 −𝟏 𝟏 −𝟏 −𝟏 𝟏
Grover's Search Algorithm Grover’s Algorithm: Implementation of 2-qubits 29 ZAS | 10/21/2022 | Step1 : Creating a uniform superposition by applying hadamard gate = 𝟏 𝟐 𝟏 𝟏 𝟏 𝟏 𝟏 −𝟏 𝟏 −𝟏 𝟏 𝟏 −𝟏 −𝟏 𝟏 −𝟏 −𝟏 𝟏 1 0 0 0 = 𝟏 𝟐 1 1 1 1
Grover's Search Algorithm The procedure of Grover’s algorithm is as follows: Creating a uniform superposition Apply the oracle function (𝑈) Apply amplitude amplification ( Grover diffuser operator) (D) Repeat step U and D 𝜋 4 𝑵 iterations Apply the measurement 2 3 4 5 Grover’s Algorithm: Steps 30 ZAS | 10/21/2022 |
Grover's Search Algorithm Grover’s Algorithm: Implementation of 2-qubits 31 ZAS | 10/21/2022 | Step2 :Apply the oracle function (𝑈) for item |01⟩ by applying CZ and X gates 𝑰 ⊗ 𝐗 𝑪𝒁 𝑰 ⊗ 𝐗 1 0 0 1 ⊗ 0 1 1 0 𝟏 𝟎 𝟎 𝟎 𝟎 𝟏 𝟎 𝟎 𝟎 𝟎 𝟏 𝟎 𝟎 𝟎 𝟎 −𝟏 1 0 0 1 ⊗ 0 1 1 0 = 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 −1 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0
Grover's Search Algorithm Grover’s Algorithm: Implementation of 2-qubits 32 ZAS | 10/21/2022 | Step2 :Apply the oracle function (𝑈) for item |01⟩ by applying CZ and X gates 𝑰 ⊗ 𝐗 𝑪𝒁 𝑰 ⊗ 𝐗 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 −1 0 0 𝑈= 1 0 0 0 0 −1 0 0 0 0 1 0 0 0 0 1
Grover's Search Algorithm The procedure of Grover’s algorithm is as follows: Creating a uniform superposition Apply the oracle function (𝑈) Apply amplitude amplification ( Grover diffuser operator) (D) Repeat step U and D 𝜋 4 𝑵 iterations Apply the measurement 2 3 4 5 Grover’s Algorithm: Steps 33 ZAS | 10/21/2022 |
Grover's Search Algorithm Grover’s Algorithm: Implementation of 2-qubits 34 ZAS | 10/21/2022 | Step3 :Apply Grover diffuser operator (D) by applying H , Z and CZ gates D= 2|Ψ⟩⟨Ψ| − 𝐼 = ((2|0⟩n⟨0|n−𝑰)) = ((2|0⟩2⟨0|2 − 𝑰) 2|0⟩2⟨0|2 − 𝑰=2 1 0 0 0 1 0 0 0 − 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 = 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 − 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 = 1 0 0 0 0 −1 0 0 0 0 −1 0 0 0 0 −1
Grover's Search Algorithm Grover’s Algorithm: Implementation of 2-qubits 35 ZAS | 10/21/2022 | Step3 :Apply Grover diffuser operator (D) by applying H , Z and CZ gates D= 2|Ψ⟩⟨Ψ| − 𝐼 (𝒁 ⊕ 𝒁) CZ=2|0⟩2⟨0|2 − 𝑰 𝟏 𝟏 𝟏 −𝟏 ⊕ 𝟏 𝟏 𝟏 −𝟏 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 −1 = 1 0 0 0 0 −1 0 0 0 0 −1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 −1
Grover's Search Algorithm Grover’s Algorithm: Implementation of 2-qubits 36 ZAS | 10/21/2022 | Step3 :Apply Grover diffuser operator (D) by applying H , Z and CZ gates D= 2|Ψ⟩⟨Ψ| − 𝐼 (𝒁 ⊕ 𝒁) CZ=2|0⟩2⟨0|2 − 𝑰 = 1 0 0 0 0 −1 0 0 0 0 −1 0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 −1 = 1 0 0 0 0 −1 0 0 0 0 −1 0 0 0 0 −1
Grover's Search Algorithm Grover’s Algorithm: Implementation of 2-qubits 37 ZAS | 10/21/2022 | Step3 :Apply Grover diffuser operator (D) by applying H , Z and CZ gates D= 2|Ψ⟩⟨Ψ| − 𝐼 = 𝑯⊗𝒏((2|Ψ⟩n⟨Ψ|n − 𝑰) 𝑯⊗𝒏 Assume that |Ψ⟩=𝑯⊗𝒏|0⟩n ⟨Ψ|=⟨0|n 𝑯⊗𝑛 † 𝑯 †=𝑯 D= 2|Ψ⟩⟨Ψ| − 𝐼 =2𝑯⊗𝒏|0⟩n ⟨0|n ( 𝑯⊗𝑛 † −𝐼 =2𝑯⊗𝒏|0⟩n ⟨0|n𝑯⊗𝒏 − 𝑯⊗𝒏𝐼𝑯⊗𝒏 =𝑯⊗𝒏 (2|0⟩n ⟨0|n − 𝐼) 𝑯⊗𝒏
Grover's Search Algorithm 5- Circuit of 2-qubits Grover’s Algorithm: with IBM quantum Composer 38 ZAS | 10/21/2022 |
Grover's Search Algorithm Grover’s Algorithm: Circuit diagram of 2-qubits 39 ZAS | 10/21/2022 | 1- Creating a uniform superposition 2- Apply the oracle function (𝑈) 3- Apply amplitude amplification (D) 4- Repeat U and D 𝝅 𝟒 𝑵 iterations 5- Apply the measurement • Circuit diagram of 2-qubits for oracle item 𝟎𝟏 = 𝟏
Grover's Search Algorithm Grover’s Algorithm: Circuit diagram of 2-qubits 40 ZAS | 10/21/2022 | Grover’s algorithm of 2-qubits for oracle item 𝟎𝟏 = 𝟏 Remember that Ψ = 𝟏 𝟐 1 1 1 1 𝑈= 1 0 0 0 0 −1 0 0 0 0 1 0 0 0 0 1 =𝑯⊗𝟐 ((2|0⟩2⟨0|2 − 𝑰) 𝑯⊗𝟐 𝑈|Ψ⟩ Ψ = 𝟏 𝟐 1 1 1 1 = 1 2 (|00⟩ + |01⟩ + 10⟩ + |11⟩) 𝑈|Ψ⟩= 1 0 0 0 0 −1 0 0 0 0 1 0 0 0 0 1 𝟏 𝟐 1 1 1 1 = 𝟏 𝟐 1 −1 1 1
Grover's Search Algorithm Grover’s Algorithm: Circuit diagram of 2-qubits 41 ZAS | 10/21/2022 | Grover’s algorithm of 2-qubits for oracle item 𝟎𝟏 = 𝟏 Remember that 𝑈|Ψ⟩= 𝟏 𝟐 1 −1 1 1 𝐻⊕𝟐 = 𝟏 𝟐 𝟏 𝟏 𝟏 𝟏 𝟏 −𝟏 𝟏 −𝟏 𝟏 𝟏 −𝟏 −𝟏 𝟏 −𝟏 −𝟏 𝟏 =𝑯⊗𝟐((2|0⟩2⟨0|2 − 𝑰) 𝑯⊗𝟐 𝑼|Ψ⟩ = 𝟏 𝟐 𝟏 𝟏 𝟏 𝟏 𝟏 −𝟏 𝟏 −𝟏 𝟏 𝟏 −𝟏 −𝟏 𝟏 −𝟏 −𝟏 𝟏 1 0 0 0 0 −1 0 0 0 0 −1 0 0 0 0 −1 𝟏 𝟐 𝟏 𝟏 𝟏 𝟏 𝟏 −𝟏 𝟏 −𝟏 𝟏 𝟏 −𝟏 −𝟏 𝟏 −𝟏 −𝟏 𝟏 𝟏 𝟐 1 −1 1 1 = 𝟏 𝟐 𝟏 𝟏 𝟏 𝟏 𝟏 −𝟏 𝟏 −𝟏 𝟏 𝟏 −𝟏 −𝟏 𝟏 −𝟏 −𝟏 𝟏 𝟏 𝟐 1 −1 1 1 = 𝟏 𝟒 2 2 −2 2 = 𝟏 𝟐 1 1 −1 1
Grover's Search Algorithm Grover’s Algorithm: Circuit diagram of 2-qubits 42 ZAS | 10/21/2022 | Grover’s algorithm of 2-qubits for oracle item 𝟎𝟏 = 𝟏 Remember that 2|0⟩2⟨0|2 − 𝑰 = 1 0 0 0 0 −1 0 0 0 0 −1 0 0 0 0 −1 𝑯⊗𝟐 𝑈 Ψ = 1 1 −1 1 =𝑯⊗𝟐 (2|0⟩2⟨0|2 − 𝑰) 𝑯⊗𝟐 𝑈|Ψ⟩ = 𝟏 𝟒 𝟏 𝟏 𝟏 𝟏 𝟏 −𝟏 𝟏 −𝟏 𝟏 𝟏 −𝟏 −𝟏 𝟏 −𝟏 −𝟏 𝟏 1 0 0 0 0 −1 0 0 0 0 −1 0 0 0 0 −1 1 1 −1 1 = 1 −1 1 −1
Grover's Search Algorithm Grover’s Algorithm: Circuit diagram of 2-qubits 43 ZAS | 10/21/2022 | Grover’s algorithm of 2-qubits for oracle item 𝟎𝟏 = 𝟏 Remember that 𝐻⊕𝟐 = 𝟏 𝟐 𝟏 𝟏 𝟏 𝟏 𝟏 −𝟏 𝟏 −𝟏 𝟏 𝟏 −𝟏 −𝟏 𝟏 −𝟏 −𝟏 𝟏 (2|0⟩2⟨0|2 − 𝑰) 𝑯⊗𝟐 𝑈|Ψ⟩ = 1 −1 1 −1 =𝑯⊗𝟐 (2|0⟩2⟨0|2 − 𝑰) 𝑯⊗𝟐 𝑈|Ψ⟩ = 𝟏 𝟒 𝟏 𝟏 𝟏 𝟏 𝟏 −𝟏 𝟏 −𝟏 𝟏 𝟏 −𝟏 −𝟏 𝟏 −𝟏 −𝟏 𝟏 1 −1 1 −1 = 𝟏 𝟒 0 4 0 0 = 0 1 0 0 = 𝟎𝟏 =|𝐰⟩
Grover's Search Algorithm • Grover, Lov K. "A fast quantum mechanical algorithm for database search." Proceedings of the twenty- eighth annual ACM symposium on Theory of computing. 1996. • https://qiskit.org/textbook/ch-algorithms/grover.html • Introduction to Quantum Computing: From a Layperson to a Programmer in 30 Steps: Wong, Hiu Yung: 9783030983383: Amazon.com: Books • Learn Quantum Computing with Python and IBM Quantum Experience: A hands-on introduction to quantum computing and writing your own quantum programs with Python: Loredo, Robert: 9781838981006: Amazon.com: Books References 44 ZAS | 10/21/2022 |
Grover's Search Algorithm Let me know your comments, please contact me via. zeinababohashima20@gmail.com 45 ZAS | 10/21/2022 |
Grover's Search Algorithm Thanks Any Questions? 46 ZAS | 10/21/2022 |