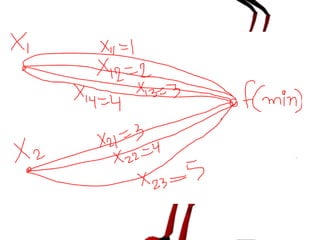
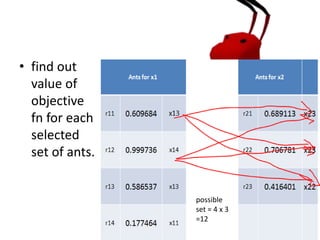
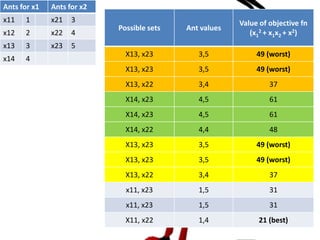
This document describes an example of using ant colony optimization to minimize the objective function f(x1, x2) = x1^2 + x1x2 + x2, where x1 can take on values 1, 2, 3, 4 and x2 can take values 3, 4, 5. It initializes pheromone values and assigns ants to different variable values. Over multiple iterations, it calculates probabilities, selects variable values, evaluates objective functions, and updates pheromone values by increasing them for the best solutions found so far.

1. Ant Colony Optimization
Numerical Example
By :- Harish Kant Soni
Roll No:- 12CE31004
IIT Kharagpur

2. Problem
• min (x1
2 + x1x2 + x2)
• x1 = [1,2,3,4]
• x2= [3,4,5]

3. It’s better to assume same of no
ants as no of values.
So we take 4 ants for x1
and 3 ants for x2

4. • Each ant is assigned a
discrete value.
• x1j , j = 1,2,3,4
• x2k , k = 1,2,3
Ants for x1 Ants for x2
x11 1 x21 3
x12 2 x22 4
x13 3 x23 5
x14 4

6. • Assume equal
pheromone for
each path = 1

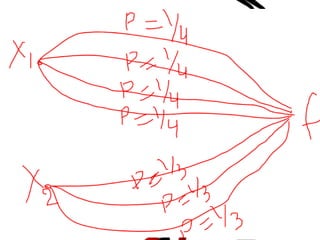
7. Iteration=1
• for any ant k the probability
of selecting it’s path is given
by
• P1j = τ1j
τ1 𝑚
4
𝑚=1
= ¼,
where j = [1,2,3,4]
• P2k = τ2k
τ1 𝑚
3
𝑚=1
= 1/3
where k = [3,4,5]

9. • set roulette wheel
using cdf for each
ant.
Ants for r1 Ants for r2
x11 (0,0.25) x21 (0,0.33)
x12 (0.25, 0.50) x22 (0.33,0.67)
x13 (0.50, 0.75) x23 (0.67, 1)
x14 (0.75,1)

10. • generate random
numbers for each ant
and find out which ant
is selected using
cdf(roulette wheel ).
Ants for x1 Ants for x2
r11 0.609684 x13 r21 0.689113 x23
r12 0.999736 x14 r22 0.706781 x23
r13 0.586537 x13 r23 0.416401 x22
r14 0.177464 x11

11. • find out
value of
objective
fn for each
selected
set of ants.
possible
set = 4 x 3
=12

12. Possible sets Ant values
Value of objective fn
(x1
2 + x1x2 + x2)
X13, x23 3,5 49 (worst)
X13, x23 3,5 49 (worst)
X13, x22 3,4 37
X14, x23 4,5 61
X14, x23 4,5 61
X14, x22 4,4 48
X13, x23 3,5 49 (worst)
X13, x23 3,5 49 (worst)
X13, x22 3,4 37
x11, x23 1,5 31
x11, x23 1,5 31
X11, x22 1,4 21 (best)
Ants for x1 Ants for x2
x11 1 x21 3
x12 2 x22 4
x13 3 x23 5
x14 4

13. Iteration 2
Local pheromone update is an
extension of what we are doing so we
will not consider local updatation.
Q/Lk
Q= constant

14. Iteration 2
• assume ρ = 0.4 and Q = 2
• Update pheromone for each ant
• Increase pheromone for x11 and x22 as
they are giving best solution.
• Evaporate pheromone for other paths
• Δτ =Q best/worst
• best = 21 (only 1 time so z = 1)
Updated Pheromone
Ants for x1 Ants for x2
x11 1 (1-0.4)x1 + 2x21/49 = 1.457 x21 3 (1-0.4)x1 = 0.6
x12 2 (1-0.4)x1 = 0.6 x22 4 (1-0.4)x1 + 2x21/49 = 1.457
x13 3 (1-0.4)x1 = 0.6 x23 5 (1-0.4)x1 = 0.6
x14 4 (1-0.4)x1 = 0.6

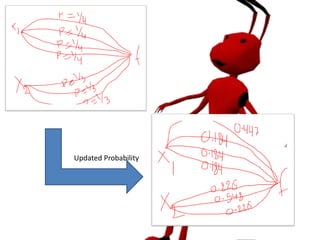
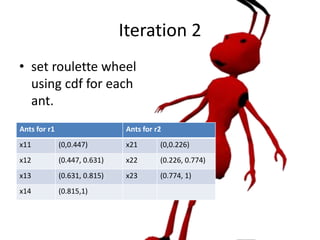
15. Iteration 2
• Update probability
• P1j = τ1j
τ1 𝑚
4
𝑚=1
= ?,
where j = [1,2,3,4]
• P2k = τ2k
τ1 𝑚
3
𝑚=1
= ?
where k = [3,4,5]
Ants for x1 Ants for x2
x11 0.447 x21 0.226
x12 0.184 x22 0.548
x13 0.184 x23 0.226
x14 0.184

16. Updated Probability

17. Iteration 2
• set roulette wheel
using cdf for each
ant.
Ants for r1 Ants for r2
x11 (0,0.447) x21 (0,0.226)
x12 (0.447, 0.631) x22 (0.226, 0.774)
x13 (0.631, 0.815) x23 (0.774, 1)
x14 (0.815,1)

18. Iteration 2
• generate random
numbers for each ant
and find out which ant
is selected using
cdf(roulette wheel ).
Ants for x1 Ants for x2
r11 0.2356 x11 r21 0.386493 x22
r12 0.42656 x11 r22 0.526781 x22
r13 0.58687 x12 r23 0.795401 x23
r14 0.7864 x13
x11 and x22 were
having higher
probability as they
were best solutions
so they are selected
twice

19. Iteration 2
• Evaluate objective
function value and
repeat the procedure
till convergence