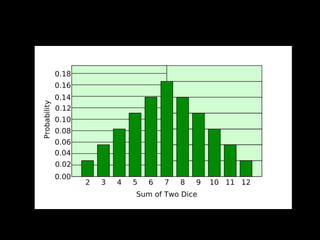
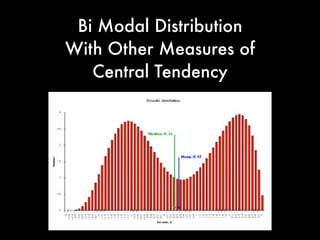
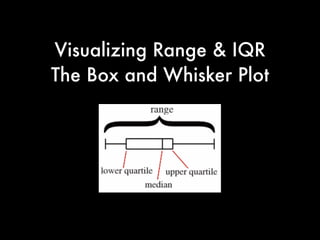
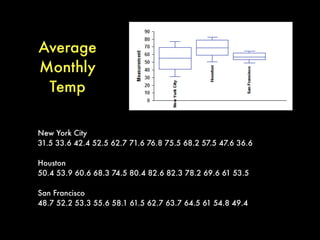
The document provides a comprehensive introduction to basic probability and statistics targeted at lawyers, covering concepts such as probability measures, statistical independence, and measures of central tendency. It includes examples involving dice, coins, and playing cards to illustrate these concepts. Additionally, it touches on the importance of understanding distributions and variability, highlighting tools like box plots and interquartile ranges.

1. Quantitative
Methods
for
Lawyers
Probability &
Basic Statistics (Part 1)
Class #6
@ computational
computationallegalstudies.com
professor daniel martin katz danielmartinkatz.com
lexpredict.com slideshare.net/DanielKatz

2. Basic Probability

3. Probability is a measure of how likely it is for an event to
happen.
We name a probability with a number from 0 to 1.
If an event is certain to happen, then the probability of the
event is 1 and certain not to happen, then the probability of
the event is 0.
Coin Flip with a Fair Coin
P(H) = .5
P(T) = .5
Basic Probability

4. If it is uncertain whether or not an event will happen, then
its probability is some fraction between 0 and 1 (or a
fraction converted to a decimal number).
0 1
Certain not
to happen
Equally likely to
happen or not to happen Certain to
happen
0%
50 %
Chance
100%

5. Basic Probability
Die
Dice

6. Basic Probability
Die Assuming the Die is Fair
Probability that
(1) You will Roll a 5?
(2) Probability you will
Roll a 5 if 5 has Just
Been Rolled

7. Basic Probability
Die
Assuming the Die
is Fair ...
This is a Random
Event

8. Basic Probability
http://www.math.csusb.edu/faculty/stanton/m262/intro_prob_models/
intro_prob_models.html

9. Basic Probability2
3
4
5
6
7
8
9
10
11
12 Please Calculate the Frequency
http://ccl.northwestern.edu/netlogo/models/DiceStalagmite

10. Basic Probability
2 1 1/36
3 2 2/36
4 3 3/36
5 4 4/36
6 5 5/36
7 6 6/36
8 5 5/36
9 4 4/36
10 3 3/36
11 2 2/36
12 1 1/36

11. Basic Probability
Two Dice

12. When two events are statistically independent, it means
that knowing whether one of them occurs makes it
neither more probable nor less probable that the other
occurs.
the occurrence of one event occurs does not affect the
outcome of the occurrence of the other event. Similarly,
when we assert that two random variables are
independent, we intuitively mean that knowing
something about the value of one of them does not
yield any information about the value of the other.
Statistical Independence

13. Example: The number appearing on the upward face of
a die the first time it is thrown and that appearing on the
same die the second time, are independent. e.g. the
event of getting a "1" when a die is thrown and the
event of getting a "1" the second time it is thrown are
independent.
Statistical Independence

14. Basic Probability:
Coins
What is the Prob of Heads v. Tails?
What is the Prob of TT?
What is the Prob of HHH,?
What is the Prob of HTT?

15. This is
Binomial

16. Basic Probability
With A Deck of Cards

17. Note: the Probability Changes
when Each Card is Drawn
Poker / Blackjack

18. Basic Probability
A Deck of Cards

19. Basic
Probability
A Deck of Cards
1. A red card
2. A spade
3. Not a spade
4. An ace
5. Not an ace
6. The ace of spades
7. A picture card
8. A number card or ‘not a picture card‘
9. A card that is either a heart or a club
10. A 4 or 5 but not a spade
11. An even numbered card

20. 1. A red card 26/52 ½
2. A spade 13/52 ¼
3. Not a spade 39/52 ¾
4. An ace 4/52 1/13
5. Not an ace 48/52 12/13
6. The ace of spades 1/52
7. A picture card 12/52 3/13
8. A number card or ‘not a picture card’ 40/52 10/13
9. A card that is either a heart or a club 26/52 ½
10. A 4 or 5 but not a spade 6/52 3/26
11. An even numbered card 20/52 5/13

21. Life
Expectancy
Calculator
http://www.msrs.state.mn.us/
info/Age_Cal.htmls

22. Quick Primer
on
Set Theory

23. Let's say that our universe contains the numbers
1, 2, 3, and 4.
Let A be the set containing the numbers 1 and 2; that is,
A = {1, 2}.
(Warning: The curly braces are the customary notation for
sets. Do not use parentheses or square brackets.)
Let B be the set containing the numbers
2 and 3; that is, B = {2, 3}. Then we
have the following relationships, with
pinkish shading marking the solution
"regions" in the Venn diagrams:

24. Let's say that our
universe contains the
numbers 1, 2, 3, and
4.
Let A be the set
c o n t a i n i n g t h e
numbers 1 and 2;
that is, A = {1, 2}.
Let B be the set
c o n t a i n i n g t h e
numbers 2 and 3;
that is, B = {2, 3}.

25. Plot the Probability Distribution
for Two Dice

27. If You Need
Additional Assistance

29. Probability: mathematical theory that describes
uncertainty
Statistics: series of techniques for describing and
extracting useful information from data
Probability Versus Statistics

30. The arithmetic mean (or average) is
the sum of a series dividing by how
many numbers you added together.

31. Sum of Series of Numbers
Total # of Numbers in the Series
_____________________________________________________________________________
Mean =

32. Lets Talk About Notation ...
x1, x2, x3 x4 .... xn
5, 7, 11, 13 ....
x bar
the Nth Term
Called

33. Lets Talk About Notation ...
x1, x2, x3 x4 .... xn
5, 7, 11, 13 ....
x bar
the Nth Term
Called

34. Calculating Measures of
Central Tendency
Series 1: 0, 0, 0, 0, 50, 50, 100, 100, 100, 100
Series 2: 10, 20, 30, 40, 50, 50, 60, 70, 80, 90, 100
Series 3: 55, 60, 75, 77, 80, 83, 83, 83, 88, 91, 93
Please Calculate the arithmetic mean

35. Measures of Central Tendency
The number that occurs most frequently is
the mode.
When numbers are arranged in numerical
order, the middle one is the median.

36. Measures of Central Tendency
Series 1: 0, 0, 0, 0, 50, 50, 100, 100, 100, 100
Series 2: 10, 20, 30, 40, 50, 50, 60, 70, 80, 90, 100
Series 3: 55, 60, 75, 77, 80, 83, 83, 83, 88, 91, 93
Please Calculate the Median & Mode

37. Bi Modal Distribution

38. Bi Modal Distribution
With Other Measures of
Central Tendency

39. Range
Range is the difference between the largest
and smallest values in a set of values.
For example, consider the following numbers:
1, 2, 4, 7, 8, 9, 11.
For this set of numbers, the range would be
11 - 1 or 10.

40. Range &
Interquartile Range
The interquartile range (IQR) is a measure of
variability, based on dividing a data set into
quartiles
The interquartile range is equal to Q3 minus Q1

41. Range &
Interquartile Range
The interquartile range (IQR) is a measure of
variability, based on dividing a data set into
quartiles
The interquartile range is equal to Q3 minus Q1
Example:
0, 10, 20, 30, 40, 50, 50, 60, 70, 80, 90, 100

42. Visualizing Range & IQR
The Box and Whisker Plot

43. New York City
31.5 33.6 42.4 52.5 62.7 71.6 76.8 75.5 68.2 57.5 47.6 36.6
Houston
50.4 53.9 60.6 68.3 74.5 80.4 82.6 82.3 78.2 69.6 61 53.5
San Francisco
48.7 52.2 53.3 55.6 58.1 61.5 62.7 63.7 64.5 61 54.8 49.4
Average
Monthly
Temp

44. Visualizing Range & IQR
The Box and Whisker Plot
From
Google
Images

45. Daniel Martin Katz
@ computational
computationallegalstudies.com
lexpredict.com
danielmartinkatz.com
illinois tech - chicago kent college of law@