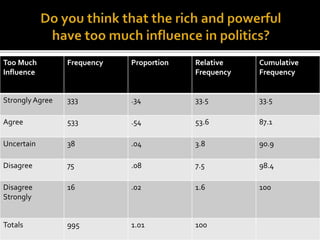
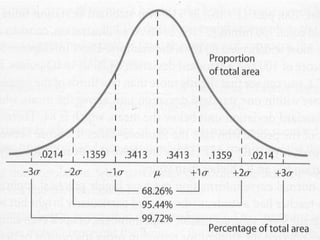
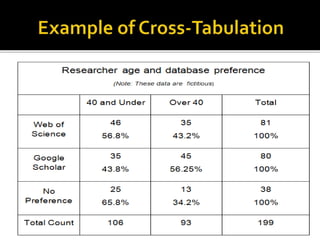
This document provides an overview of key concepts in statistics that will be covered in a geography, political science, or sociology course. It discusses research design, collecting and organizing data, different types of variables, descriptive statistics like measures of central tendency and dispersion, frequency distributions, and inferential statistics like correlation. The document is intended to prepare students to quantify, understand, present, and interpret their own research results using appropriate statistical techniques.

1. GEOG 420 / POL 420 / SOC 420
Fall 2019

4.  Once we have…
 Chosen research question
 Completed literature review
 Selected appropriate research design
▪ Survey; Experiment; Observation; Content Analysis
 Gathered data
 We can use statistics to quantify our results
for presentation and publication

5.  Understand your own and others’ results
 What do resulting numbers mean?
 Awareness of statistical results
 Remember “innumeracy?”

7.  Array of rows and columns that stores
observed values and variables
 Similar to Excel Spreadsheet
 What goes into these cells?
 Review different types of variables

8.  Nominal: Classification of observations into categories.
 Examples: Religious Faith, Race
 Ordinal: Observations can be compared by having more or less
of a particular attribute; uncertainty of equality.
 Example: Olympic Performance (Gold, Silver, Bronze medals)
 Interval: Intervals between values assigned to observations
have meaning and no meaningful zero point.
 Examples: Temperature; Dates
 Ratio: Interval variable properties with true zero point.
 Examples: Income;Years of Education

10.  Table showing number of observations and
each value of a variable
 “Lists” each variable’s possible values and
how often each occurs

11.  Raw Frequency
 Number of observations of a given variable
 Relative Frequency
 Number that transforms raw frequency into proportion or
percentage
▪ Proportion
▪ Percentage
 Cumulative Frequency
 Portion of total that is above or below a certain point

12. Too Much
Influence
Frequency Proportion Relative
Frequency
Cumulative
Frequency
StronglyAgree 333 .34 33.5 33.5
Agree 533 .54 53.6 87.1
Uncertain 38 .04 3.8 90.9
Disagree 75 .08 7.5 98.4
Disagree
Strongly
16 .02 1.6 100
Totals 995 1.01 100

14.  Describe characteristics or properties of a
set of numbers
 Two MainTypes:
 Measures of CentralTendency
 Measures of Dispersion

16. MEAN
 Locates the middle or
center of a distribution
 Most familiar measure of
central tendency;
“average”
 Add values of variable
and divide total by total
number of values
MEDIAN
 Divides distribution in half
 Odd-Numbered Set
 Even-Numbered Set
 Most appropriate with
ordinal-level data

17.  Commonly used when dealing with nominal or
categorical data
 Category with the greatest frequency of
observations
 If distribution has one mode = unimodal
 If distribution has two modes = bimodal
 If distribution has many modes = multimodal

19.  No variability (all scores have same value),
then variability = 0
 Measure will always be positive number
(cannot be “less than zero” variation)
 Greater variability of data, larger the measure

20.  Largest (maximum) value
of variable minus smallest
(minimum) value
INTERQUARTILE RANGE
 Divide observations into
four equal portions
 First batch contains 25% of
cases, 2nd would have 25%,
and so would the 3rd and 4th
grouping; division points
are called quartiles
 Finding range, but using 3rd
quartile (Q3) as maximum
and 1st quartile (Q1) as
minimum values
RANGE

21. INSTRUCTIONS
In groups, calculate the various
descriptive statistics
for each set of numerical data.

23.  Variance
 Standard Deviation

26.  Displays distribution of one variable for each
category of another variable
 Steps to Creating Cross-Tabs:
 #1: Record respondents’ answers to question
 #2: Create categories for table
 #3: Count number of respondents who fall into
each category
 #4: Convert tallies to frequencies;
add up row and column tables

29.  Statistical technique centered on
expressing relationship between two
quantitative variables with a linear equation
 Idea of “Best Fit Line”
 Correlation Coefficient (r)
 Coefficient of Determination (R2)