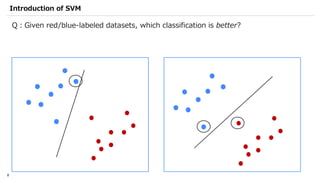
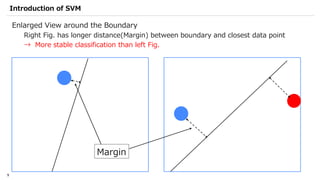
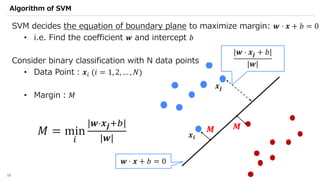
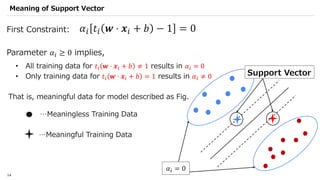
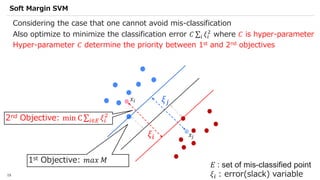
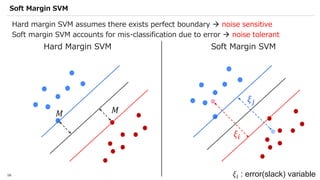
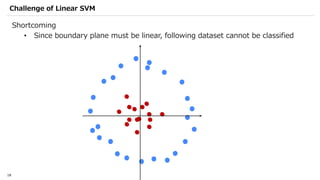
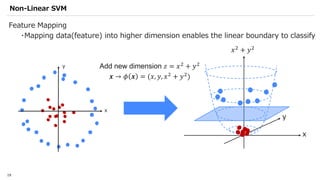
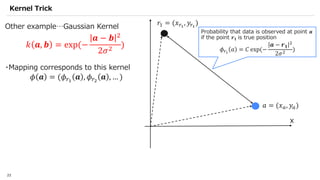
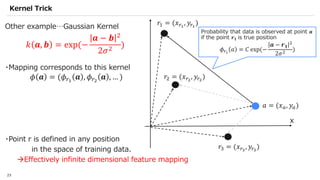
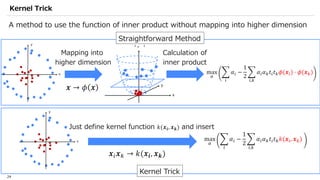
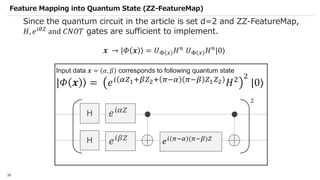
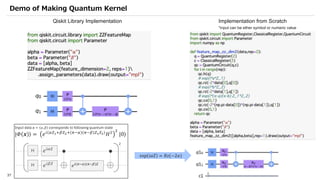
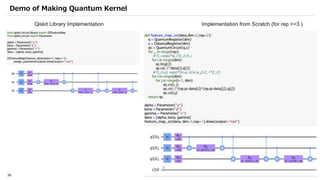
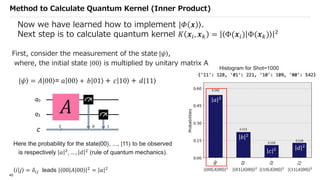
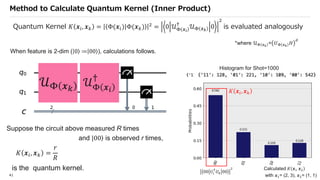
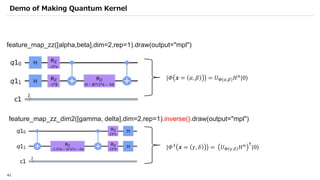
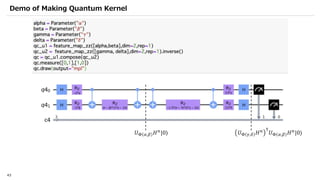
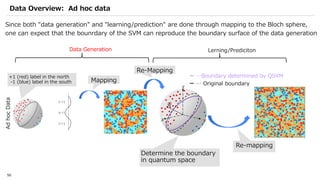
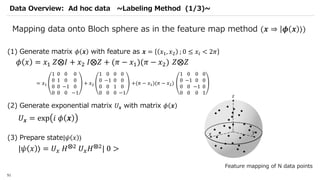
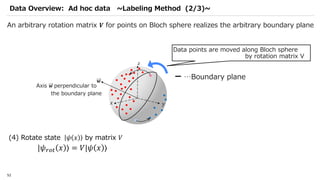
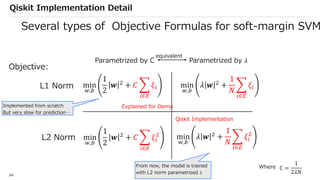
Yuma Nakamura is a data scientist at IBM Japan who specializes in quantum machine learning. He has degrees in chemistry and physics from Tsinghua University and Tohoku University. Previously he conducted research at Oak Ridge National Laboratory related to material simulation and quantum annealing. At IBM, his work involves machine learning and data analysis for healthcare clients. He currently chairs an internal study group on quantum machine learning and serves as a Qiskit Advocate, helping to translate Qiskit documentation and create educational content.