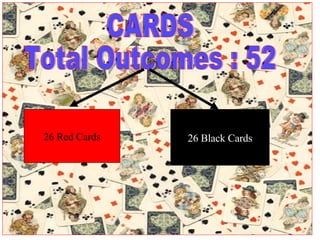
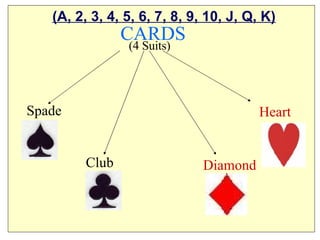
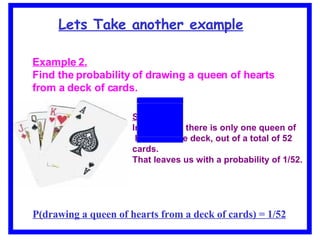
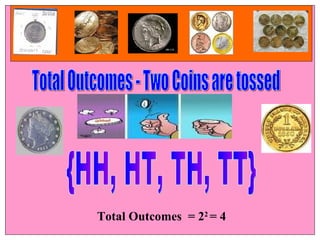
The document discusses the concept of probability, including defining it as a measure of likelihood between 0 and 1, and how to calculate probabilities using concepts like sample spaces, favorable outcomes, and total possible outcomes. It provides examples of calculating probabilities from experiments involving dice, cards, and coins. The document also outlines some applications of probability theory in areas like risk assessment, commodity markets, product reliability, and environmental regulation.

1. Probability Ms. Aarti Kulachi Hansraj Model School Class X

2. Objectives Given an experiment, define the probability of an event. Identify the outcomes of an experiment and represent them in a set S (outcome space). Identify events as subsets of the outcome space. Compute the probability of an event by computing the proportion of outcomes that result in the event's occurrence.

3. Objectives To compute the probability of the occurrence of an event . To construct a sample space for a probability. To compute the odds that an event will occur. To compute the empirical probability that an event will occur. Explain that the relative frequency of an event calculated from an experiment.

4. What Probability is??????…… Probability is the measure of how likely an event is. "the ratio of the number of favourable cases to the number of all the cases"

5. History of the concept Pierre de Fermat ( 1601 – 1665) People started to use the principles of probability many years ago. It is a well-known fact that the elements of probability were applied for census of population in the ancient countries such as China, India and Egypt. The same methods were used for estimation of the overall strength of enemy army. Blaise Pascal (1623-1662)

6. Laws of Probability a probability is a number between 0 and 1 the probability of an event or proposition and its complement must add up to 1 the joint probability of two events is the product of the probability of one of them and the probability of the second, conditional on the first.

7. For any Event E , 0 < P ( E ) < 1 P(E ) = Total Favourable Outcomes Total Possible Outcomes

8. For a Sure Event E , P(E) = 1 Example: Tossing a dart For example, Imagine throwing a dart at a square, and imagine that this square is the only thing in the universe. There is physically nowhere else for the dart to land. Then, the event that &quot;the dart hits the square&quot; is a sure event. No other alternative is imaginable.

9. For a Impossible Event E , P(E) = 0 Example: Tossing a die For example, Imagine Tossing a die. What is the probability of getting a number greater than 6? On a die there are a total of six outcomes {1,2,3,4,5,6} so we can’t have a number greater than 6. Such a event is called an impossible event.

10. Game of Dice

11. Sample Space - ( total outcomes ) when a die is thrown 1 2 3 6 5 4 Total Possible outcomes = 6 1 = 6

12. Lets take some examples Example : If a person rolls a dice, what is the probability of getting a five ? Sample Space 1 2 3 4 5 6 Favourable Outcomes 5 P ( Getting 5 ) = 1/6

13. Lets take another Example Example : If a person rolls a dice, what is the probability of getting a prime number? Sample Space Favourable Outcomes 2 P ( Getting a prime number ) = 3/6 3 5

14. Sample Space - ( total outcomes ) when 2 dice is thrown simultaneously Total Possible Outcomes = 6 2 = 36

15. Example :If a person rolls two dice, what is the probability of getting a five as the sum of the two dice? Sum Total of 5 3 2 1 4 2 3 4 1 , , P ( Getting a sum total of 5 ) = 4/36 Favourable Outcomes = 4 Total Outcomes = 36 Lets take another example

16. Game of Cards & Coins

17. CARDS Total Outcomes : 52 26 Red Cards 26 Black Cards

18. CARDS (4 Suits) Spade Club Diamond Heart (A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K)

19. Lets Take an example to understand the Game of Cards Example 1. Find the probability of drawing a diamond from a deck of cards. Solution. There are a total of 13 diamonds in the deck (A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K) and a total of 52 cards in the deck. That leaves us with a probability of: 13/52 = ¼ , ¼ makes sense, since there are a total of 4 suits in the deck of cards . P(drawing a diamond from a deck of cards) = 1/4

20. Lets Take another example Example 2. Find the probability of drawing a queen of hearts from a deck of cards. Solution. In this case, there is only one queen of hearts in the deck, out of a total of 52 cards. That leaves us with a probability of 1/52. P(drawing a queen of hearts from a deck of cards) = 1/52

21. Example 3. Find the probability of drawing a king of spade from a deck of cards. Solution. In this case, there is only one king of spade in the deck, out of a total of 52 cards. That leaves us with a probability of 1/52. P(drawing a king of spade from a deck of cards) = 1/52

22. Total Outcomes - A Coin is tossed Head Tail Total Outcomes = 2 1 = 2

23. Total Outcomes = 2 1 = 2 Example : What is the probability of getting a head when a coin is tossed? Total favourable outcomes = 1 Head Tail P(getting a head) = 1/2

24. Total Outcomes - Two Coins are tossed Total Outcomes = 2 2 = 4 {HH, HT, TH, TT}

25. {HH, HT, TH, TT} Sample Space = Example : Two coins are tossed simultaneously . What is the probability of getting at least one head? Total Favourable Outcomes = {HH} P ( Getting at most one head ) = 1/4

26. {HH, HT, TH, TT} Sample Space = Example : Two coins are tossed simultaneously . What is the probability of getting at most one head? Total Favourable Outcomes = {TT, HT, TH} P ( Getting at most one head ) = 3/4

27. Applications of probability theory to everyday life Two major applications of probability theory in everyday life are in risk assessment and in trade on commodity markets Governments typically apply probability methods in Environmental regulation where it is called “pathway analysis&quot;, significant application of probability theory in everyday life is reliabilty Many consumer products, such as automobiles and consumer electronics, utilize reliability theory in the design of the product in order to reduce the probability of failure.

28. Resources : Text Book NCERT Mathematics X R.D.Sharma Inernet : Google Search Yahoo search

29. THANK YOU!!