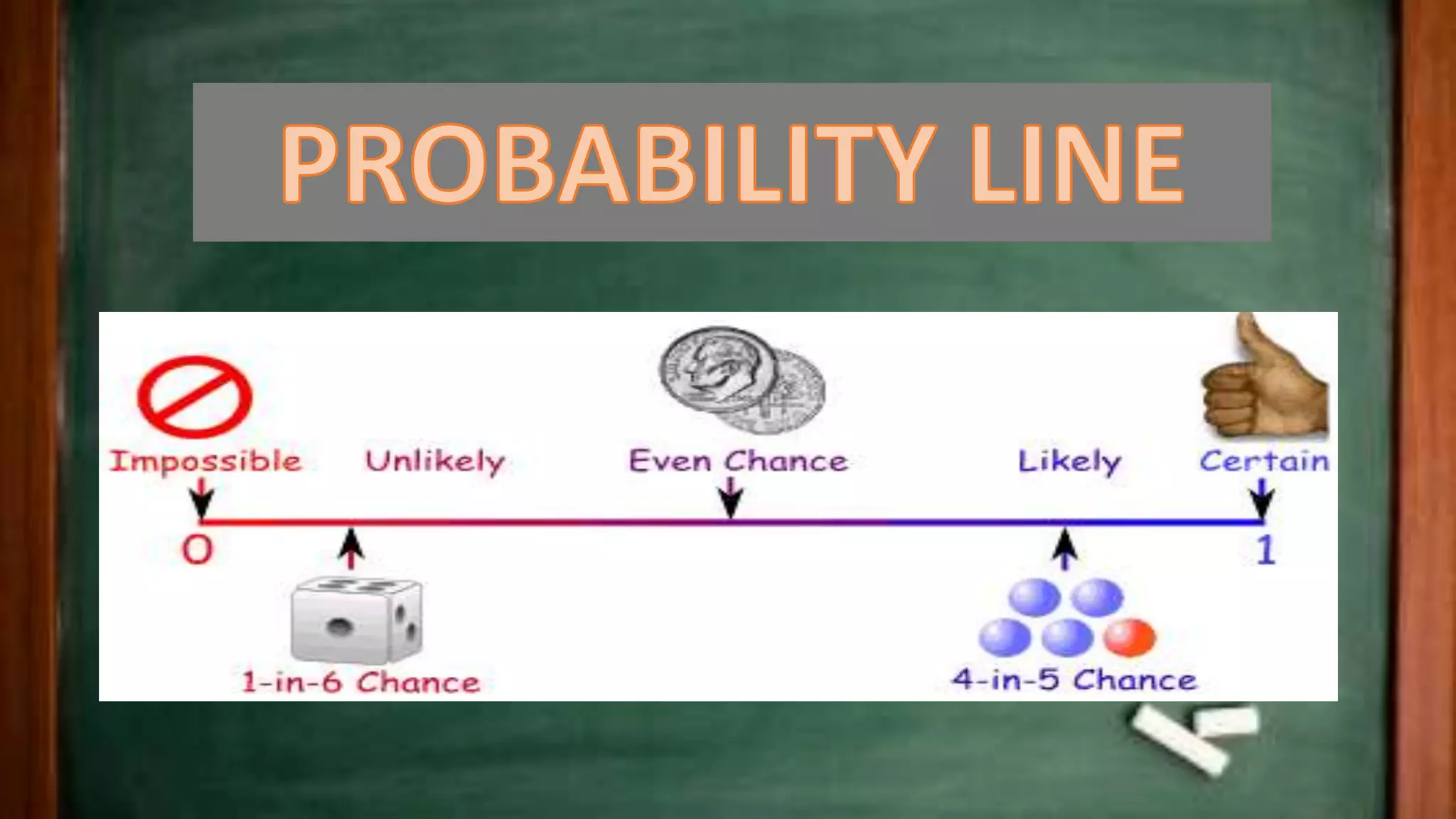
This document provides an overview of the history and key concepts of probability theory. It discusses how probability originated from games of chance and gambling. Some important early contributors are noted, including Cardano in the 16th century who wrote one of the first books on probability, and Galileo and Bernoulli who made quantitative advances. The definition of probability as a measure of likelihood is given. Key concepts explained include sample spaces, events, the addition and multiplication theorems, dependent and independent events, and applications of probability theory in fields like insurance, economics, and statistics.

2. HISTORY
 The theory has its origin in game of chances related to
gambling.
“Girolamo cardano (1501-76) ,an Italian mathematician , was
first man to wrote a book on subject entitled “Book on Games
of Chances” published after his death in 1663.
 Galileo (1564-1642), also an Italian mathematician was first
to attempt quantitative measure of probability.
 Jacques Bernoulli (1654-1705)was one who made extensive
study of subject for over 2 decades and his treatise on
probability is a major contribution to theory of probability.

3. DEFINITION-
Probability is measure of how likely something will
occur.
It is the ratio of desired outcomes to total outcomes.
( # desired/ # total)
A probability of an outcome is a number and has 2
properties-
1.The probability assigned to each outcome is non
negative
2.The sum of all the probabilities equals to 1.

5. Example –
Lets roll a dice once.
This is the sample space --- all possible outcomes.
S = { 1,2,3,4,5,6 }
Probability an
event will
occur
P (E) = NUMBER OF WAYS THAT E CAN OCCUR
E.g.. What is probability that you will roll an even number?
There are 3 ways to get an even number , rolling 2,4,6.
P(Even number) = 3/6 = 1 /2
( 6 in denominator because there are 6 different outcomes on dice)
NUMBER OF POSSIBILTITES

6. ADDITION THEOREM
It states that –
“ If two events A and B are mutually exclusive the probability of
occurrence of either A or B is the sum of individual probability of A and
B.
i.e. P(A U B ) = P(A) + P(B)
If A and B are not mutually exclusive events then –
P(A U B) = P(A) + P(B) – P( AB )
e.g. A single die is rolled ,probability of getting 2 or 5 = 1/6 + 1/6 = 1/ 3 .
e.g. A standard deck of card, a card is chosen probability that it’s a club
and king = 13/52 + 4/52 - 1/52 = 4/13.
A B

7. MULTIPLICATION THEOREM
It states that –
“If two events A and B are independent, the probability that they both will
occur is equal to the product of their individual probability.
i.e. P (AB) = P(A) * P(B)
If A and B are dependent events then –
P(AB) = P(A) * P(B/A)
P(B) * P(A/B)
where B/A is occurrence of B when A has already occurred and vice
versa for A/B.
e.g. A company wants to hire a person from good college probability is
1/6, good marks is 1/2 and indian manners and etiquettes
is1/10.probability that a man will posses all 3 = 1/6 * 1/2 * 1/10 = 0.008 .

8. NEED OF PROBABILITY -
 Probability models can be useful for making predictions.
 Concerned with constructions of econometric models , with managerial
decisions on planning.
 Provides a media of coping up with uncertainty.
 It is applied in the solution of social ,economic , political and business
problems.
 The insurance industry is emerged as the place which requires precise
knowledge about risk of loss.
 It is the foundation of statistical inference.

9. PRESENTED BY –
AVI VANI
M.A. Economics. 1st year.
School of Economics.