The document discusses techniques for indexing and querying graph data. It begins by categorizing graph queries as exact subgraph matching, similarity subgraph matching, or super graph matching. It then describes querying approaches for collection databases containing many small graphs versus large singular graphs. The document proceeds to summarize several graph indexing techniques including GraphGrep, gIndex, Grafil, C-tree, QuickSI, and others. It focuses on filtering techniques used to reduce the number of verification steps in subgraph matching queries over graph databases.

1. Graph Indexing Techniques
Seoul National University
IDB Lab.
Kisung Kim

2. Outline
• Category of graph queries
• Querying in collection DB
• Querying in large graphs
• References
2/50

3. Category of Graph Queries: Matching Type
• Exact subgraph matching
– Find graphs in DB which have all components of the query graph
• Similarity subgraph matching
– Find graphs in DB which have some components of the query graph
– Similarity measure is needed
• Super graph matching
– Find graphs in DB which are contained in the query graph
Query graph Exact subgraph Similarity
Subgraph
Query graph
3/50

4. Category of Graph Queries: Target DB
• Collection DB: large number of small graphs
– e.g. Chemical compounds
– Retrieval component
– IDs of graphs which contain matching parts
• Large graphs: small number of large graphs
– e.g. Social network, RDF graph
– Retrieval component
– All matching subgraphs
G1
G2
G3
G4
G7
G6
G5
Query graph
G1, G3, G5
Results: graph ID list
Querying Collection DB
Query graph
Results: matching subgraphs
Querying Large Graphs
4/50

5. Query Processing in Collection DB
• Processing flow
• Verification uses usual pair-wise subgraph isomorphism
algorithm
• Most of techniques focus on filtering techniques
– The cost of verification is high
– To reduce the number of verification execution
Query Filtering
Candidate
graph set
Verification
Answer
Graphs
5/50

6. Query Processing in Large Graphs
• Processing flow
• Focus on node indexing
– To reduce search space
– Use structural information of nodes
• Build subgraph by joining candidate nodes
– Join methods are not relatively researched
– Optimization using join ordering
Query
Index
search
Candidate
node sets
Building
subgraphs
Answer
subgraphs
6/50

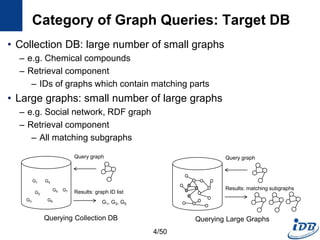
7. Graph Indexing Techniques
Target Database Query Type
GraphGrep
[Shasha et al., PODS’02]
Collection DB Exact Feature(Path) based index
gIndex
[Yan et al., SIGMOD’04]
Collection DB Exact Feature(Graph) based index
Grafil
[Yan et al., SIGMOD’05]
Collection DB Exact & Similarity Feature based similarity search
C-tree
[He and Singh, ICDE’06]
Collection DB Exact & Similarity Closure based index
QuickSI
[Shang et al., VLDB’08]
Collection DB Exact Verification algorithm
Tale
[Tian and Patel, ICDE’08]
Collection DB Exact & Similarity Similarity search using node index
GraphQL
[He and Singh, SIGMOD’08]
Large graphs Exact Node indexing
Spath
[Zhao and Han, VLDB’10]
Large graphs Exact
Node indexing using
neighborhood information
7/50

8. Outline
• Category of graph queries
• Querying in collection DB
• Querying in large graphs
• References
8/50

9. GraphGrep(1/2) [Shasha et al. PODS’02]
• First work adopts the filtering-and-verification framework
• Path-based index
– Fingerprint of database
– Enumerate the set of all paths(length <= L) of all graphs in DB
– For each path, the number of occurrences in each graphs are stored in
hash table
B
A
C
B
B
A
C
B
D
E
C
A B
B
C
Key g1 g2 g3
h(CA) 1 0 1
…
h(ABCB) 2 2 0
g1 g2 g3 Index
9/50

10. GraphGrep(2/2): Query Processing
• Filtering
– Make the fingerprint of query q
– Hash all paths (length <= L) of q
– Compare the fingerprint of the query with the fingerprint of database
– Discard a graph whose value in fingerprint is less than the value in query
fingerprint
• Verification
– Check subgraph isomorphism tests
Key g1 g2 g3
h(AB) 2 2 1
h(AC) 1 0 1
h(BAC) 2 0 1
B
A
C
B
B
A
C
B
D
E
C
A B
B
C
g1 g2 g3
Index
B
A C
AB:1
AC:1
BAC:1
Query
Candidates
= {g1, g3}
Verification
10/50

11. gIndex(1/6) [Yan et al., SIGMOD’04]
• Path-based approach has week points
– Path is too simple: structural information is lost
– There are too many paths: the set of paths in a graph database usually
is huge
• Solution
– Use graph structure instead of path as the basic index feature
c c c c
c c
c c
c c
c c
c c
c c
c c
c c
Sample Database
c
c c
c
c
c
Query
c c c
c c c
Paths in Query Graph
Cannot Filter Any
Graphs
In Database
11/50

12. gIndex(2/6): Frequent Fragment
• The number of graph structure is large
Index only frequent subgraphs
• support(g)
– The number of graphs in D (graph database), where g is a subgraph
• minSup
– Minimum support threshold
– Index a fragment, g only if support(g) ≥ minSup
• Size-increasing support
– Frequent fragments are increasing as the size of a fragment increases
– Low minSup for small fragments, high minSup for large fragment
12/50

13. gIndex(3/6): Frequent Fragment
A A
B
A A
B B
A A
B B
A
A
B B
A A
A B
A A B
A B B
B A B
A B A
A B
B
A
A A
B
A
B B
B A
B
A
B A
B
A
B B
A
A A
B B
A
A
A
B B
Size=1 Size=2 Size=3 Size=4
F=3
F=4
B B
F=3
F=3
F=3
F=2
F=2
F=2
F=1
F=1
F=1
F=1
F=2
F=1
F=1
13/50

14. gIndex(4/6): Discriminative Fragment
• Redundant fragment
– The indexed graphs by a fragment are also indexed by its subgraphs
– We don’t need to include redundant fragments
• Discriminative fragment
– Fragments which are not redundant
– 𝐷 𝑥 ≪ 𝑓∈𝐹⋀𝑓⊆𝑥 𝐷𝑓
A A
B
A A
B B
A A
B B
A A B
A B B
A B
B
A
Size=2 Size=3
Df1={g1, g2, g3}
Df2={g2, g3, g4}
Df3={g2, g3}=Df1∩Df2
f1
f2
f3
g1
g2
g3
A
A
B B
g4
14/50

15. a
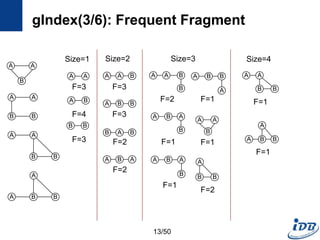
gIndex(5/6): gIndex Tree
• Use graph serialization method
– For fast graph isomorphism checking during index search
– DFS coding [Yan et al. ICDM’02]
– Translate a graph into a unique edge sequence
• gIndex Tree
– Prefix tree which consists of the edge sequences of discriminative fragments
– Record all size-n discriminative fragments in level n
– Black nodes  discriminative fragments
– Have ID lists: the ids of graphs containing fi
– White nodes  redundant fragments; for Apriori pruning
X
X
Z Y
b
a
ba
X
X
Z Y
b
ba
v0
v1
v2 v3
DFS Coding
<(v0,v1),(v1,v2),(v2,v0),(v1,v3)>
f1
f2
f3
e1
e2
e3
Level 0
Level 1
Level 2
…
gIndex Tree
15/50

16. gIndex(6/6): Searching
• Searching process
– Given a query q, enumerate all q’s fragments (size <= maxSize)
– Locate the fragments in gIndex tree
– Intersect the id lists associated with the fragments
• Apriori pruning
– Generating every fragment is inefficient
– If a fragment is not in gIndexTree, we need not check its super-graphs
any more
– Redundant fragments need to be recorded for Apriori pruning
f1
f2
f3
e1
e2
e3
Level 0
Level 1
Level 2
…
gIndex Tree
Query
<e1, e2, e3, e4, e5>
Fragments
<e1>
<e1, e2>
<e1, e2, e3>
<e1, e2, e3, e4>  stop
<e2>
… 16/50

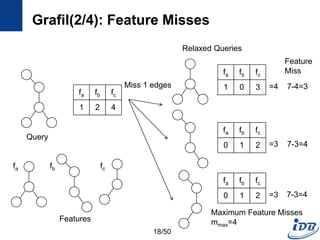
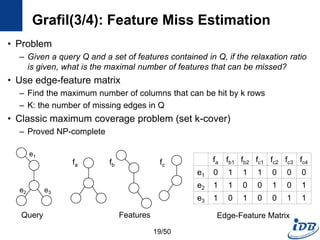
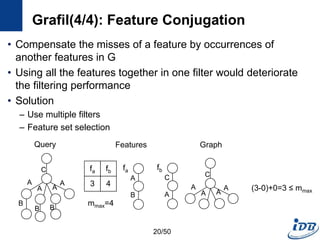
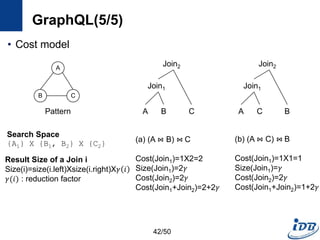
17. Grafil(1/4) [Yan et al., SIGMOD’05]
• Subgraph similarity search
• Feature-based approach
• Similarity search using relaxed queries
– Relax a query by deletion of k edges
– Missed edges incur missed features
• Main question
– What is the maximum missed features(𝑚 𝑚𝑎𝑥) when relaxing a query
with k missed edges?
Feature Vector
G1 {u1, u2, …, un}
G2
…
Gn
Subgraph exact search
Subgraph similarity search
𝑓𝑜𝑟 1 ≤ 𝑖 ≤ 𝑛, 𝑢𝑖 ≥ 𝑣𝑖
{v1, v2, …, vn}
𝑟 𝑢𝑖, 𝑣𝑖 =
0, 𝑖𝑓𝑢𝑖 ≥ 𝑣𝑖
𝑢𝑖 − 𝑣𝑖, 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
𝑖=1
𝑛
𝑟 𝑢𝑖, 𝑣𝑖 ≤ 𝑚 𝑚𝑎𝑥
Query
17/50

18. Grafil(2/4): Feature Misses
Query
Relaxed Queries
Features
fa fb fc
fa fb fc
1 2 4
fa fb fc
1 0 3
fa fb fc
0 1 2
fa fb fc
0 1 2
Miss 1 edges =4
=3
=3
Feature
Miss
7-4=3
7-3=4
7-3=4
Maximum Feature Misses
mmax=4
18/50

19. Grafil(3/4): Feature Miss Estimation
• Problem
– Given a query Q and a set of features contained in Q, if the relaxation ratio
is given, what is the maximal number of features that can be missed?
• Use edge-feature matrix
– Find the maximum number of columns that can be hit by k rows
– K: the number of missing edges in Q
• Classic maximum coverage problem (set k-cover)
– Proved NP-complete
Features
fa fb fc
Query
fa fb1 fb2 fc1 fc2 fc3 fc4
e1 0 1 1 1 0 0 0
e2 1 1 0 0 1 0 1
e3 1 0 1 0 0 1 1
Edge-Feature Matrix
e1
e2 e3
19/50

20. Grafil(4/4): Feature Conjugation
• Compensate the misses of a feature by occurrences of
another features in G
• Using all the features together in one filter would deteriorate
the filtering performance
• Solution
– Use multiple filters
– Feature set selection
Query Features
fafa fb
3 4
mmax=4
(3-0)+0=3 ≤ mmax
A
B
A A
A A
C
B
B B
fb
C
A
A A
A A
C
Graph
20/50

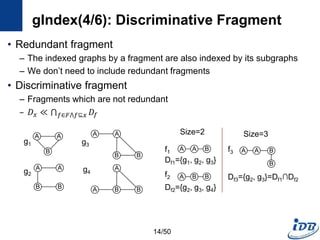
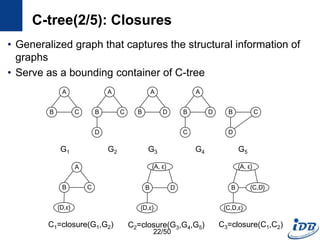
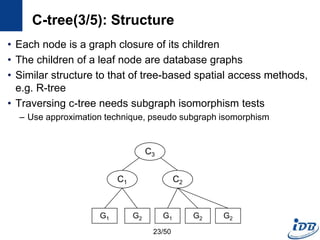
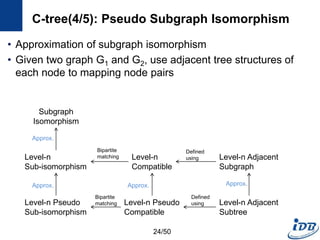
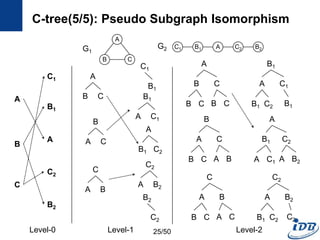
21. C-tree(1/5) [He and Singh, ICDE’06]
• Closure-tree
– Tree-based index
– Each node has graph closure of its descendants
– Support subgraph queries and similarity queries
• Pseudo subgraph isomorphism
– Perform pairwise graph comparisons using heuristic techniques
– Produce candidate answers within a polynomial time
C-tree
Query
Graph
Candidate
Graphs
21/50

22. C-tree(2/5): Closures
• Generalized graph that captures the structural information of
graphs
• Serve as a bounding container of C-tree
A
B C
A
B C
D
A
B D
A
B D
C
B C
D
G1 G2 G3 G4 G5
A
B C
{D,ε}
C1=closure(G1,G2)
{A, ε}
B D
{D,ε}
C2=closure(G3,G4,G5)
{A, ε}
B {C,D}
{C,D,ε}
C3=closure(C1,C2)
22/50

23. C-tree(3/5): Structure
• Each node is a graph closure of its children
• The children of a leaf node are database graphs
• Similar structure to that of tree-based spatial access methods,
e.g. R-tree
• Traversing c-tree needs subgraph isomorphism tests
– Use approximation technique, pseudo subgraph isomorphism
C3
C1 C2
G1 G2 G1 G2 G2
23/50

24. C-tree(4/5): Pseudo Subgraph Isomorphism
• Approximation of subgraph isomorphism
• Given two graph G1 and G2, use adjacent tree structures of
each node to mapping node pairs
Subgraph
Isomorphism
Level-n
Sub-isomorphism
Level-n
Compatible
Level-n Adjacent
Subgraph
Level-n Pseudo
Sub-isomorphism
Level-n Pseudo
Compatible
Level-n Adjacent
Subtree
Approx.
Approx. Approx. Approx.
Bipartite
matching
Bipartite
matching
Defined
using
Defined
using
24/50

25. C-tree(5/5): Pseudo Subgraph Isomorphism
A
B C
C1 B1 A C2 B2G1
G2
A
B
C
C1
B1
A
C2
B2
A
B C
B
A C
C
A B
B1
A C1
A
B1 C2
C2
A B2
C1
B1
B2
C2
A
B C
B C B C
B
A C
B C A B
C
A B
B C A C
B1
A C1
B1 C2 B1
A
B1 C2
A C1 A B2
C2
A B2
B1 C2 C2
25/50Level-0 Level-1 Level-2

26. QuickSI(1/6) [Shang et al., VLDB’08]
• Main paradigm for processing graph containment queries
– Filtering-and-verification framework
• Verification techniques
– Subgraph isomorphism testing
– Existing techniques are not efficient especially when the query graph
size becomes large
• Develop efficient verification techniques
26/50

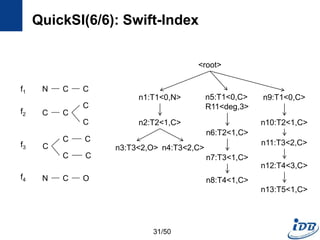
27. QuickSI(2/6): QI-Sequence
• A Sequence that represents a rooted spanning tree for a query q
– Encode a graph for efficient subgraph isomorphism testing
– Encode search order and topological information
– Have spanning entries and extra entries
• Spanning entry, Ti
– Keep basic information of the spanning tree
– Ti.v: record a vertex vk in a query graph q
– [Ti.p, Ti.l] : parent vertex and label of Ti.v
• Extra entry, Rij
– Extra topology information
– Degree constraint [deg : d] : the degree of Ti.v
– Extra edge [edge : j] : edge that doesn’t appear in the spanning tree
27/50

28. QuickSI(3/6): QI-Sequence
• Several QI-Sequences of one query graph, q
– Different search spaces when processing subgraph isomorphism testing
N C
C C
C
C C
Type [Ti.p, Ti.l] Ti.v
T1 [0, N] v1
T2 [1, C] v2
R21 [deg : 3]
T3 [2, C] v3
T4 [3, C] v4
T5 [4, C] v5
T6 [5, C] v6
T7 [6, C] v7
R71 [edge : 2]
Type [Ti.p, Ti.l] Ti.v
T1 [0, C] v4
T2 [1, C] v5
R61 [edge : 3]
T3 [2, C] v3
T4 [3, C] v6
T5 [4, C] v7
T6 [5, C] v2
T7 [6, C] v1
R61 [deg : 3]
Query
QI-Sequence, SEQq QI-Sequence, SEQq’
28/50

29. QuickSI(4/6): Effective QI-Sequence
• Constructing optimal QI-Sequence is hard
– Use heuristics to construct an effective QI-Sequence
• Calculate average inner supports of each distinct vertex and edge
– Average number of possible mappings in the graphs which contain the edge
or vertex
– Statistics information for graphs in the candidate set after filtering
• Convert q to a weighted graph qw
– w(e) = øavg(e), w(v)=øavg(v)
• Find minimum spanning tree in qw based on edge weights
N C
C C
C
C C
Weighted Graph
1.4
5.1
5.1
5.1
5.1 5.1
5.1
Edges
(N,C)
(C,C)
øavg(e)
1.4
5.1
Average Inner Support
29/50

30. QuickSI(5/6): Swift-Index
• Traditional filtering process
– Decompose the query graph into a set of features
– Identify every feature that also appears in the index
– Identification of a feature needs subgraph isomorphism
• Filtering using Swift-Index
– Pre-compute QI-Sequences for features
– Maintain QI-Sequences in a prefix-tree, Swift-Index
– Given a query graph q, search from the prefix-tree index in a top-down
fashion
– Reduce computational cost for subgraph isomorphism testing
30/50

31. QuickSI(6/6): Swift-Index
<root>
n1:T1<0,N>
n2:T2<1,C>
n3:T3<2,O> n4:T3<2,C>
n5:T1<0,C>
R11<deg,3>
n6:T2<1,C>
n7:T3<1,C>
n8:T4<1,C>
n9:T1<0,C>
n10:T2<1,C>
n11:T3<2,C>
n12:T4<3,C>
n13:T5<1,C>
N C C
C C
C
C
C
C
C
C C
N C O
f1
f2
f3
f4
31/50

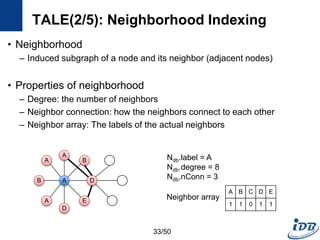
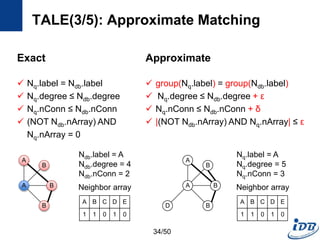
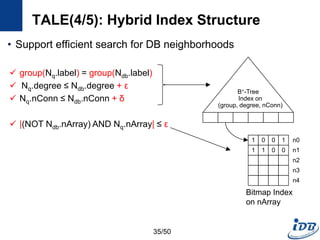
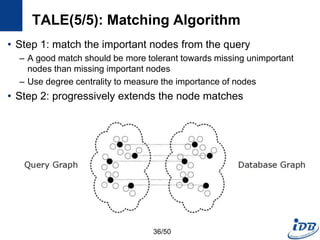
32. TALE(1/5) [Tian and Patel, ICDE’08]
• Motivation
– Need approximate graph matching
– Supporting large queries is more and more desired
• TALE (A Tool for Approximate Large Graph Matching)
– A Novel Disk-based Indexing Method
– High pruning power
– Linear index size with the database size
– Index-based matching algorithm
– Significantly outperforms existing methods
– Gracefully handles large queries and databases
32/50

33. TALE(2/5): Neighborhood Indexing
• Neighborhood
– Induced subgraph of a node and its neighbor (adjacent nodes)
• Properties of neighborhood
– Degree: the number of neighbors
– Neighbor connection: how the neighbors connect to each other
– Neighbor array: The labels of the actual neighbors
A
A
A
B
DB
A
D
E
Ndb.label = A
Ndb.degree = 8
Ndb.nConn = 3
A CB ED
1 01 11
Neighbor array
33/50

34. TALE(3/5): Approximate Matching
Exact
 Nq.label = Ndb.label
 Nq.degree ≤ Ndb.degree
 Nq.nConn ≤ Ndb.nConn
 (NOT Ndb.nArray) AND
Nq.nArray = 0
Approximate
 group(Nq.label) = group(Ndb.label)
 Nq.degree ≤ Ndb.degree + ε
 Nq.nConn ≤ Ndb.nConn + δ
 |(NOT Ndb.nArray) AND Nq.nArray| ≤ ε
A
A
B
B
B
Ndb.label = A
Ndb.degree = 4
Ndb.nConn = 2
A CB ED
1 01 01
Neighbor array A
A
B
B
D B
Nq.label = A
Nq.degree = 5
Nq.nConn = 3
A CB ED
1 01 01
Neighbor array
34/50

35. TALE(4/5): Hybrid Index Structure
• Support efficient search for DB neighborhoods
 group(Nq.label) = group(Ndb.label)
 Nq.degree ≤ Ndb.degree + ε
 Nq.nConn ≤ Ndb.nConn + δ
 |(NOT Ndb.nArray) AND Nq.nArray| ≤ ε
B+-Tree
Index on
(group, degree, nConn)
1 0 0 1
1 1 0 0
n0
n1
n2
n3
n4
Bitmap Index
on nArray
35/50

36. TALE(5/5): Matching Algorithm
• Step 1: match the important nodes from the query
– A good match should be more tolerant towards missing unimportant
nodes than missing important nodes
– Use degree centrality to measure the importance of nodes
• Step 2: progressively extends the node matches
36/50

37. Outline
• Category of graph queries
• Querying in collection DB
• Querying in large graphs
• References
37/50

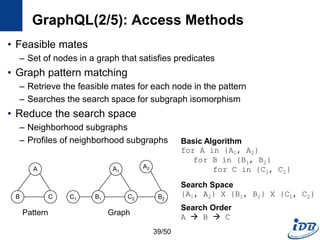
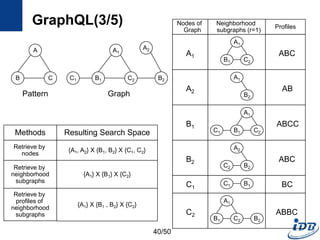
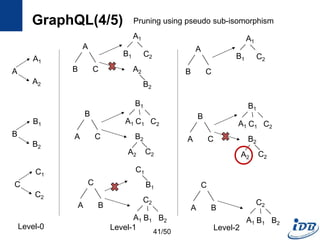
38. GraphQL(1/5) [He and Singh, SIGMOD’08]
• Motivation
– Need a language to query and manipulate graphs with arbitrary attributes
and structures
– Native access methods that exploit graph structural information
• Formal language for graphs
– Notion for manipulating graph structures
– Basis of graph query language
– Concatenation, disjunction, repetition
• Graph query language
– Subgraph isomorphism + predicate evaluation
graph G1 {
node v1, v2, v3;
edge e1 (v1, v2);
edge e2 (v2, v3);
edge e3 (v3, v1);
}
v1
v2 v3
e1 e3
e2
graph P {
node v1, v2;
edge e1 (v1, v2);
} where v1.name = “A”
and v2.year > 2000;
Graph motif Graph pattern
38/50

39. GraphQL(2/5): Access Methods
• Feasible mates
– Set of nodes in a graph that satisfies predicates
• Graph pattern matching
– Retrieve the feasible mates for each node in the pattern
– Searches the search space for subgraph isomorphism
• Reduce the search space
– Neighborhood subgraphs
– Profiles of neighborhood subgraphs
B
A
C B1
A1
C2C1 B2
A2
Pattern Graph
Basic Algorithm
for A in {A1, A2}
for B in {B1, B2}
for C in {C1, C2}
Search Space
{A1, A2} X {B1, B2} X {C1, C2}
Search Order
A  B  C
39/50

40. GraphQL(3/5)
B
A
C B1
A1
C2C1 B2
A2
Pattern Graph
B1
A1
C2
A1 ABC
Nodes of
Graph
Neighborhood
subgraphs (r=1)
Profiles
A1
B2
A2 AB
B1
A1
C2
B1 ABCC
C2
A2
B2
B2 ABC
C1 B1C1 BC
B1
A1
C2
C2 ABBC
C1
B2
Resulting Search Space
Retrieve by
nodes
Methods
{A1, A2} X {B1, B2} X {C1, C2}
Retrieve by
neighborhood
subgraphs
{A1} X {B1} X {C2}
Retrieve by
profiles of
neighborhood
subgraphs
{A1} X {B1 , B2} X {C2}
40/50

41. GraphQL(4/5)
A
A1
A2
B
B1
B2
C
C1
C2
A
B C
A1
B1 C2
A2
B2
B
A C
B1
A1 C1
B2
C2
C
A B
C2
A2
C1
B1
C2
A1 B1 B2
A
B C
A1
B1 C2
B
A C
B1
A1 C1
B2
C2
C
A B
C2
A2
C2
A1 B1 B2
41/50
Level-0 Level-1 Level-2
Pruning using pseudo sub-isomorphism

42. GraphQL(5/5)
• Cost model
Join2
Join1
A B C
Join2
Join1
A C B
B
A
C
Pattern
Search Space
{A1} X {B1, B2} X {C2} (a) (A ⋈ B) ⋈ C
Cost(Join1)=1X2=2
Size(Join1)=2𝛾
Cost(Join2)=2𝛾
Cost(Join1+Join2)=2+2𝛾
(b) (A ⋈ C) ⋈ B
Cost(Join1)=1X1=1
Size(Join1)=𝛾
Cost(Join2)=2𝛾
Cost(Join1+Join2)=1+2𝛾
Result Size of a Join i
Size(i)=size(i.left)Xsize(i.right)X𝛾 𝑖
𝛾(𝑖) : reduction factor
42/50

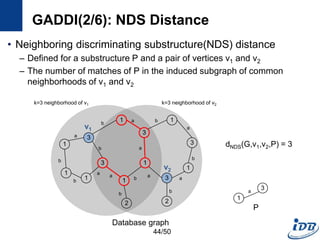
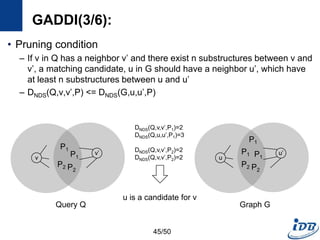
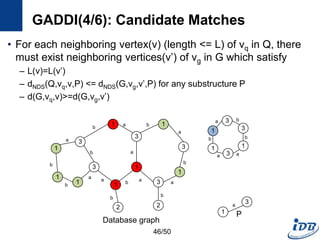
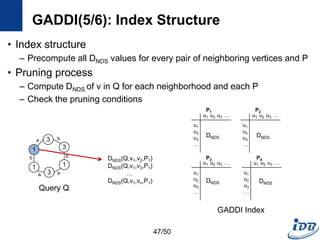
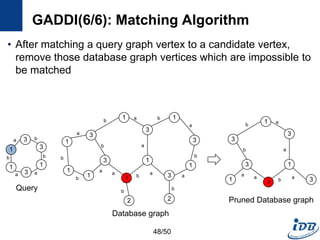
43. GADDI(1/6) [Zhang et al., EDBT’09]
• Employ novel indexing method, NDS distance
– Capture the local graph structure between each pair of vertices
– More pruning power than indexes which are based on information of one
vertex
• Matching algorithm based on two-way pruning
– Candidate matching using NDS distance
– Remove impossible vertices after some vertices are matched
43/50

44. GADDI(2/6): NDS Distance
• Neighboring discriminating substructure(NDS) distance
– Defined for a substructure P and a pair of vertices v1 and v2
– The number of matches of P in the induced subgraph of common
neighborhoods of v1 and v2
44/50
1
1
1
3
3
1
3
1
3
1
3
1
1
2 2
Database graph
3
1
P
a
a
a
a
a a
a
a
a
b
b
b
b
b
b
b
b
b
k=3 neighborhood of v1 k=3 neighborhood of v2
3
1
3
1
1
v1
v2
dNDS(G,v1,v2,P) = 3

45. GADDI(3/6):
• Pruning condition
– If v in Q has a neighbor v’ and there exist n substructures between v and
v’, a matching candidate, u in G should have a neighbor u’, which have
at least n substructures between u and u’
– DNDS(Q,v,v’,P) <= DNDS(G,u,u’,P)
45/50
v
v’
P1
P1
P2 P2
Query Q
u
u’P1 P1
P2 P2
Graph G
P1
DNDS(Q,v,v’,P1)=2
DNDS(Q,u,u’,P1)=3
DNDS(Q,v,v’,P2)=2
DNDS(Q,v,v’,P2)=2
u is a candidate for v

46. GADDI(4/6): Candidate Matches
• For each neighboring vertex(v) (length <= L) of vq in Q, there
must exist neighboring vertices(v’) of vg in G which satisfy
– L(v)=L(v’)
– dNDS(Q,vq,v,P) <= dNDS(G,vg,v’,P) for any substructure P
– d(G,vq,v)>=d(G,vg,v’)
46/50
1
1
1
3
3
1
3
1
3
1
3
1
1
2 2
a
a
a
a
a a
a
a
b
b
b
b
b
b
b
b
b
3
1 P
a
1
1
3
3
1
3
b
b
a
b
a
a
1
1
1
1 1
1
1
1
1
1
1
Database graph

47. GADDI(5/6): Index Structure
• Index structure
– Precompute all DNDS values for every pair of neighboring vertices and P
• Pruning process
– Compute DNDS of v in Q for each neighborhood and each P
– Check the pruning conditions
47/50
P1
u1 u2 u3 …
u1
u2
u3
…
P2
u1 u2 u3 …
u1
u2
u3
…
P3
u1 u2 u3 …
u1
u2
u3
…
P4
u1 u2 u3 …
u1
u2
u3
…
DNDS
DNDS
DNDS
DNDS
1
1
3
3
1
3
b
b
a
b
a
a
Query Q
GADDI Index
DNDS(Q,v1,v2,P1)
DNDS(Q,v1,v3,P1)
…
DNDS(Q,v1,vn,P1)

48. GADDI(6/6): Matching Algorithm
• After matching a query graph vertex to a candidate vertex,
remove those database graph vertices which are impossible to
be matched
48/50
1
1
1
3
3
1
3
1
3
1
3
1
1
2 2
a
a
a
a
a a
a
a
b
b
b
b
b
b
b
b
b
1
3
3
1
3
3
1
1
a
a
a
a a
b
b
b
1
1
3
3
1
3
b
b
a
b
a
a
Database graph
Pruned Database graph
Query

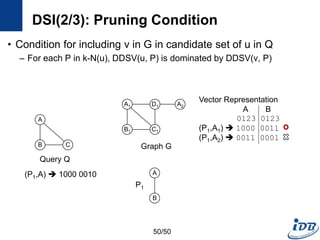
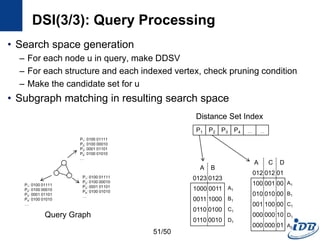
49. DSI(1/3) [Kou et al., WAIM’10]
• Discriminative structure
• Distance set
– Distinct distances of all the path between a vertex, v and substructures
in k-N(v)
– The path must not contain an edge in P
49/50
A1
B1
D1
C1
A2
A
B
Graph G
P1
A1
B1
Distance (k=3)
P1.A  A1 : 0
P1.B  A1 : 2, 3
P1.A  A2 : 2, 3
P1.B  A2 : 3, (4)
Vector Representation
A B
0123 0123
(P1,A1)  1000 0011
(P1,A2)  0011 0001

50. DSI(2/3): Pruning Condition
• Condition for including v in G in candidate set of u in Q
– For each P in k-N(u), DDSV(u, P) is dominated by DDSV(v, P)
50/50
Vector Representation
A B
0123 0123
(P1,A1)  1000 0011
(P1,A2)  0011 0001
A1
B1
D1
C1
A2
Graph G
A
B C
(P1,A)  1000 0010
Query Q
A
B
P1

51. DSI(3/3): Query Processing
• Search space generation
– For each node u in query, make DDSV
– For each structure and each indexed vertex, check pruning condition
– Make the candidate set for u
• Subgraph matching in resulting search space
51/50
Query Graph
P1: 0100 01111
P2: 0100 00010
P3: 0001 01101
P4: 0100 01010
…
P1: 0100 01111
P2: 0100 00010
P3: 0001 01101
P4: 0100 01010
…
P1: 0100 01111
P2: 0100 00010
P3: 0001 01101
P4: 0100 01010
…
P1 P2 P3 P4 … …
A B
0123 0123
1000 0011
0011 1000
0110 0100
0110 0010
A1
B1
C1
D1
A C D
012 012 01
100 001 00
010 010 00
001 100 00
000 000 10
000 000 01
A1
B1
C1
D1
A2
Distance Set Index

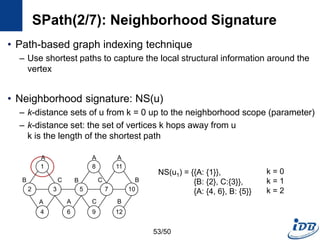
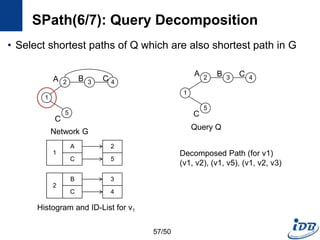
52. SPath(1/7) [Zhao and Han, VLDB’10]
• Problems of previous graph matching methods
– Designed on special graphs
– Limited guarantee on query performance and scalability support
– Lack of scalable graph indexing mechanisms and cost-effective graph
query optimizer
• SPath
– Compact indexing structure using local structural information of vertices:
neighborhood signatures
– Query processing: vertex-at-a-time to path-at-a-time
• Target graph
– Connected, undirected simple graphs with no edge weights
– Labeled vertices
52/50

53. SPath(2/7): Neighborhood Signature
• Path-based graph indexing technique
– Use shortest paths to capture the local structural information around the
vertex
• Neighborhood signature: NS(u)
– k-distance sets of u from k = 0 up to the neighborhood scope (parameter)
– k-distance set: the set of vertices k hops away from u
k is the length of the shortest path
NS(u1) = {{A: {1}},
{B: {2}, C:{3}},
{A: {4, 6}, B: {5}}
k = 0
k = 1
k = 2
1
2 3
4
5
6
8
7
9
11
10
12
A
B C
A A
B
A A
C B
C B
53/50

54. SPath(3/7): NS Containment
• 𝐺𝑖𝑣𝑒𝑛 𝑢 ∈ 𝑉 𝐺 𝑎𝑛𝑑 𝑣 ∈ 𝑉 𝑄 , 𝑁𝑆 𝑣 𝑖𝑠 𝑐𝑜𝑛𝑡𝑎𝑖𝑛𝑒𝑑 𝑖𝑛 𝑁𝑆 𝑢 , 𝑑𝑒𝑛𝑜𝑡𝑒𝑑 𝑎𝑠 𝑁𝑆 𝑣 ⊑
𝑁𝑆 𝑢 , 𝑖𝑓 ∀𝑘 ≤ 𝑘0, ∀𝑙 ∈ Σ, 𝑘≤𝑘0
𝑆 𝑙
𝑘
(𝑣) ≤ 𝑘≤𝑘0
𝑆 𝑙
𝑘
(𝑢)
• We can safely prune u1 from C(v1)
NS(u1) = {{A: {1}},
{B: {2}, C:{3}},
{A: {4, 6}, B: {5}}
k = 0
k = 1
k = 2
NS(v1) = {{A: {1}},
{B: {2}, C:{3}},
{C: {4}}
k = 0
k = 1
k = 2
Network G
Query Graph G
𝑁𝑆 𝑣1 ⋢ 𝑁𝑆 𝑢1
1
2 3
4
5
6
8
7
9
11
10
12
A
B C
A A
B
A A
C
C B
2
1 4
3
B
A C
C
54/50

55. SPath(4/7): Implementation
• Lookup table
– 𝛨: 𝑙∗
→ 𝑢 𝑙 𝑢 = 𝑙∗
, 𝑙∗
∈ Σ
– Easily figure out matching candidates
• Histogram
– Succinct distance-wise histogram 𝑆 𝑘
𝑙
(𝑢) for 𝑘 < 0 ≤ 𝑘0
• ID-List
– Exact vertex identifiers in 𝑆 𝑘
𝑙
(𝑢)
• Lookup table and histograms are stored in main memory
• ID-Lists are on disk
Global Lookup Table
Network G
Histogram and ID-List
for v3
1
2 3
4
5
6
8
7
9
11
10
12
A
B C
A A
B
A A
C B
C B
label
A
vid
1
B
C
2
3
4
5
7
6
10
9
8
12
11
distance label count
A 3
1
B 2
A 1
2
C 2
vid
1
2
8
7
4
5
9
6
55/50

56. SPath(5/7): Graph Query Processing
• Compute NS(v) for each 𝑣 ∈ 𝑉 𝑄
• Pruning
– Examine matching candidates C(v)
– NS containment testing
– Reduced matching candidates of v: C’(v)
• Query decomposition
– Select shortest paths of Q which are also shortest path in G
• Path selection and join
– Reconstruct Q
– Selected shortest paths should be cost-effective
56/50

57. SPath(6/7): Query Decomposition
• Select shortest paths of Q which are also shortest path in G
1
2
5
3
A B
C
1
2
5
4A C
C
Network G
Query Q
B
1
A
B
C
2
3
5
2
3
C 4
4C
Decomposed Path (for v1)
(v1, v2), (v1, v5), (v1, v2, v3)
Histogram and ID-List for v1
57/50

58. SPath(7/7): Path Selection
• Given a join path
• Total join cost
• Selectivity
– is a function of path length
58/50

59. References
• [Shasha et al., PODS’02] Dennis Shasha, Jaso T. L. Wang, Rosalba Giugno,
Algorithmics and Applications of Tree and Graph Searching. PODS, 2002.
• [Yan et al., SIGMOD’04] Xifeng Yan, Philip S. Yu, Jiawei Han, Graph Indexing:
A Frequent Structure-based Approach. SIGMOD, 2004.
• [Yan et al., SIGMOD’05] Xifeng Yan, Philip S. Yu, Jiawei Han, Substructure
Similarity Search in Graph Databases. SIGMOD, 2005.
• [Tian and Patel, ICDE’08] Yuanyuan Tian , Jignesh M. Patel. TALE: A Tool for
Approximate Large Graph Matching. ICDE, 2008.
• [He and Singh, SIGMOD’08] Huahai He, Ambuj K. Singh. Graphs-at-a-time:
query language and access methods for graph databases. SIGMOD, 2008.
• [Zhao and Han, VLDB’10] Peiziang Zhao, Jiawei Han. On Graph Query
Optimization in Large Networks. VLDB, 2010.
• [He and Singh, ICDE’06] Huahai He, Ambuj K. Singh, Closure-Tree: An Index
Structure for Graph Queries. ICDE, 2006
• [Shang et al., VLDB’08] Haichuan Shang, Ying Zhang, Xuemin Lin, Jeffrey Xu
Yu, Taming Verification Hardness: An Efficient Algorithm for Testing Subgraph
Isomorphism. VLDB, 2008
59/50

60. References
• [Zhang et al., EDBT’09] Shijie Zhang, Shirong Li, Jiong Yang,
GADDI: Distance Index based Subgraph Matching in
Biological Networks. EDBT, 2009
• [Zhang et al., CIKM’10] Shijie Zhang, Shirong Li, Jiong Yang,
SUMMA: Subgraph Matching in Massive Graphs. CIKM, 2010
• [Kou et al., WAIM’10] Yubo Kou, Yukun Li, Xiaofeng Meng,
DSI: A Method for Indexing Large Graphs Using Distance Set.
WAIM, 2010
60/50