東京大学松尾研究室におけるPRML輪読資料です。

1. PRML輪読会 2017
第7章 疎な解を持つカーネルマシン
東京⼤学⼤学院⼯学系研究科
技術経営戦略学専攻
松尾研究室
⼤野峻典

2. 構成
7.1 最⼤マージン分類器
7.2 関連ベクトルマシン
2

3. 疎な解を持つカーネルマシン
• 6章における問題：カーネル関数をすべての訓練データ対について計算しな
ければいけないため、学習および予測時に計算時間が⼤きくなりうる
• → 7章：疎な解を持ち、訓練データ点の⼀部だけに対してカーネル関数を計
算することで新しい⼊⼒の予測ができるアルゴリズムを考える。
3

4. 7章の概要
• 最⼤マージン分類器
– 特徴空間において線形分離可能な場合の⾮線形SVM
• 重なりのあるクラス分布
– 特徴空間において線形分離不可能な場合の⾮線形SVM
• 多クラスSVM・回帰のためのSVM
– 本来2クラス分類を⽬的としたSVMを多クラス分類や回帰に応⽤する⽅法
• 関連ベクトルマシン（RVM）
– 事後確率分布を求めることが可能
– SVMよりもさらに疎なモデルが得られる
4

5. 7.1 最⼤マージン分類器
• まず以下の線形モデルを⽤いて2値分類問題を解くことから考える。
– ⼊⼒ベクトル： x1,…,xN
– ⽬標値：t1,…,tN (tn ∈{-1,1})
– 未知のデータ点xはy(x)の符号に応じて分類
– 訓練データは特徴空間で線形分離可能と仮定
• 4.1.7節におけるパーセプトロンでは…
– 有限の計算ステップで解を⾒つけることを保証
– 解はwとbの（任意の）初期値や、訓練データ点を⼊⼒する依存するので、⼀意に定ま
るとは限らない
• → 訓練データを正確に分離する解が複数存在する場合、汎化誤差が最⼩に
なるような解を求めたい…SVM！
– SVMはマージンという、分類境界と訓練データ間の最短距離を指す概念を⽤いる.
5

6. 7.1 最⼤マージン分類器
6
• 直感的にマージンが最⼤になるところが汎化誤差最⼩になりそう.
– 厳密な理由は、計算論的学習理論、統計的学習理論で説明できる.
• 分類境界近くの⼀部のデータ（サポートベクトル）により、分類境界の位置
が決まる.
– 最適な分類境界の変わりに、学習済みの密度モデルの確率分布の下で誤りが最⼩になる
ことを考えてみると、
– 各クラスごとの⼊⼒ベクトルの分布が共通のσ2を持つとき、σ2→0の極限に於いて、最
適解は、マージンを最⼤化する超平⾯と⼀致する。
– 直感的にはσ2が⼩さくなるに連れて、分離表⾯は遠⽅のデータ点よりも近傍の近くに強
く影響されるようになりσ2→0の極限においては、サポートベクトル以外の点とは独⽴
に分離平⾯がさだまるようになる。

7. 7.1 最⼤マージン分類器
• 図4.1より, 分離境界から点xまでの距離は、以下のようにかける.
• マージンは訓練データと分類境界の最短距離で、そのマージンを最⼤化する
パラメータwとbを知りたいので、以下の最適化問題を解けばいい.
• 直接解くのは⾮常に複雑… → より簡単な形に変形する.（2次最適化問題）
– パラメータw→κw, b→κbのように定数倍（ (7.2)より点xから分類境界の距離は変化し
ない）し、境界に最も近い点について、以下の式を成⽴させる.
– このとき、すべてのデータに関して次の制約式が成⽴する.
7

8. 7.1 最⼤マージン分類器
• (続き) このようにスケーリングした識別関数は正規形と⾔われる.
– (7.5)の等式が整理する場合：制約は有効, それ以外: 制約は無効 と⾔われる.
• すなわち、以下の2次最適化問題を解けばいい.
– ⽬的関数：
– 制約条件：
• この制約付き最適化問題を解くため, (7.5)の各制約式ごとにラグランジュ
定数an>=0 (⇛付録E)を導⼊すると、次のラグランジュ関数が得られる。
• L(w,b,a)をwとbについて微分した後、0に等しいとして以下の条件得る.
8

9. (補⾜) ラグランジュ未定乗数法
• ラグランジュの未定乗数法の解説と直感的な証明 より
9

10. 7.1 最⼤マージン分類器
• (続き) (7.8), (7.9)をL(w,b,a)に代⼊し, wとbを消去すると,⽬的関数であ
る(7.6)の双対表現が得られる. (カーネル関数で表現.)
– この⽬的関数をaに対して最⼤化すれば良い.
– ただし, aは以下の制約条件を満たす.
– 再び⼆次計画法(ただし, 最適化変数はaに変わった)になっている.
– モデルをカーネルで表現できるようになるので、特徴空間の次元がデータ点の数を上回
るような場合でも、最⼤マージン分類器を効率的に適⽤できるようになる.
10

11. 7.1 最⼤マージン分類器
• (7.1)のy(x)は, wを(7.8)で置き換えることで, パラメータ{an}とカーネル
関数で表される.
• KKT条件(⇛ 付録E)を適⽤すると、次の3条件が成⽴.
– なお、全てのデータ点についてan=0あるいはtny(xn)=1が成⽴.
– an=0 となるデータ点は(7.13)中の和から消えるので、新しいデータ点の予測に対して
何も影響しない.
– an≠0となるデータ点は、サポートベクトルと呼ばれる. (図7.1)
• モデルを⼀度学習してしまえば、サポートベクトル以外の訓練データの情報
は不要となるという点で実⽤的.
11

12. 7.1 最⼤マージン分類器
• ⼆次計画問題を解きaが求まると, バイアスパラメータbが求まる. 具体的に
は、任意のサポートベクトルxnはtny(xn)=1を満たすことを踏まえると,
(7.13)から次の式が成⽴
– Sはサポートベクトルの添え字からなる集合. すべてのサポートベクトルに対して平均
を取って, 以下のようにb求まる.
– Nsはサポートベクトルの総数.
• 他のモデルと⽐較するために、最⼤マージン学習は, 単純な⼆次正則化項を
伴った誤差関数の最⼩問題として次のように表現してみる.
– E∞(z)は、z>=０の時0, それ以外の場合は∞で、制約条件(7.5)満たすことを保証.
12

13. 7.1 最⼤マージン分類器
• 簡単な⼈⼯データを(6.23)のガウスカーネルを⽤いたSVMを訓練して分類
した結果が以下.
– xの⼆次元空間では線形分離可能でないが、⾮線形なカーネルによって定められている
⾮線形な特徴空間においては線形分離されている.
• SVMの解はサポートベクトル以外のデータには全く依存しない疎な解とな
ることが幾何学的にもわかる.
– 最⼤マージンの分類境界は、サポートベクトルの位置によってのみ決まり、それ以外の
データ点はどこに動かしても、分類境界に影響を与えないため.
13

14. 7.1.1 重なりのあるクラス分類
14
• これまで：訓練データ点が特徴空間Φ(x)において線形分離可能であり, SVM
はもともとの⼊⼒空間xにおいて訓練データを完全に分類すると仮定してき
た.
– 誤って分類したデータについては無限⼤のペナルティを与え、正しく分類したデータに
はペナルティ与えない誤差関数を⽤いてた. (7.19)
– しかし…、実際の問題においてはクラスの条件付き確率分布が重なる場合ありえる.
• ⼀部の訓練データの誤分類を許すようにSVMを修正する.
– データ点がマージン内に侵⼊した場合には、マージン境界からの距離に応じたペナル
ティを与えることで、マージン境界の「間違った側」に存在することを許すように定式
化を修正.

15. 7.1.1 重なりのあるクラス分類
15
• スラック変数
– 各訓練データごとに定義される変数
– 定義(ξ: “グザイ”)
• データが正しく分類されかつマージン境界の上/外側に存在する場合: ξn=0
• それ以外: ξn=|tn-y(xn)| と定義
– したがって、ちょうど分類境界y(x)=0上にあるデータは, ξn=1、誤分類されたデータ
についてはξn>1, マージン内部にあるが正しく分類されている時は 0<ξn<=1が成⽴.
• 識別関数(7.5)は、次のように修正できる
• ハードマージンの制約のソフトマージンへの緩和、と呼ばれる
– ⼀部の訓練データの誤分類を許し、クラス分布に重なりがあるときにもSVMが適⽤可能
になる.

16. 7.1.1 重なりのあるクラス分類
16
• ⽬的：マージン境界に対して誤った側に存在する点に対して「ソフトに」ペ
ナルティを与えつつ、マージンを最⼤化.
• 最⼩化する⽬的関数：
– C>0はスラック変数をもちいて表されるペナルティと、マージンの⼤きさの間のトレー
ドオフを制御するパラメータ.
• Σξnは誤分類されたデータの上限（誤分類ではξn>1なので）
• したがって, Cは訓練エラーとモデルの複雑さのトレードオフを制御する正則化係数（の逆
数）と似た役割を果たしているとわかる.
• 実際, C→∞では, 分離可能なデータに対するハードマージンSVMの最適化問題と等しくなる.
• 制約条件：(7.20)とξn>=0
• この最⼩化問題のラグランジュ関数は以下. (an>=0, μn>=0はラグランジュ乗数)
– KKTは以下で与えられる.

17. 7.1.1 重なりのあるクラス分類
17
• 今, y(x)の定義式(7.1)を⽤いて, w,b,{ξn}についての停留条件を変形する.
• 結果をラグランジュ関数に代⼊すると双対形のラグランジュ関数が得られる.
– 制約条件の違いを除き、分離可能な場合のラグランジュ関数と同⼀.
– ここでan>=0が成り⽴ち, μn>=0 からan<=Cが成り⽴つ.
– よって、(7.32)を次の条件下で最⼩化する双対関数{an}を求めればいい.
←短形制約と呼ばれる

18. 7.1.1 重なりのあるクラス分類
18
• (つづき) ソフトマージンSVMの最適化問題は再び⼆次計画化問題になって
いる.
– 新しいデータ点予測には, ハードマージン同様(7.13)を⽤いればいい.
• 得られた解について、an=0となる⼀部のデータ点は識別関数(7.13)に影響
せず、それ以外のデータ点がサポートベクトルとなる. サポートベクトルで
は an > 0で、(7.25)より以下が成⽴する.
• an<Cが成り⽴つ場合
– (7.31)よりμn>0であり, そして(7.28)より, ξn=0が成⽴するので、ちょうどマージン
境界上に存在することがわかる.
• an=Cが成り⽴つ場合
– 同様の議論により、データ点はマージン内に侵⼊しており, ξn<= 1の場合は正しく分類,
ξn>1の場合は誤分類されていることがわかる.
• パラメータbの計算
– 0<an<Cとなるサポートベクトルでは、ξn=0が成り⽴ち, tny(xn)=1が成⽴するので,
(7.1)のパラメータbは、以下のように計算できる. (ここでも同様にサポートベクトルの平均とる)

19. 7.1.1 重なりのあるクラス分類
19
• 異なる定式化の⽅法も提案されている(Scholkopf et al. 2000)
– 制約関数：
– ポイント：Cの代わりのパラメータγが訓練データに占めるマージン誤差(ξn>0)の割合
の上限（=サポートベクトルの割合の下限）として解釈できる.

20. 7.1.1 重なりのあるクラス分類
20
• パラメータ学習段階では全ての訓練データの情報が必要となるので、実⽤上
はSVMの⼆次計画法を効率的に解くアルゴリズムが存在することが重要.
– (7.10), (7.32)の⽬的関数L(a)は⼆次で, かつ, 制約条件が定める可能性の領域が凸な
ので, 任意の局所解が⼤局解となる.
• 伝統的な⼆次計画法のアルゴリズムは計算コスト、メモリ使⽤量的にダメ.
• チャンキング(Vapnik, 1982)
– カーネル⾏列からラグランジュ乗数が0となるデータに対応する⾏および列を取り除い
ても、ラグランジュ関数が不変であることを利⽤した⼿法.
– より次元数の⼩さな問題を順に解き、最終的には0とならないラグランジュ乗数だけ残
す.
– 保護共益勾配法を⽤いて実装できる.
• 分解法(Osuna et al, 1996)
– データが⼤規模でチャンキングでもメモリ乗らない時のために.
– サイズの⼩さな⼆次計画問題を繰り返し解く. (ここはチャンキングと同じ)
– 個々の部分問題の⼤きさが⼀定. → 任意の⼤きさのデータに適⽤できる.
• 逐次最⼩問題最適化法/SMO(Platt, 1999)
– 分解法でも部分⼆次計画問題解くのに数値計算コスト⾼い.
– たった2つのラグランジュ乗数を含む部分問題を逐次解くことで最適解得る.
– 変数2つなので数値計算⽤いず解析的に解け、⾼速.

21. 7.1.1 重なりのあるクラス分類
21
• SVMは新しい⼊⼒ベクトルに対して分類を⾏うのみで、確率的な予測はし
ない.
– → SVMを確率的な予測システムの⼀部として⽤いる場合、新しい⼊⼒xがクラスtに分
類される確率を計算することは必須.
• Platt(2000)
– 訓練済みのロジスティックシグモイド関数をSVMの出⼒に適⽤することで、この問題を
解決しようとした. 具体的には、求めたい条件付き確率が次の形を取ると仮定した.
– y(x)は(7.1)で定義される識別関数. パラメータA,Bはある訓練データ上でy(xn)とtnの
クロスエントロピー誤差関数が最⼩になるよう定める.
– 過学習を避けるために、SVMを学習するときに⽤いたデータと独⽴なものを求める.

22. 7.1.2 ロジスティック回帰との関係
22
• 分離可能な場合と同様に、分離不可能なデータ分布についても正則化項を含
む誤差関数の最⼩化という形で、SVMを定式化できることを⾒てきた.
• この定式化を通してロジスティック回帰モデルとの関係を議論でき
る.(4.3.2)
• ⽬的関数：
– ただし, ヒンジ形誤差関数：
• []+は引数が正のときはそのまま、それ以外のときは0を出⼒.
• 図7.5よりヒンジ形誤差関数は誤分類誤差関数の近似と⾒ることができる.
– 誤分類誤差関数は本来最⼩化したい量

23. 7.1.2 ロジスティック回帰との関係
23
• ロジスティック回帰の尤度関数の式を⽬標変数 t ∈ {-1, 1} を⽤いて定式
化しなおす. (SVMと⽐較するため⽬標変数合わせてる.)
– y(x) は(7.1)の関数, σ(y) を(4.59)で定義し、 p(t=1|y)=σ(y) が成り⽴つ.
– p(t=-1|y)=1-σ(y)=σ(-y) が成⽴するので、p(t|y)=σ(yt) が成⽴.
– 対数尤度の符号を反転したものと2次の正則化項を加え以下の⽬的関数を得る.
• 定数倍して点(0,1)を通過するようにすると、SVMの誤差関数と似た形にな
ることがわかる(図7.5)
– 違い：Esv(yt)は平坦な領域を持つため、より疎な解を得やすい.
• ロジスティック回帰の誤差関数もヒンジ形誤差関数もともに、誤分類誤差を
連続関数で近似したものと考えられる.
• 誤分類率を最⼩化することが⽬的な場合は、単調に減少する誤差関数を使⽤
したい (ex. ヒンジ形誤差関数, ロジスティック回帰の誤差関数)
– これらの他の誤差関数として⼆乗誤差もあるが、⼆乗誤差は、正しく分類されていても
分類境界から遠いとペナルティ課してしまうため、逆に誤分類を増やしかねない.

24. 7.1.3 多クラスSVM
24
• SVMは本来2クラス分類機だが、実際には2クラス以上の多クラス問題を解
く必要ある場合も多い.
– 2クラスSVMを複数組み合わせて、多クラス分類器を実現する⽅法が⾊々提案されてる.
• 1対他⽅式
– K個のクラスがあるときにあるクラスCkに属するデータを正例、それ以外のデータを負
例としてK個の別々のSVM yk(x)を学習する⽅法.
– 問題１: 個々のSVMによる予測が⽭盾し、⼀つの⼊⼒に複数のクラスが割り当てられる
可能性.
• 対応策として、最も⼤きな識別関数の値を返すクラスを予測値とすることがあるが、各SVM
は独⽴な分類問題を解くように学習しているので、yk(x)の値を⽐較することが意味持つとい
う保証はない.
– 問題2：訓練データの正例と負例のバランスが悪い.
• もとの問題に存在する対称性を失う；例. 10クラスで同じだけの数の訓練データ持つ時、各
分類器では90%が負例で、残り10％だけ正例となるような訓練データで学習することになる.
• 対応策として、Lee et al.(2001)では、正例に対する識別関数の値は+1で、負例に対しては
-1/(K-1)となるように学習することを提案している.
• Weston and Watkins(1999)
– 各クラスと他のクラス全体のマージンが最⼤になるように⼀つの⽬的関数を定め、K個
のSVMを⼀度に学習する⽅法.
– 問題：この⽅法では O(K2N2)と、時間かかる. (１対他⽅式では, O(KN2).)

25. 7.1.3 多クラスSVM
25
• 1対1⽅式
– 全てのクラスの組み合わせについて2クラスSVMを学習し、得られたK(K-1)/2個の分類
器を適⽤して、最も多くの分類器を正例として「投票」して決める.
– 問題1: 分類クラスが⼀意に定まらない場合も.
– 問題2：Kが⼤きい場合学習時間⼤幅増加. 予測にかかる計算時間も⼤きい. (1対他⽅式
と⽐べ)
• DAGSVM (Platt et al.(2000))
– ⼀対⼀⽅式の予測時間を削減するために有向⾮循環グラフで表現される順で分類器をて
要する.
– 新しいテスト点の分類にK(K-1)/2個の分類器のうちK-1個だけを適⽤する.
• Dietterich and Bakiri(1995) & Allwein et al. (2000)
– 誤り訂正出⼒符号を利⽤して、⼀般に多クラス分類問題を2クラス分類問題に帰着する
⽅法を提案. その⽅法をSVMに適⽤.
– まず, クラス集合を適当な⽅法で2分割し, ⼀⽅に属するクラスのデータを正例, もう⼀
⽅を負例として分類器を学習. 次に, 違った分割⽅法で正負例を作り, 学習を⾏う. これ
を繰り返し, 複数の分類器を得る.
– 予測時は, 個々の分類器の結果を並べたものを⼀つの符号とみなし, 適当な復号アルゴ
リズムを適⽤することで最終的な分類結果得る.
– 符号化（クラス集合の分割⽅法）を適切に設計することで、精度挙げられる.

26. 7.1.3 多クラスSVM
26
• 多クラス問題へのSVMの適⽤は未解決だが、実⽤上は1対他⽅式が最も広く
⽤いられている.
• 単⼀クラスSVM
– 確率密度分布の推定問題と関連した教師なし学習問題を解く⼿法.
– データの密度分布をモデル化する代わりに, ⾼確率でデータが観測される領域を囲む滑
らかな境界を求める⼿法.
– 境界は, その中でのデータが観測される確率が予め与えられた(0から1の間の)数値と等
しくなるように求められる.

27. 7.1.4 回帰のためのSVM
• 解の疎性を保ちながら、SVMを回帰問題に適⽤する.
• 線形回帰問題では、次の正則化された誤差関数を最⼩化したい.
• 疎な解を得るために、⼆乗誤差関数を ε許容誤差関数 (Vapnik, 1995)で置
き換える.
– 予測値y(x)と観測値tの差がε(>0)未満のときは, ε許容誤差関数の値は0になる.
• 誤差関数はこうなる：
27

28. 7.1.4 回帰のためのSVM
• 分類問題でのSVM同様, スラック変数を導⼊して最適化問題として表現.
– ２つのスラック変数 ξn>=0、𝜉" 𝑛>=0
– 図7.7のように ξn>0は tn>y(xn)+ε が成り⽴つデータ点に, 𝜉" 𝑛 > 0はtn<y(xn)-εが成り
⽴つデータ点に対応.
– 観測された値がεチューブの中に位置するという条件は, yn-ε<=tn<=yn+ε と等しい.
– 次のように⾮ゼロのスラック変数を導⼊することで, チューブの外側にデータ点が存在
することを許す制約条件かける.
• スラック変数⽤いてSVM回帰の誤差関数書き換える.
28

29. 7.1.4 回帰のためのSVM
• 誤差関数を ξn>=0、𝜉" 𝑛>=0および(7.53),(7.54)の制約下で最⼩化する.
– ラグランジュ乗数 an>=0, 𝑎'n>=0, μn>=0,𝜇'n>=0を⽤いて以下のラグランジュ関数の
停留点を求めることで解ける.
– y(x)を(7.1)で置き換え, w,b,ξn,𝜉" 𝑛に対する偏微分を0として以下を得る.
– これら⽤いて変形して、次の双対⽬的関数を{an}と{𝑎'n}について最適化する問題に帰
着.
29

30. 7.1.4 回帰のためのSVM
• (続き) 分類問題におけるSVMと同様に, 短形制約が成⽴し、これと(7.58)
が制約条件になる.
• (7.57)を(7.1)に代⼊して、新しい⼊⼒に対する予測値は以下のようにカー
ネル関数のみを⽤いて計算できることがわかる.
• SVM回帰のKKT条件（ラグランジュ乗数と対応する制約式の積が0という条
件）は、以下の式で与えられる.
– anが0以外の値を取る時：
• ε+ξn+yn-tn=0が成り⽴つ時 (対応するデータ点がεチューブの上側の境界上か, εチューブよ
り上にある時)
– 𝑎'n が0以外の値を取る時：
• 同様に、データ点がεチューブの下側の境界上か、それより下にある場合. 30

31. 7.1.4 回帰のためのSVM
• SVM回帰におけるサポートベクトルとは(7.64)による予測に寄与するデー
タ点のこと. ⾔い換えると, an≠0もしくは𝑎'n≠0が成⽴する点.
– εチューブ内部の点は全てan=𝑎'n=0が成⽴するのでサポートベクトルではない.
• SVM回帰でも通常のSVM同様に疎な解が得られ、予測値(7.64)を計算する
際はサポートベクトルのみ考慮すれば良いことがわかった.
• 正則化項のパタメータに対する直感的な解釈可能な定式化も
– 許容範囲の幅を決めるεを指定する代わりに、チューブの外側に存在するデータの割合
に対する上限γを指定し、⽬的関数を最⼤化する.
31

32. 7.1.5 計算論的学習理論
• SVMは計算論的学習理論/統計的学習理論という分野から⽣まれた.
• 計算論的学習理論は、PAC学習(Valiant(1984))から始まった.
– 良い汎化性能を達成するために、どれくらいの数の学習データが必要なのか明らかにし,
また, そこから学習にかかる計算時間の下限を計算することが⽬的.
– 具体的には、ある閾値よりも⾼い確率(high probablity)で、ある閾値よりも正しく
(approximately correct)予測を⾏う. この基準を満たすために最低限必要となるデータ
数Nを求めることを⽬的とする.
• PAC学習の導く下限はしばしば「最悪の場合における」ものと⾔われる.
– 訓練データとテストデータが同じ分布から独⽴に抽出されるという前提だが、実世界の
問題では分布に何らかの規則性が存在することが多い.
– そのため、実際の応⽤ではPAC学習理論から得られる下限が⽤いられることはあまりな
い.
32

33. 7.2 関連ベクトルマシン
• SVMにおける制限
– 出⼒は識別結果で、事後確率は計算できない.
– もともと2クラス分類のために作られていて、多クラス問題の拡張に問題多い
– 正則化パラメータCもしくはγ(回帰だとさらにε)は交差検定のようにホールドアウト
データを⽤いて決定する必要あり.
– 予測関数は訓練データを中⼼としたカーネル関数の線形組み合わせでなければならず,
そのカーネル関数も正定値のものに限られる.
• 関連ベクトルマシン(RVM)は回帰及び分類問題を解くために提案された疎な
カーネルベースのベイズ流学習⼿法.
– SVMの特性を引き継ぎながら、いろいろ問題点克服
– SVMよりさらに疎なモデル得られやすく、同等の汎化能⼒を持ちながら、より⾼速な予
測が可能に.
33

34. 7.2.1 回帰問題に対するRVM
• 3章で議論した線形モデルと同じ形式だが、疎な解が得られるように事前分
布に修正加える.
– 与えられた⼊⼒ベクトルxに対する実数値の⽬標変数tの条件付き確率分布を以下のよう
にモデル化.
– なお、平均値y(x)：
• RVMのモデルは、(7.77)をSVMと似た形に制限したもの. 具体的には基底
関数として個々の訓練データを⼀⽅の引数としたカーネル関数を⽤いて、以
下の形に制限する.
• SVMとの違い
– カーネル関数は正定値である必要ない
– 基底関数も、その数や中⼼が存在する位置が訓練データと関係ある必要ない.
• 尤度関数は次のようになる.
34

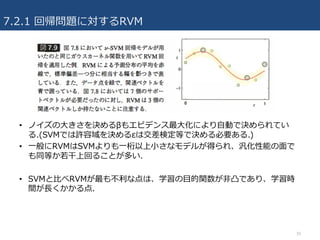
35. 7.2.1 回帰問題に対するRVM
• (続き) パラメータベクトルwの事前確率分布として、3章で⽤いた平均0の
ガウス事前分布を⽤いる. ただし, 超パラメータは個々のwiごとに異なるαi
を⽤いる.
– これらの超パラメータについてエビデンス最⼤化すると、⼤部分の超パラメータは無限
⼤になり、対応する重みパラメータの事後分布はゼロ⼀点に集中.
– → 対応する基底関数は予測において何の役割も果たさないため取り除け、疎なモデル
が得られる.
• 線形モデルに対する(3.49)の結果⽤いて, 重みベクトルに対する事後分布は
再びガウス分布となり, 次のように表される.
– Φは要素Φni=φi(xn)を持つNxMの計画⾏列. A=diag(αi).
35

36. 7.2.1 回帰問題に対するRVM
• α, βの値はエビデンス近似で求められる.
– まず重みパラメータについて積分
– 対数尤度
– (7.85)を超パラメータα,βに対して最⼤化することが⽬的.
• 3.5節のエビデンス近似のときと同様に対数尤度の微分を0と置いて,
• なお, γiは, 対応する重みパラメータwiが, データによりどれだけよく特定されたかを表す量
36

37. 7.2.1 回帰問題に対するRVM
• α, βの推定値を得る.
– まず適当にα,βの初期値を得て, (7.82), (7.83)から平均および共分散を計算する.
– それらを(7.87), (7.88)に代⼊し, (7.82), (7.83)から新たなαとβの推定値得る.
– この⼿順を適当な収束条件が満たされるまで繰り返す.
• 実際に最適化を⾏うと, 超パラメータ{αi}の⼀部は無限⼤になる.
– 対応する重みパラメータwiは平均・分散ともに0の事後分布を持つことになる.
– よって、これらのパラメータは対応する基底関数Φi(x)はモデルから取り除かれ、新し
い⼊⼒に対する予測に対して全く影響及ぼさなくなる.
• (7.78)の形のモデルの場合, ゼロでない重みを持つ基底関数に対応する⼊⼒
xnは関連ベクトル(relevance vector)と呼ばれる.
– これらの点は関連度⾃動決定によって得られ、SVMにおけるサポートベクトルと似た役
割
37

38. 7.2.1 回帰問題に対するRVM
• 尤度を最⼤化する超パラメータα*, β*が求まると, 新しい⼊⼒xに対する出
⼒tの確率分布を予測できる. (7.76)と(7.81)より,
• したがって, 予測値の平均は(7.76)で重みベクトルwを事後平均mとしたも
のに等しく、予測の分散は以下で表されるσ2(x)に等しい.
• ↑は線形回帰モデルにおける予測の分散と似ている. 3章での議論と同様に、
RVMのモデルも、データが存在しない領域で予測分散が⼩さくなるという
問題がある.
38

39. 7.2.1 回帰問題に対するRVM
• ノイズの⼤きさを決めるβもエビデンス最⼤化により⾃動で決められてい
る.(SVMでは許容域を決めるεは交差検定等で決める必要ある.)
• ⼀般にRVMはSVMよりも⼀桁以上⼩さなモデルが得られ、汎化性能の⾯で
も同等か若⼲上回ることが多い.
• SVMと⽐べRVMが最も不利な点は、学習の⽬的関数が⾮凸であり、学習時
間が⻑くかかる点.
39

40. 7.2.2 疎性の解析
• 関連度⾃動決定を⽤いると⼀部パラメータは０になり疎な解が得られる.
• RVMの場合について疎な解が⽣じる原因を詳しく調べる.
• また、その過程で、前の節で議論した超パラメータを直接⾼速化する⽅法よ
りも、はるかに⾼速に学習を⾏う⽅法に関して議論する.
40

41. 7.2.2 疎性の解析
• ベイズ線形モデル回帰モデルで疎な解が⽣じる原因について
– 訓練データN=2個, 出⼒はt1, t2,とする
– 基底関数がΦ(x), 重みに対応する超パラメータα, ノイズ精度β
– 周辺確率の尤度は, (7.85)より
– ただし共分散⾏列C：
• ⽬的：与えられた観測値tに対して、周辺尤度を最⼤化するα*, β*を求める.
– 図7.10より, φと訓練データベクトルtの⽅向に相関が低い場合, 超パラメータαは∞(重
み0)になり, 基底関数はモデルから取り除かれる.
– αが有限の値を持つようにすると, 訓練データの出⼒値を観測する確率が常に下がるため.
(実際, αが無限⼤でないと、確率分布は観測値から「離れる」⽅向に引き伸ばされ、観
測された出⼒値に対する確率が低下する.)
41

42. 7.2.3 分類問題に対するRVM
• 4章で議論した確率的な線形モデルに対して、7.2.2同様に関連度⾃動決定
を適⽤することで、RVMを分類問題に適⽤することができる.
• 以下, 2クラス問題に対応して2値の⽬標変数t∈{0,1}を出⼒するものとする.
• モデル：
– 基底関数の線形結合をロジスティックシグモイド関数で変換したもの.
– 個々の重みパラメータに対する精度超パラメータが別々である点が、4章でのモデルと
は異なる.
• 回帰モデルの場合と異なり, 分類モデルではwについて解析的に積分できな
いので、ラプラス近似を⾏う(4.4節)
– まず, 超パラメータのα初期化.
– 次に, 今のαの値に対して, 事後分布をガウス分布で近似し, その近似分布を⽤いて周辺
化尤度を計算.
– 最後に, 得られた近似周辺化尤度を最⼤化するようにαを更新する.
– このステップを適当な収束条件が満たされるまで続ける.
42

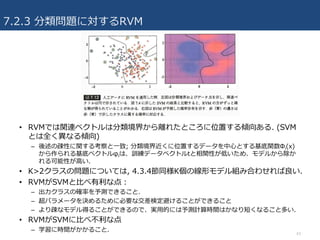
43. 7.2.3 分類問題に対するRVM
• RVMでは関連ベクトルは分類境界から離れたところに位置する傾向ある. (SVM
とは全く異なる傾向)
– 後述の疎性に関する考察と⼀致; 分類境界近くに位置するデータを中⼼とする基底関数Φi(x)
から作られる基底ベクトルφiは、訓練データベクトルtと相関性が低いため、モデルから除か
れる可能性が⾼い.
• K>2クラスの問題については, 4.3.4節同様K個の線形モデル組み合わせれば良い.
• RVMがSVMと⽐べ有利な点：
– 出⼒クラスの確率を予測できること.
– 超パラメータを決めるために必要な交差検定避けることができること
– より疎なモデル得ることができるので、実⽤的には予測計算時間はかなり短くなること多い.
• RVMがSVMに⽐べ不利な点
– 学習に時間がかかること.
43

44. 7.2.2 疎性の解析 数学的な解釈 補⾜
44
• 以下の２つの量を導⼊してる
– si：φiの疎性パラメータ
• 基底ベクトルφiが他の基底ベクトルとどれだけ重複しているかの⽬安.
– qi：φiの品質パラメータ
• 基底ベクトルφiと、誤差ベクトル（訓練データの観測値tとベクトルφiを取り除いたモデルに
よる予測値y-iの差）にどれだけ相関があるか.
• siがqiより⼤きな基底関数φiはモデルから取り除かれる可能性が⾼い.

45. 参考資料
• パターン認識と機械学習 下 (ベイズ理論による統計的予測)
– C.M. ビショップ (著), 元⽥ 浩 (監訳), 栗⽥ 多喜夫 (監訳), 樋⼝ 知之 (監訳), 松本 裕
治 (監訳), 村⽥ 昇 (監訳)
• PRML chapter7 （Takahiro (Poly) Horikawa, SlideShare）
– https://www.slideshare.net/thorikawa/prml-chapter7
• Prml07 （Tsukasa Fukunaga, SlideShare）
– https://www.slideshare.net/tsukasafukunaga5/prml07-17444396
45