More Related Content
PPTX
PDF
PDF
PDF
PPTX
PPTX
ベイズ深層学習5章 ニューラルネットワークのベイズ推論 Bayesian deep learning PDF
PDF
[DL輪読会]Control as Inferenceと発展 What's hot
PDF
PPTX
【DL輪読会】言語以外でのTransformerのまとめ (ViT, Perceiver, Frozen Pretrained Transformer etc) PDF
SSII2021 [OS2-01] 転移学習の基礎:異なるタスクの知識を利用するための機械学習の方法 PDF
PDF
PPTX
勾配ブースティングの基礎と最新の動向 (MIRU2020 Tutorial) PDF
PPTX
PDF
PDF
PDF
PPTX
PPTX
[DL輪読会]When Does Label Smoothing Help? PDF
PPTX
PPTX
Sliced Wasserstein距離と生成モデル PDF
PDF
PDF
Bayes Independence Test - HSIC と性能を比較する- PPTX
マルコフ連鎖モンテカルロ法 (2/3はベイズ推定の話) Viewers also liked
PDF
PDF
PPTX
PDF
Complement Naive Bayesによるワードの自動カテゴリ分類 PDF
"Estimating Tree-Structured Covariance Matrices via Mixed-Integer Programming" PPTX
PDF
PDF
PDF
Similar to グラフィカルモデル入門
PDF
PDF
PPTX
【機械学習プロフェッショナルシリーズ】グラフィカルモデル1章 PPTX
PPTX
【機械学習プロフェッショナルシリーズ】グラフィカルモデル2章 PDF
PDF
PPTX
PDF
Probabilistic Graphical Models 輪読会 #1 PDF
PDF
Infer net wk77_110613-1523 PDF
Graphical modellab concept_ja PPTX
SSII2020SS: グラフデータでも深層学習 〜 Graph Neural Networks 入門 〜 PDF
PDF
PPTX
DiagrammeRと仲良くなった話ーグラフィカルモデルのためのDiagrammeR速習ー PDF
PDF
[DL輪読会]Relational inductive biases, deep learning, and graph networks PDF
StanとRでベイズ統計モデリング読書会 導入編(1章~3章) PDF
YOU は何して VLDB2020 Tokyo へ? (グラフ編) グラフィカルモデル入門
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
- 34.
- 35.
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
- 56.
- 57.
- 58.
- 59.
- 60.
- 61.
- 62.
- 63.
- 64.
- 65.
- 66.
- 67.
参考文献
機械学習・パターン認識・コンピュータビジョン全般
*すべて,あるいは一部の原稿が著者webページからダウンロード可のものをリストアップ
・C.M.Bishop,Pattern Recognition andMachine Learning, Springer, 2006
邦訳:パターン認識と機械学習 (上・下),丸善,2012
・D.Barber, Bayesian reasoning and machine learning, Cambridge University Press, 2012
・R.Szeliski, Computer Vision: Algorithms and Applications, Springer, 2011
邦訳:コンピュータビジョン ―アルゴリズムと応用―,共立出版,2013
・S.J.D.Prince, Computer Vision: models, learning and inferance, Cambridge University Press, 2012
ビデオレクチャ
*最近では,YouTube等で「graphical model」と検索すれば多くの(そして有名人の)ビデオレクチャが
見られます.例えば,MOOCsの代表格であるCourseraでは「Probabilistic Graphical Models」がDaphne
Koller教授より提供されている(この人は有名なテキスト「Probabilistic Graphical Models,MIT Press,
2009」の 著者でもあり,Courseraの設立者でもあります). 日本語では,玉木先生(広島大)によるレク
チャがUdamyで公開されてます.
ソフトウェア
マルコフ確率場:新しいアルゴリズムが実装されているという意味ではOpenGMがよいかも.
ベイジアンネットワーク:HMMの実装はあちらこちらにある.
また,グラフを自動的に描きたいときは,Graphvizというソフトウェアがある.

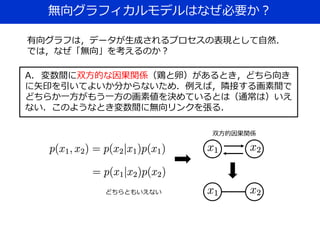
![グラフィカルモデルとは?
グラフィカルモデル
= 確率変数間の依存関係のグラフ表現
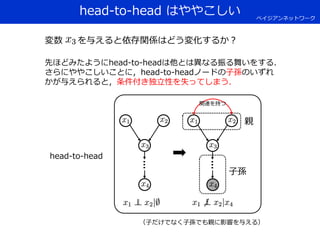
例:確率変数 の間に左のような依存関係が存在
・近年の機械学習やコンピュータビジョンでの定番モデル
(実際,2000年以降に出版されたおもだった機械学習やコンピュータ
ビジョンの教科書にはグラフィカルモデルの説明がある)
[Bishop,2006][Szeliski,2011][Prince,2012] etc.](https://image.slidesharecdn.com/graphicalmodel-140604101314-phpapp01/85/slide-2-320.jpg)
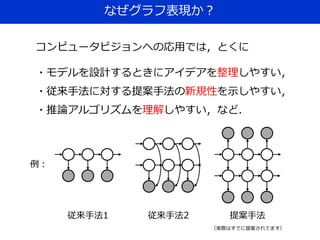
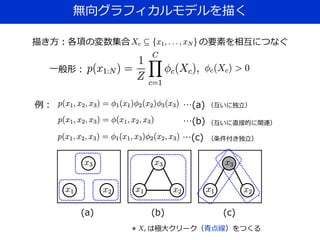
![なぜグラフ表現か?
1)確率モデルの構造を視覚化する簡単な方法を提供し,
新しいモデルの設計方針を決めるのに役に立つ.
2)グラフの構造を調べることにより,条件付き独立性
などのモデルの性質に関する知見が得られる.
3)精巧なモデルにおいて推論や学習を実行するために
は複雑な計算が必要となるが,これを数学的な表現を暗
に伴うグラフ上の操作として表現することができる.
[Bishop,2006 第8章(邦訳:パターン認識と機械学習 (下),丸善,2012 )]](https://image.slidesharecdn.com/graphicalmodel-140604101314-phpapp01/85/slide-3-320.jpg)