Download as PDF, PPTX
![[DL輪読会]Control as Inferenceと発展](https://cdn.slidesharecdn.com/ss_thumbnails/20191004-191204055019-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]Wasserstein GAN/Towards Principled Methods for Training Generative Adv...](https://cdn.slidesharecdn.com/ss_thumbnails/wgan-1-170224021826-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]相互情報量最大化による表現学習](https://cdn.slidesharecdn.com/ss_thumbnails/20190913iwasawa-190913002312-thumbnail.jpg?width=640&height=640&fit=bounds)
PRML輪読#13
- 1.
- 2. 構成 13.1 マルコフモデル 13.2 隠れマルコフモデル 13.3線形動的システム 2
- 3. はじめに • 前章までの議論：独⽴同分布に従うデータ点の集合に関する議論 – 各データ点における確率分布の積によって尤度関数を表現できた •本章の議論：独⽴同分布の仮定が当てはまらない場合の議論 – その重要な例：系列データ • 定常 ：データを⽣成する分布⾃体は常に同じ（本章ではこちらを扱う） • ⾮定常：データを⽣成する分布⾃体も変化する • 時系列データの扱い⽅ – 未来の予測が過去の全ての観測値に広く依存している？ → 際限なく複雑に – 直近の観測値以外の過去の観測値に対し独⽴と仮定 → マルコフモデル • メリット：扱いやすい • デメリット：制限が強い • 潜在変数を導⼊することで扱いやすさを保ちながらより⼀般的な枠組みへ→状態空間モデル 3
- 4. 13.1 マルコフモデル • 系列データを扱う最も簡単な⽅法 –系列の性質を無視して独⽴同分布に従うものと仮定して扱う – 順序に関係するパターンを捉えられない • 独⽴同分布の仮定を緩める → マルコフモデルで考える – 観測系列の同時分布 – 最も近い観測値以外のすべての過去の観測値から独⽴と仮定（⼀次マルコフ連鎖） 4
- 5. 13.1 マルコフモデル • 独⽴同分布の仮定を緩める→ マルコフモデルで考える – 均⼀マルコフ連鎖：条件付き分布が皆同⼀であるという制約(定常時系列) • 例）条件付き分布がパラメトリックなら、すべての条件付き分布のパラメータが同じ – M次マルコフ連鎖：過去のM個の観測値以外のすべての過去の観測値から独⽴と仮定 • 柔軟性がます⼤⼩にモデルのパラメータ数が KM(K-1) と指数的に増加 (Kは状態数) • 連続変数の場合 – ⾃⼰回帰モデル • 各ノードが平均が親ノードの線形関数となるガウス分布を持つ – ニューラルネットワーク（タップ付き遅延線） 5
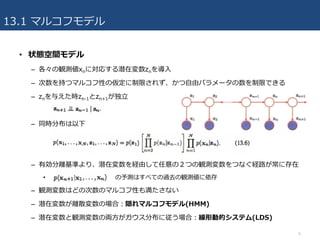
- 6. 13.1 マルコフモデル • 状態空間モデル –各々の観測値xnに対応する潜在変数znを導⼊ – 次数を持つマルコフ性の仮定に制限されず、かつ⾃由パラメータの数を制限できる – znを与えた時zn-1とzn+1が独⽴ – 同時分布は以下 – 有効分離基準より、潜在変数を経由して任意の２つの観測変数をつなぐ経路が常に存在 • の予測はすべての過去の観測値に依存 – 観測変数はどの次数のマルコフ性も満たさない – 潜在変数が離散変数の場合：隠れマルコフモデル(HMM) – 潜在変数と観測変数の両⽅がガウス分布に従う場合：線形動的システム(LDS) 6
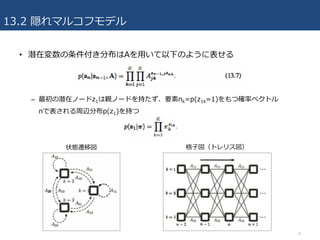
- 7. 13.2 隠れマルコフモデル • 状態空間モデルにおいて、潜在変数が離散変数である特別な例 –ある⼀つの時刻について⾒ると、成分密度分布がp(x|z)で与えられる混合分布 – 各観測での混合成分が、独⽴に選択されるのではなく、過去の観測で選択された 成分に依存して選択されるように混合分布モデルを拡張したものと解釈可能 – 利⽤例：⾳声認識、⾃然⾔語モデル、御来⼿書き⽂字認識、⽣物学的配列の解析 • 潜在変数は離散的な多項変数zn – どの混合成分が対応する観測xnを⽣成するかを記述(1-of-K表現) – znの確率分布はzn-1に依存し、潜在変数はK次元の⼆値変数なので、条件付き分布 p(zn|zn-1)は遷移確率を要素に持つ数表Aに対応する – AはK(K-1)個の独⽴なパラメータをもつ 7
- 8. 13.2 隠れマルコフモデル • 潜在変数の条件付き分布はAを⽤いて以下のように表せる –最初の潜在ノードz1は親ノードを持たず、要素πk=p(z1k=1)をもつ確率ベクトル πで表される周辺分布p(z1)を持つ 8 状態遷移図 格⼦図（トレリス図）
- 9. 13.2 隠れマルコフモデル • 観測変数の条件付き確率分布p(xn|zn,φ)：出⼒確率 – xが連続的な場合はガウス分布(9.11) – xが離散的な場合は条件付き確率表 – xnは観測されるので、φが与えられた時p(xn|zn, φ)は⼆値ベクトルznのK状態に対応す る、要素数Kのベクトル • 均⼀なモデル – 潜在変数を⽀配するすべての条件付き分布が同じパラメータAを共有 – すべての出⼒分布が同⼀のパラメータφを共有 – 潜在変数と観測変数の同時確率分布は以下 9
- 10. 13.2 隠れマルコフモデル • ⽣成モデルの観点から整理する –最初の潜在変数z1をパラメータπkで⽀配される確率で選択 – 対応する観測値x1を抽出 – z1の既に実現化された値を⽤いて遷移確率p(z2|z1)に従って変数z2の状態を選択 – 対応する観測値x2を抽出... 10
- 11. 13.2 隠れマルコフモデル • HMMの遷移確率Aの形に制限を加えることでさまざまな変異形を得る •例：left-to-right HMM – Aのk<jとなるAjk=0 – k>j+ΔならAjk=0(状態インデックスの⼤きな変化を避ける) • ⾳声認識やオンライン⼿書き⽂字認識ではleft-to-right HMM を採⽤ – p.332 11
- 12. 13.2.1 HMMの最尤推定 • 同時分布(13.10)を潜在変数について周辺化して尤度関数(13.11)を得る •同時分布・尤度関数の計算 – nについて分解できないのでznに関する和を独⽴には扱えない – 和をとる対象が各々K個の状態を持つN個の変数なので、和演算を明⽰的には⾏えない – 混合分布の⼀般化に相当し、尤度関数を直接最⼤化しようとすると閉じた解を持たない • i.i.dに従うデータに対する混合モデルはHMMの特殊な場合 12 →EMアルゴリズムで効率的に尤度最⼤化
- 13. 13.2.1 HMMの最尤推定 • EMアルゴリズム –最初にモデルパラメータをある初期集合に設定 θold – Eステップ（ ⽬的：γ(zn), ξ(zn-1, zn)を効率的に求める） • θoldから潜在変数p(Z|X, θold)の事後分布を求める • p(Z|X, θold)から完全データに対する尤度関数の対数の期待値Qを求める • γ(zn), ξ(zn-1, zn)を導⼊ 13
- 14. 13.2.1 HMMの最尤推定 • EMアルゴリズム –Mステップ • γ(zn), ξ(zn-1, zn)を定数と⾒なし、パラメータ に関してQ(θ, θold)を最⼤化 • πとAに関する最⼤化はラグランジュ乗数を⽤いて求まる • πとAの要素のうち、初期値がゼロのものはその後の更新においてもゼロのまま。初期化にお いては、パラメータの初期値として和や⾮負の制約を満たすランダムな値を選択。 14
- 15. 13.2.1 HMMの最尤推定 • EMアルゴリズム –Mステップ – EMアルゴリズムでは出⼒分布のパラメータの初期値が必要なので、はじめはデータがi.i.dに 従うと仮定して最尤推定を⾏い、そこで得られた値をEMにおける初期値とすることがある。 15
- 16. 13.2.2 フォワード＿バックワードアルゴリズム • EMアルゴリズムのEステップに対応するγとξを求める効率的な⽅法 •HMMのグラフは⽊構造を持ち、２段階のメッセージパッシングアルゴリズ ムで潜在変数の事後確率が効率よく求められる – 本節：確率の加法・乗法定理、有効分離に基づく条件付き独⽴を⽤いた導出 – 次節：積和アルゴリズムの特殊な例として簡単に得られることを確認 16
- 17. 13.2.2 フォワード＿バックワードアルゴリズム • 導出の流れ(詳細はp.336-343を参照) –γ(znk)を求める – ξ(zn-1, zn)を求める 17
- 18. 13.2.2 フォワード＿バックワードアルゴリズム • EMアルゴリズムを⽤いたHMMの学習に必要な過程についてのまとめ –最初にパラメータθoldの初期値を定める – フォワードα再帰とバックワードβ再帰によってγ(zn)とξ(zn, zn-1)を求める • この段階で尤度関数も求めることができる – 以上でEステップが完了し、その結果からMステップの式によってパラメータθを更新 – ある収束基準が満たされるまでEステップとMステップを交互に繰り返す • 予測分布 – データXが観測された時のxn+1の予測 – x1からxNまでのすべてのデータの影響が α(zN)のKの値にまとめられている ＝少量の記憶領域で無限の未来まで計算可能 18
- 19. 13.2.3 HMMの積和アルゴリズム • HMMのグラフは⽊構造 –隠れ変数の局所的な周辺分布を求める問題を積和アルゴリズムで解くことができる – 当然、フォワード＿バックワードアルゴリズムと同⼀の結果 • 導出の流れ – 図13.5の有向グラフを因⼦グラフに変換 – 出⼒確率を遷移確率因⼦に吸収して因⼦グラフを単純化 – α再帰とβ再帰を求める – 周辺確率を求める 19
- 20. 13.2.4 スケーリング係数 • フォワード＿バックワードアルゴリズムを利⽤する前に議論すべき問題 –再帰式(13.36)において、各ステップの新しい値 – アンダーフローを起こしやすいが、i.i.dに従うデータのように対数尤度を計算すること はできない • ⼩さい数同⼠の積の和をとっているから – αとβを１のオーダーに収まるようにスケーリング – p.346-347 20
- 21. 13.2.5 Viterbiアルゴリズム • 潜在変数の意味解釈 –与えられた観測系列に対し、隠れ状態の最も確からしい系列は？ – 例：⾳声認識、観測⾳響データ系列から最も確からしい⾳素系列を⾒つけたい • Viterbiアルゴリズムというmax-simアルゴリズムで解く – 格⼦図中の可能な経路の数が鎖の⻑さに対し指数的に増加 – Viterbiアルゴリズムは、この経路空間を効率的に探索し、鎖の⻑さに対したかだか線形 に増加する計算量で最も確からしい系列を⾒つける 21
- 22. 13.2.5 Viterbiアルゴリズム • 導出の詳細な流れはp.348を参照 –基本的には積和アルゴリズム同様、HMMを因⼦グラフで表現し伝播されるメッセージ を計算し、最も確からしい経路に対応する同時分布p(X,Z)を求め、この経路に対応する 潜在変数の値の列も⾒つける • 直感的な理解 – 格⼦図中の指数的に増える経路探索の計算量をいかに削減するか？ – 各々の経路について格⼦図の中を進み、遷移確率と出⼒確率の積を⾜し上げていってそ の経路の確率を計算 – ある時刻ステップnにおける状態Kに対応するノードに集まる経路の内最⼤の確率のもの のみ記録→K個を記録 – 最後の時刻ステップNに到達した時、その状態に⼊ってくる経路は⼀つだけなので経路 を戻っていき、その経路の状態を確認していく 22
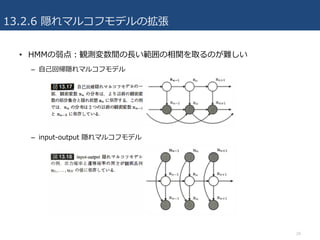
- 23. 13.2.6 隠れマルコフモデルの拡張 • HMMx 識別学習 – HMMは⽣成モデルとしては貧弱 – 分類⽬的なら、最尤推定よりも識別学習でHMMのパラメータを決定したほうが良い – R個の観測系列の訓練集合Xrとそれぞれにクラスmがラベルづけ – 各クラスに対し別々にパラメータθmを持つHMMを⽤意して、そのパラメータを以下の 交差エントロピー最適化によって決定 • HMMの弱点 – システムがある与えられた状態に留まる時間の分布を現実的な形で表現できない – 観測変数間の⻑い範囲の相関を取るのが難しい 23 ＝
- 24. 13.2.6 隠れマルコフモデルの拡張 • HMMの弱点：観測変数間の⻑い範囲の相関を取るのが難しい –⾃⼰回帰隠れマルコフモデル – input-output 隠れマルコフモデル 24
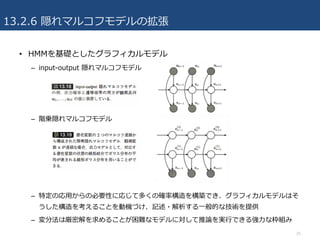
- 25. • HMMを基礎としたグラフィカルモデル – input-output隠れマルコフモデル – 階乗隠れマルコフモデル – 特定の応⽤からの必要性に応じて多くの確率構造を構築でき、グラフィカルモデルはそ うした構造を考えることを動機づけ、記述・解析する⼀般的な技術を提供 – 変分法は厳密解を求めることが困難なモデルに対して推論を実⾏できる強⼒な枠組み 13.2.6 隠れマルコフモデルの拡張 25
- 26. 13.3 線形動的システム • 線形動的システム(LDS) –潜在変数が連続変数の場合 – 必要条件：鎖の⻑さに対して線形の効率的な推論アルゴリズムを得る – xnもznもグラフ上の親ノードの状態の線形関数によって平均が表される多次元ガウス分 布に従う、線形ガウス状態空間モデルについて考察する • HMM：連続した観測値の相関を許した、混合モデル(9章)の拡張 • LDS：連続潜在変数モデル(12章)の⼀般化 – ノードの組{xn,zn}が、ある特定の観測に対する線形ガウス分布の潜在変数モデル – {zn}は独⽴ではなく、マルコフ連鎖を形成している – すべての変数の同時確率や周辺確率、条件付き確率などはガウス分布 • ここに最も確からしい潜在変数の値の系列は、最も確からしい潜在系列と同じ • Viterbiアルゴリズムのようなものを考えなくていい 26
- 27. 13.3 線形動的システム • 遷移確率分布 •出⼒確率分布 • 最初の潜在変数 • 以下の等価な式で表現されることが⼀般的 • モデルパラメータはEMアルゴリズムによる最尤推定で決定できる 27
- 28. 13.3.1 LDSにおける推論 • 以下を推論 –観測系列で条件付けられた潜在変数の周辺分布 – 与えられたパラメータ設定に対して観測データによって条件付けられた、次の時刻の潜 在状態znと観測変数xn • 潜在変数についての我が積分に置き換えられる点以外はHMMと同じ – p.356-360 28
- 29. 13.3.2 LDSの学習 • ここまでのLDSの推論問題の考察 –モデルパラメータ は既知と仮定 – 最尤推定を⽤いてこれらのパラメータを推定する – モデルが潜在変数を持つのでEMアルゴリズムで議論 • EMアルゴリズムの導出 – 完全データの尤度関数 – 事後分布p(Z|X, θold)について完全データ尤度関数の期待値を取る • Mステップではθの成分についてこの関数を最⼤化 29
- 30.
- 31.
- 32.
- 33. 13.3.3 LDSの拡張 • LDSにおける線形ガウスモデルの仮定 –推論と学習の効率的なアルゴリズムを導ける – ⼀⽅、観測変数の周辺分布が単なるガウス分布であるという⼤きな制約でもある • 線形ガウス分布以外の遷移確率分布や出⼒確率分布を導⼊すると推論は困難 – 多くの応⽤では単純なガウス出⼒密度による近似は粗すぎる – ⼀⽅、混合ガウス分布を出⼒密度に使おうとすると指数的に成分が増加する – 決定論的な近似や次節のサンプリング⼿法が利⽤できる – よく使われる⼿法：予測分布の平均付近を線形化することでガウス分布近似を⾏う拡張 カルマンフィルタ 33
- 34. 13.3.4 粒⼦フィルタ • 線形ガウスモデルでない動的システムではサンプリング(11章)を⽤いる –11.1.5節のSIR(Sampling-Importance-Resampling)の定式化を⽤いると、粒⼦フィ ルタとして知られる逐次モンテカルロアルゴリズムを得る • 粒⼦フィルタのアルゴリズムの各ステップは２つの段階からなる 34
- 35. 参考⽂献 • パターン認識と機械学習 下 –C.M. ビショップ (著), 元⽥ 浩 (監訳), 栗⽥ 多喜夫 (監訳), 樋⼝ 知之 (監訳), 松本 裕治 (監訳), 村⽥ 昇 (監訳) 35