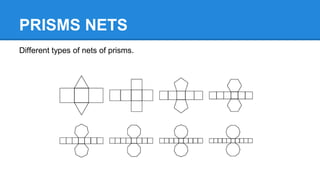
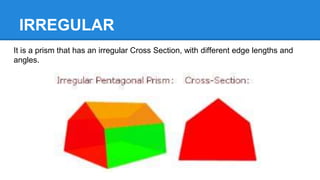
A prism is a solid geometric shape with identical cross-sectional areas and two faces that are identical, parallel polygons. There are different types of prisms including triangular, rectangular, pentagonal, and hexagonal prisms. To solve prisms, you calculate the surface area as 2 times the area of the base plus the perimeter of the base times the height, and the volume as the area of the base times the height. Prisms can also be regular, irregular, right, or oblique depending on the shape of their cross-sections and angles. The document provides examples of calculating surface areas and volumes of various prisms.

1. PRISMS
By: Lim Zia Huei, Ee Yun Shan, Nabila Hanim, Zoe, Afiqah
Zariful, Kodaruth humairaa

2. WHAT ARE PRISMS?
● A solid object with identical ends.
● Has flat sides (no curves)
● Has a cross section.

3. HOW TO SOLVE PRISMS?
To solve prism we have to:
● Find out the surface area
(2 X Area of base + perimeter of base X H)
● Volume of the prism
● Area & Volume of Cross Section

4. TYPES OF PRISMS
● Triangular
● Rectangular
● Pentagonal Prism
● Hexagonal Prism

5. PRISMS NETS
Different types of nets of prisms.

6. REGULAR
It is a prism that has a regular Cross Section, with equal edge lengths and
equal angles.

7. IRREGULAR
It is a prism that has an irregular Cross Section, with different edge lengths and
angles.

8. RIGHT VS OBLIQUE PRISMS
Right Prism: It is a geometric solid that has a polygon as its base and vertical
sides perpendicular to the base.
Oblique Prism: The joining edges and faces are not perpendicular to the base
faces.

9. SURFACE AREA
b = area of a base
p = perimeter of a base
h = height of the prism
Surface Area
= 2(½ X 8 X 3) + [(8+5+5) X 12]
= 240 cm2
Area = 2b + ph

10. VOLUME
b = area of base
h = height
Example:
Volume = (½ X 8 X 3) X 12
= 144 cm3
Volume = bh

11. EXAMPLE:
Area of cross-section
= (7x12) - (3x4)
= 84 - 12
= 72 m2
Volume of prism
= 72 x 5
= 360 m3
The diagram shows a cross-section of a cuboid after a cube is cut
out from it.

12. EXAMPLE:
Finding the volume of the oblique prism.
Volume of the oblique prism
= [ ½ x (8+4) x 9 ] x 15
= 54 x 15
= 810 cm2