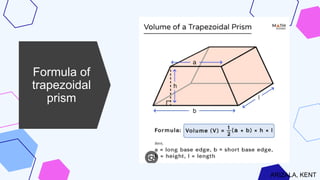
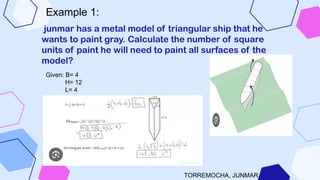
The document discusses the triangular and trapezoidal prisms, covering their definitions, historical significance, and applications in architecture and engineering. It explains how to calculate their volume and surface area, illustrated with example problems. The contributions of ancient mathematicians like Euclid and the impact of calculus on the understanding of these shapes are also highlighted.

1. PRISM (TRIANGULAR
AND TRAPEZIODAL)
GROUP 4
EDP CODE: 51946
MEMBERS:
CARAMBACAN, FRANCIS KYLE
ARIZALA, KENT JG
DELA TORRE, JERALD T.
MARFIL, KEN
SUMAYA, RHEDTNE BRYCE
HILIS, RJ V.
TORREMOCHA, JUMMAR

2. OBJECTIVE OF
PRISM
(TRIANGULAR
AND
TRAPEZOIDAL

3. At the end of this report the students should be able to:
• What is the History of Prism (Triangular and Trapezoidal)
• Define Prism (Triangular and Trapezoidal)
• Explain the Importance Prism (Triangular and Trapezoidal)
- Importance application of Triangular Prism and Trapezoidal
Prism
- How to calculate the Volume and Surface area of Triangular
Prism
- How to calculate the Volume and Surface area of Trapezoidal
Prism
Objectives:
I. OBJECTIVES
CARAMBACAN,
FRANCIS KYLE

4. HISTORY OF
TRIANGULAR AND
TRAPEZOIDAL PRISM

5. HISTORY
TRIANGULAR PRISM
• In geometry, a triangular prism or trigonal prism!" is a prism with 2
triangular bases. If the edges pair with each triangle's vertex and if they
are perpendicular to the base, it is a right triangular prism. A right
triangular prism may be both semiregular and uniform.
.
The triangular prism can be used in constructing
another polyhedron. Examples are some of the
Johnson solids, the truncated right triangular prism,
and Schönhardt polyhedron.
-The triangular prism, with two triangular bases and
three rectangular faces, dates back to ancient
geometry, notably referenced by Euclid in his
Elements (circa 300 BCE). The Renaissance
increased interest in geometric studies, and the
17th-century calculus further explored its
properties. Today, triangular prisms are important
in architecture, optics, and engineering for their
structural and refractive qualities.
SUMAYA RHEDTNE BRYCE

6. HISTORY
• The trapezoidal prism, with two
parallel trapezoidal bases and
rectangular sides, has origins in
ancient geometry. Its principles can
be traced back to Euclid's Elements
(circa 300 BCE), which influenced the
study of prisms. The development of
calculus in the 17th century
expanded understanding of their
volume and surface area. Today,
trapezoidal prisms are used in
architecture, engineering, and
computer graphics for modeling and
design.
l
DELA TORRE, JERALD
TRAPEZOIDAL PRISM

7. HISTORY
DELA TORRE AND
SUMAYA
Fuclid was the most prominent mathematician of Greco-
Roman antiquity, best known for his treatise on
geometry, the Elements.
"Ancient Civilizations"
Ancient civilizations like Egyptians, Babylonians,
and Greeks made important advanced geometry
through architectural feats, surveying methods,
and mathematical breakthroughs, laying the
groundwork for geometric principles.
"Euclidean Geometry"
Euclid, a Greek mathematician, formalized
geometry in his work "Elements" around 300
BCE, providing a systematic approach to
understanding geometric shapes and properties.

8. CARAMBACAN,
FRANCIS KYLE
DEFINITION OF
TRIANGULAR
AND TRAPEZOIDAL
PRISM

9. TRAINGULAR PRISM
- Triangular Prism is a pentahedron and has nine distinct nets. The edges and
vertices of the bases are joined with each other via three rectangular sides.
The sides of the triangular prism, which are rectangular in shape are joint
with each other side by side. All cross-sections parallel to the base faces are
the same as a triangle. A triangular pyramid has four triangular bases unlike
the triangular prism, joined with each other and all are congruent to each
other.
CARAMBACAN,
FRANCIS KYLE
CARAMBACAN,
FRACIS KYLE

10. TRAPEZOIDAL PRISM
- A trapezoidal prism is a prism with the base of a trapezoid.
There are six sides in a trapezoidal prism, four of those sides
are rectangles, and they form the height of the prism. The
bases, or the top and bottom of the prism, are congruent
trapezoids which is why it is called a trapezoidal prism.
CARAMBACAN,
FRANCIS KYLE

11. Formula of triangular prism
ARIZALA, KENT

12. See the example below to see how to find the volume
of a triangular prism!
ARIZALA, KENT

13. Here's Surface Area Formula:
Example:
ARIZALA, KENT

14. Formula of
trapezoidal
prism
ARIZALA, KENT

15. ARIZALA, KENT

16. Problem Solving
Or Statement
For triangular
and trapezoidal

17. Example 1:
junmar has a metal model of triangular ship that he
wants to paint gray. Calculate the number of square
units of paint he will need to paint all surfaces of the
model?.
Given: B= 4
H= 12
L= 4
TORREMOCHA, JUNMAR

18. Example Problem 2: Consider a ship with length
100 m and a V-shaped cross section shown below
where 0 = 35°. If the boat is in static equilibrium
when the water reaches a height h, = 8 m, what is
the ship's mass?
Given: l =100m
H= 8m
θ=35
TORREMOCHA, JUNMAR

19. Example1:
Given:
base area: 361m2
Length: 12.5m
MARFIL, KEN

20. Example 2: Find the lateral surface area of an isosceles
SHIP trapezoidal prism with parallel edges of the base
6 cm and 12 cm, the legs of the base 5 cm each, the
altitude of the base 4 cm, and height of the prism 10
cm.
MARFIL, KEN

21. CONCLUSION
HILIS, RJ

22. V. REFERENCES
• https://www.cuemath.com/geometry/triangular-prism/
• https://en.wikipedia.org/wiki/Triangular_prism/
• https://www.cuemath.com/geometry/trapezoidal-prism/
• https://mathmonks.com/prism/trapezoidal-prism
• https://thirdspacelearning.com/gcse-maths/geometry-and-measure/surface-area-of-a-
triangular-prism/
REFERENCES
HILIS, RJ

23. THAT’S ALL,
THANK YOU!