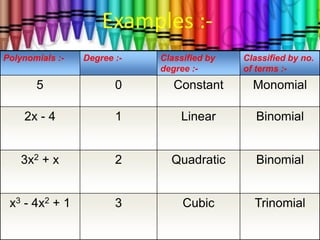
The document discusses key concepts related to polynomials including: - Constants and variables are the building blocks of polynomials, with constants having fixed values and variables able to take on different values. - A polynomial is an algebraic expression with variables that have only non-negative integral powers. - Polynomials are classified based on degree, with the highest power of a variable determining the degree, and also classified based on the number of terms. - Important concepts include the remainder and factor theorems, which relate the remainder and factors of a polynomial to its value when a variable is substituted.

1. Subject :- Maths
Topic :- Polynomials
Made by :-
Nirav Vaishnav.

2. Constants : A symbol having a fixed numerical value is called a
constant.
Eg :- In polynomial 3x + 4y ,3 and 4 are the constants.
Variables : A symbol which may be assigned different numerical
values is called as a variables.
 Eg :- In polynomial 3x + 4y , x and y are the variables.
Algebraic Expression : The combination of constants and variables are
called algebraic expressions.
Eg :- 2x3–4x2+6x–3 is a polynomial in one variable x.
4+7x4/5+9x5 is an expression but not a polynomial since it contains a
term x4/5, where 4/5 is not a non-negative integer.
Polynomials : An algebraic expression in which the variable involved
have only non –negative integral powers is called a polynomial.
Important Terms :-

3. Degree : The highest power of a variable in the polynomial is
called degree of that polynomial.
Eg. : 5x2 + 3 , here the degree is 2.
Constant polynomial : A polynomial containing one term only ,
consisting of a constant is called a constant polynomial.
The degree of a non-zero constant polynomial is zero.
Eg. : 3 , -5 , 7/8 , etc. , are all constant polynomials.
Zero polynomial : A polynomial consisting one term only ,
namely zero only , is called a zero polynomial.
The degree of a zero polynomial is not defined.
Continued...

4. Types of polynomial (on the basis of terms) :-
Monomial : Algebric expression that consists
only one term is called monomial.
Binomial : Algebric expression that consists
two terms is called binomial.
Trinomial : Algebric expression that consists
three terms is called trinomial.

5. Types of polynomial (on the basis of degree) :-
Linear polynomial: A polynomial of degree 1 is called a
linear polynomial.
Quadratic polynomial: A polynomial of degree 2 is called a
quadratic polynomial.
Cubic polynomial : A polynomial of degree 3 is called a
cubic polynomial.
Biquadratic polynomial : A polynomial of degree 4 is called
a biquadratic polynomial.

6. Examples :-
Polynomials :- Degree :- Classified by
degree :-
Classified by no.
of terms :-
5 0 Constant Monomial
2x - 4 1 Linear Binomial
3x2 + x 2 Quadratic Binomial
x3 - 4x2 + 1 3 Cubic Trinomial

7. Remainder Theorem :-
Let f(x) be a polynomial of degree n > 1 and let a be any real number.
When f(x) is divided by (x-a) , then the remainder is f(a).
PROOF :- Suppose when f(x) is divided by (x-a), the quotient is g(x) and the
remainder is r(x).
Then, degree r(x) < degree (x-a)
 degree r(x) < 1 [ therefore, degree (x-a)=1]
degree r(x) = 0
r(x) is constant, equal to r (say)
Thus, when f(x) is divided by (x-a), then the quotient is g9x) and the remainder is r.
Therefore, f(x) = (x-a)*g(x) + r (i)
Putting x=a in (i), we get r = f(a)
Thus, when f(x) is divided by (x-a), then the remainder is f(a).

8. Factor Theorem :-
Let p(x) be a polynomial of degree n > 1 and let a be any real
number. If p(a) = 0 then (x-a) is a factor of p(x).
Proof :-
Let f(a) = 0
On dividing f(x) by 9x-a), let g(x) be the quotient. Also, by remainder
theorem, when f(x) is divided by (x-a), then the remainder is f(a).
Therefore ,f(x) = (x-a)*g(x) + f(a) [Since,f(a) = 0 (given)]
Therefore,(x-a) is a factor of f(x).

9. Algebraic Identities :-
(x+y) 2 = x 2 +2xy+y2
(x-y) 2 = x 2 -2xy+y 2
(x+y) (x-y) = x 2 -y 2
(x+y+z) 2 = x 2 +y 2 +z2 +2xy+2yz+2zx
x 3 +y 3 = (x+y)(x 2 -xy+y 2)
x 3 -y 3 = (x-y)(x 2 +xy+y2)
(x+y) 3 = x 3 +y 3 +3xy(x+y)
(x-y )3 = x3 -y 3 -3xy(x-y)
x 3 +y 3 +z3 -3xyz = (x+y+z)(x 2 +y 2 +z 2 -xy-yz-zx)
If x+y+z =0,then x 3 +y 3 +z3 = 3xyz