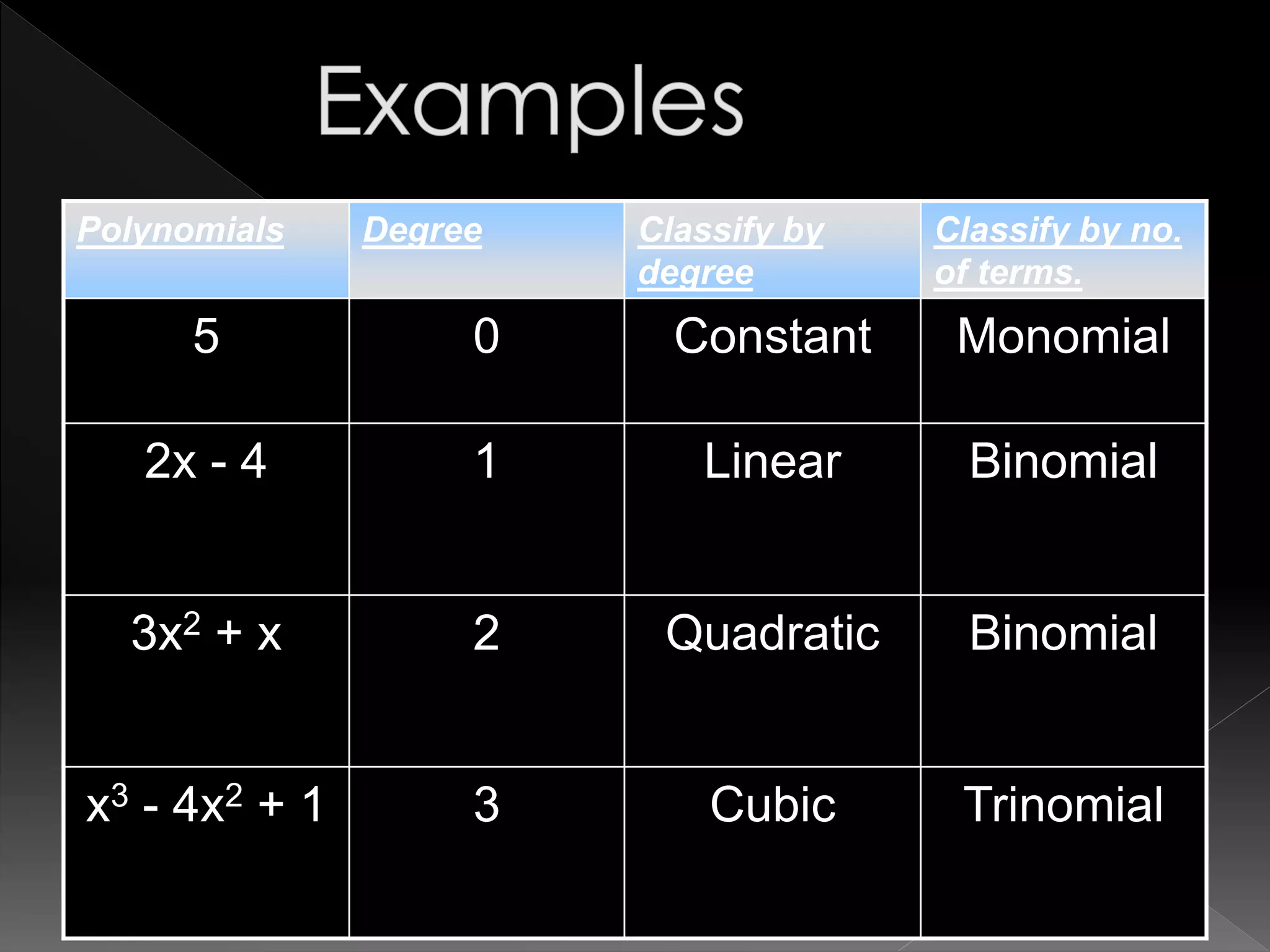
The document defines polynomials and discusses their properties. A polynomial is an algebraic expression involving variables, constants, and exponents that can be combined using addition, subtraction, and multiplication, but not division. Polynomials are classified based on their degree, with monomials having degree 1, binomials degree 2, and trinomials degree 3. The document also discusses factoring polynomials and finding zeros of polynomials.

2. A polynomial is an expression made with
constants, variables and exponents, which are
combined using addition, substraction and
multiplication but not division.
The exponents can only be 0,1,2,3…. etc.
A polynomial cannot have infinite number of
terms.

3.  Monomial
 Binomial
 Trinomial

4. Algebric expression that consists only
one term is called monomial.

5. Algebric expression that consists two
terms is called binomial.

6. Algebric expression that consists three
terms is called trinomial.

7. The exponent of the highest degree term in a
polynomial is known as its degree.

8. Types of polynomial on the basis of degree are :
Linear polynomial: A polynomial of degree 1 is called
a linear polynomial.
Quadratic polynomial: A polynomial of degree 2 is
called a quadratic polynomial.
Cubic polynomial : A polynomial of degree 3 is
called a cubic polynomial.
Biquadratic polynomial : A polynomial of degree 4 is
called a biquadratic polynomial.

9. Polynomials Degree Classify by
degree
Classify by no.
of terms.
5 0 Constant Monomial
2x - 4 1 Linear Binomial
3x2 + x 2 Quadratic Binomial
x3 - 4x2 + 1 3 Cubic Trinomial

11. Let f(x) be a polynomial of degree n > 1 and let a be any real number.
When f(x) is divided by (x-a) , then the remainder is f(a).
PROOF Suppose when f(x) is divided by (x-a), the quotient is g(x) and the remainder
is r(x).
Then, degree r(x) < degree (x-a)
degree r(x) < 1 [ therefore, degree (x-a)=1]
degree r(x) = 0
r(x) is constant, equal to r (say)
Thus, when f(x) is divided by (x-a), then the quotient is g9x) and the remainder is r.
Therefore, f(x) = (x-a)*g(x) + r (i)
Putting x=a in (i), we get r = f(a)
Thus, when f(x) is divided by (x-a), then the remainder is f(a).

12. Let f(x) be a polynomial of degree n > 1 and let a be
any real number.
(i) If f(a) = 0 then (x-a) is a factor of f(x).
PROOF let f(a) = 0
On dividing f(x) by 9x-a), let g(x) be the quotient. Also,
by remainder theorem, when f(x) is divided by (x-a),
then the remainder is f(a).
therefore f(x) = (x-a)*g(x) + f(a)
f(x) = (x-a)*g(x) [therefore f(a)=0(given]
(x-a) is a factor of f(x).

13. Some common identities used to factorize polynomials
(x+a)(x+b)=x2+(a+b)x+a(a+b)2=a2+b2+2ab (a-b)2=a2+b2-2ab a2-b2=(a+b)(a-b)

14. Advanced identities used to factorize polynomials
(x+y+z)2=x2+y2+z2
+2xy+2yz+2zx
(x-y)3=x3-y3-
3xy(x-y)
(x+y)3=x3+y3
+3xy(x+y)
x3+y3=(x+y) *
(x2+y2-xy) x3-y3=(x+y) *
(x2+y2+xy)

15. 1) Polynomials of degree 1, 2 & 3 are called
linear,
quadric and cubic polynomials respectively.
2) A quadric polynomial can have at most two
zeros and
a cubic polynomial can have three zeros.
3) If we are given with the sum and product of
zeros we can find the polynomial by the
following formula:
K[x2+(sum of zeros)x+(Product of zeros)]

16. 4) If two zeros of a polynomial are given then we can
find the third zero by the following steps:
 Convert the zeros into factors of the polynomial
 Make a combined factor by multiplying the
two
factors
 Now divide the polynomial by the combined
factor
 Write the quotient separately
 Do middle term splitting
By this process, we can find the third zero of the
polynomial.

17.  A real number ‘a’ is a zero of a polynomial p(x) if
p(a)=0. In this case, a is also called a root of the
equation p(x)=0.
 Every linear polynomial in one variable has a unique
zero, a non-zero constant polynomial has no zero,
and every real number is a zero of the zero
polynomial.

18. Click here to start
again .