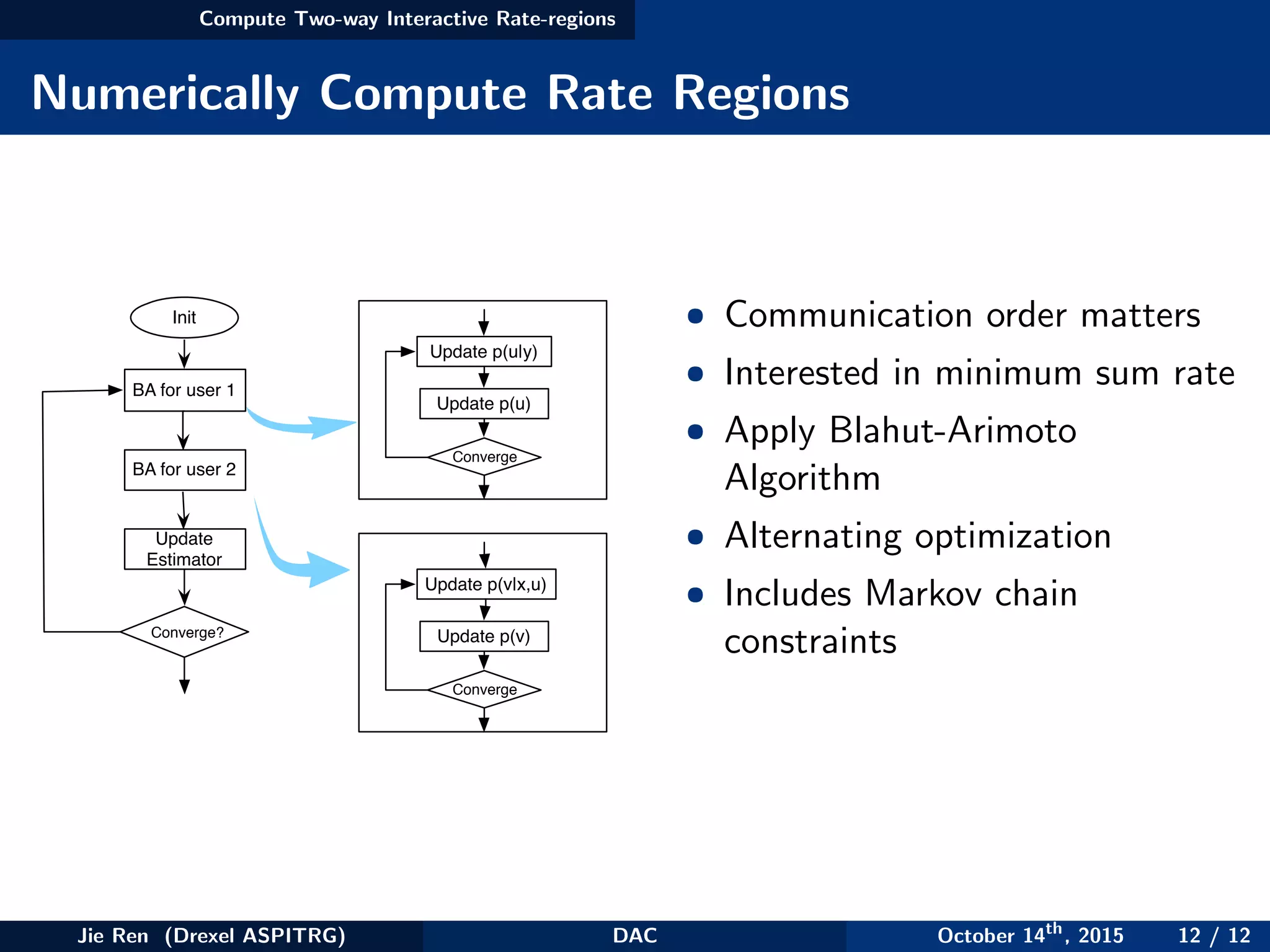
This document discusses distributed arg-max computation. It introduces the problem of computing the maximum value among distributed data sources in a lossless manner using either one-way or interactive communication. For one-way communication, it presents achievability results using graph coloring and a converse based on graph entropy. For interactive communication, it proposes a threshold-based interaction scheme and analyzes the achievable rate using policy iteration. Finally, it discusses numerically computing the two-way interactive rate regions using an adaptation of the Blahut-Arimoto algorithm.

1. Distributed Arg-max Computation
Jie Ren
jr843@drexel.edu
John MacLaren Walsh
jmw96@drexel.edu
Adaptive Signal Processing and Information Theory Group
Department of Electrical and Computer Engineering
Drexel University, Philadelphia, PA 19104
This research has been supported by the Air Force Research Laboratory
under agreement number FA9550-12-1-0086.
October 14th, 2015
Jie Ren (Drexel ASPITRG) DAC October 14th
, 2015 1 / 12

2. Introduction
Outline
1 Introduction
2 Lossless One-way
3 Lossless Interactive
4 Compute Two-way Interactive Rate-regions
Jie Ren (Drexel ASPITRG) DAC October 14th
, 2015 2 / 12

3. Introduction
Motivation – Resource Allocation in LTE
MS 1
MS 2
BS
Encoder
Encoder
Decoder
Subband index
User
subband
gain
1 2 3
Subband index
User
subband
gain
1 2 3
X
(1)
1 , . . . , X
(M)
1
X
(1)
2 , . . . , X
(M)
2
S1
Subband index
User
subband
gain
1 2 3
Z(1)
, . . . , Z(M)
Z(j)
= arg max
n
X
(j)
1 , X
(j)
2
o
Z = g(X1, X2)
ˆZ = f(S1, S2)
S2
Jie Ren (Drexel ASPITRG) DAC October 14th
, 2015 3 / 12

4. Introduction
Problem Model
Z 2 g(XS
1 , . . . , XS
N )
lim
S!1
P(S)
e = 0
R1
R2
RN
Enc1
Dec
XS
2
XS
N
XS
1
Enc2
EncN
• Channel capacity: modeled as
discrete i.i.d. sources
• Assume rateless data
transmission
• The CEO needs to compute
{i|Xi = max{Xi : i ∈ [N]}}
• Distortion Measure
dA((X1,s, . . . , XN,s), ˆZA(s)) =
0 if ˆZA ∈ ZA
ZM(s) − XˆZA(s),s otherwise
(1)
• Distributed Lossless Computation
E d((X1, . . . , XN), ˆZ) = 0 (2)
Jie Ren (Drexel ASPITRG) DAC October 14th
, 2015 4 / 12

5. Lossless One-way
Outline
1 Introduction
2 Lossless One-way
3 Lossless Interactive
4 Compute Two-way Interactive Rate-regions
Jie Ren (Drexel ASPITRG) DAC October 14th
, 2015 5 / 12

6. Lossless One-way
Lossless One-way Results
• Candidate arg-max functions
RA = min
fN ∈FA,N
N
n=1
min
cn∈C(Gn(fN ))
H(cn(Xn)) (3)
• Achievability: build f ∗
N recursively, graph coloring
• Converse: graph entropy
• i.i.d. sources: do not need the OR-product graph
Jie Ren (Drexel ASPITRG) DAC October 14th
, 2015 6 / 12

7. Lossless Interactive
Outline
1 Introduction
2 Lossless One-way
3 Lossless Interactive
4 Compute Two-way Interactive Rate-regions
Jie Ren (Drexel ASPITRG) DAC October 14th
, 2015 7 / 12

8. Lossless Interactive
Problem Model
3 dB
2 dB
2 dB
Ut( t = 3dB)
X1
X2
X3
V 1
t = 1
V 2
t = 0
V 3
t = 0
Notations
• Xi ∈ Xt = {at, . . . , bt}
• Ut Broadcasting message at
round t
• V i
t Replied message from MS i
at round t
Achievable Interaction Scheme
1: CEO broadcasts a threshold λt
at round t
2: User i replies a 1 if Xi ≥ λt and
0 otherwise
3: Stops when CEO knows arg-max
reliably
Jie Ren (Drexel ASPITRG) DAC October 14th
, 2015 8 / 12

9. Lossless Interactive
Analysis
Aggregate rate
Rt(λ) = H(λ|λ1, · · · , λt−1) + Nt + (Ft(λ))Nt
R∗
(Nt, at, λ)
+
Nt
i=1
(1 − Ft(λ))i
Ft(λ)Nt −i Nt!
i!(Nt − i)!
R∗
(i, λ, bt) (4)
Policy Iteration
λ∗
t = arg min
λ
Rt(λ) (5)
Jie Ren (Drexel ASPITRG) DAC October 14th
, 2015 9 / 12

10. Compute Two-way Interactive Rate-regions
Outline
1 Introduction
2 Lossless One-way
3 Lossless Interactive
4 Compute Two-way Interactive Rate-regions
Jie Ren (Drexel ASPITRG) DAC October 14th
, 2015 10 / 12

11. Compute Two-way Interactive Rate-regions
Background
Interactive Communication
User A User B
X Y
U, Ry
V, Rx
f(x, y)
{(rx,ry) :rx ≥ I(V ;X|U,Y ) ry ≥ I(U;Y |X)
where U − Y − X and V − (U,X) − Y
with E[d(f(x,y),φ(v,y))] ≤ D}
• Interaction for Lossy Source
Reproduction (Kaspi 1985)
• Two-way Interaction Function
Computation (Orlitsky & Roche
2001)
• Interaction for function
computation (Ishwar & Ma
2011)
Jie Ren (Drexel ASPITRG) DAC October 14th
, 2015 11 / 12

12. Compute Two-way Interactive Rate-regions
Numerically Compute Rate Regions
BA for user 1
BA for user 2
Update
Estimator
Converge?
Init
Update p(u|y)
Update p(u)
Converge
Update p(v|x,u)
Update p(v)
Converge
• Communication order matters
• Interested in minimum sum rate
• Apply Blahut-Arimoto
Algorithm
• Alternating optimization
• Includes Markov chain
constraints
Jie Ren (Drexel ASPITRG) DAC October 14th
, 2015 12 / 12