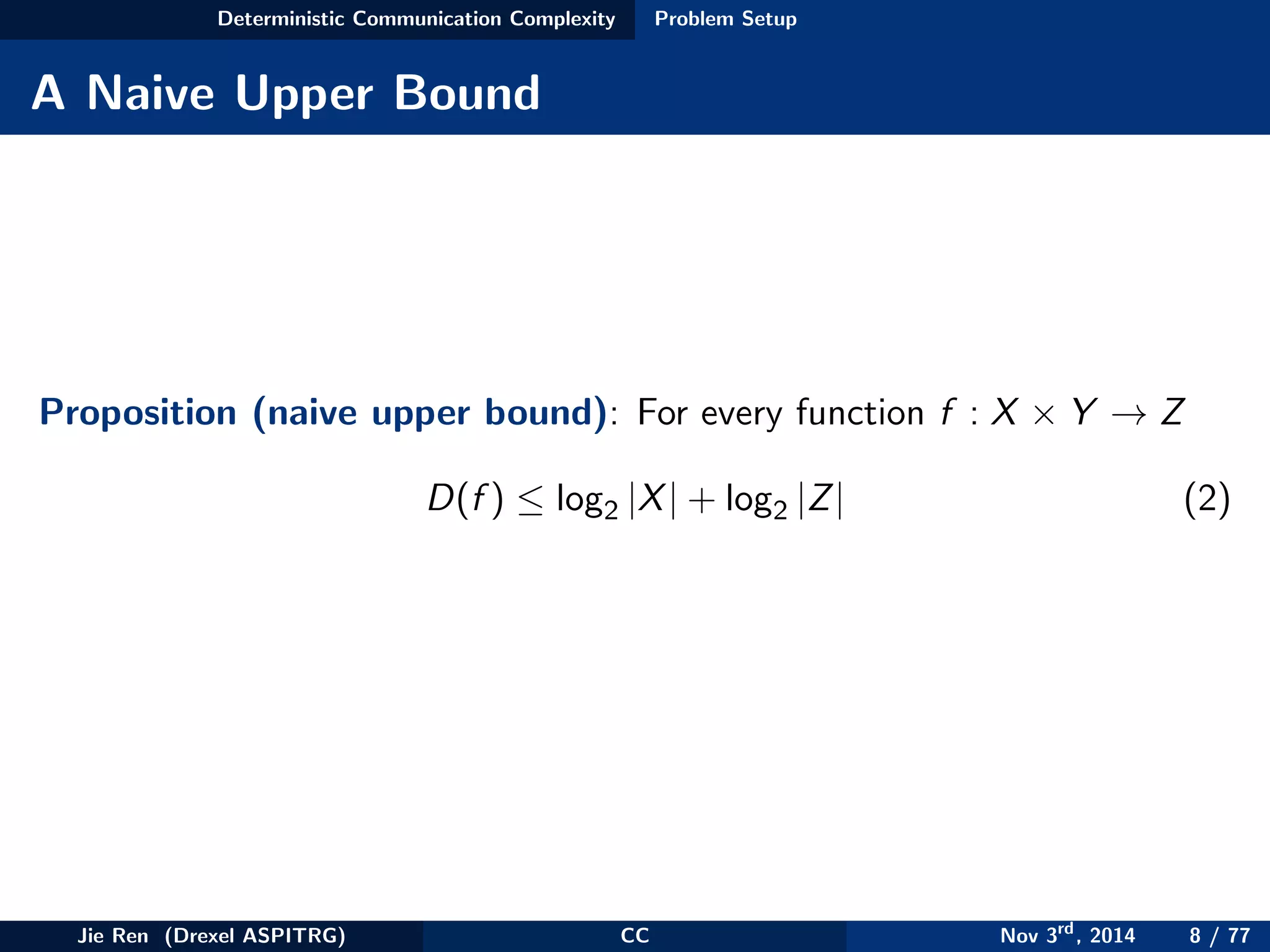
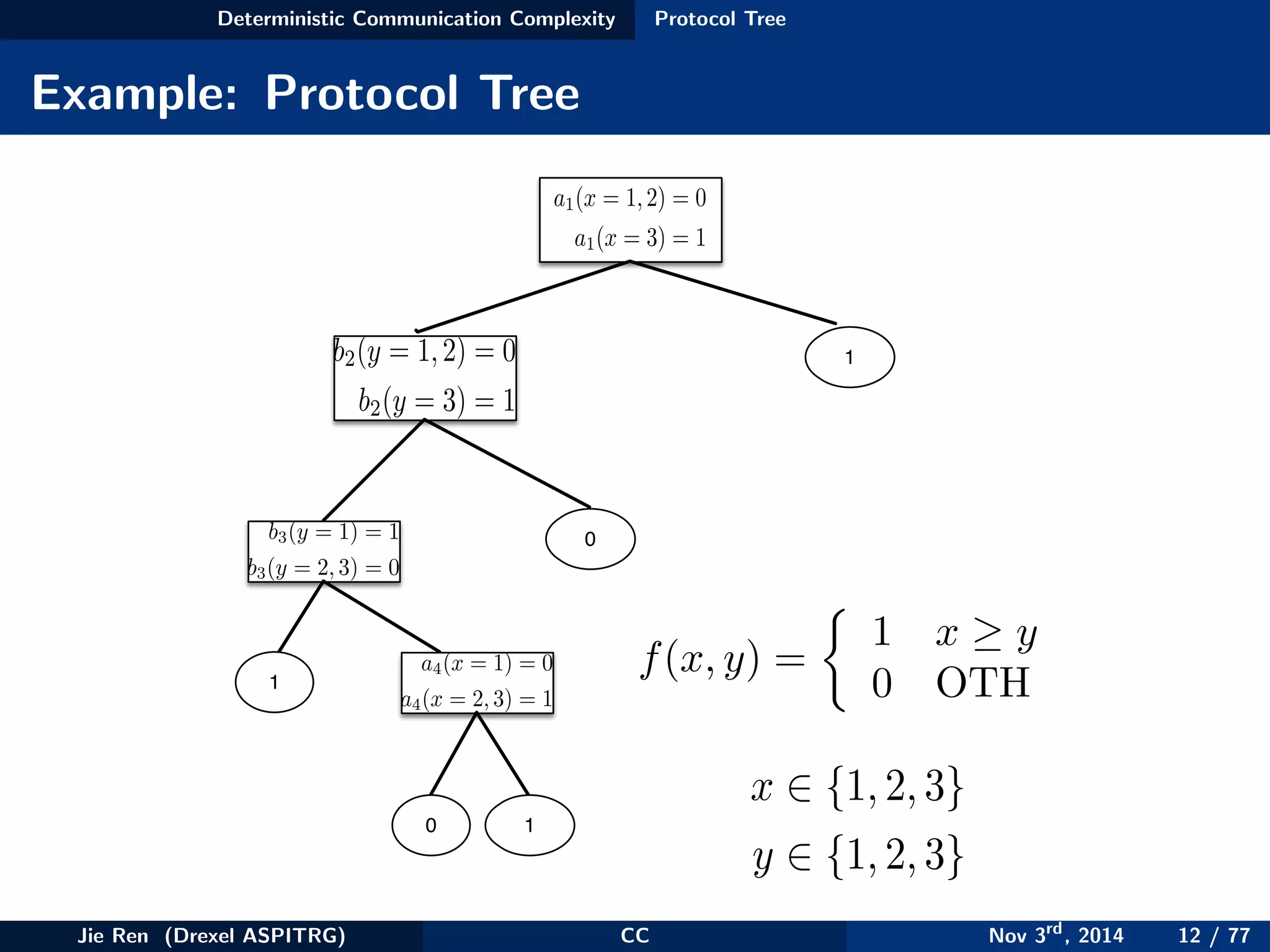
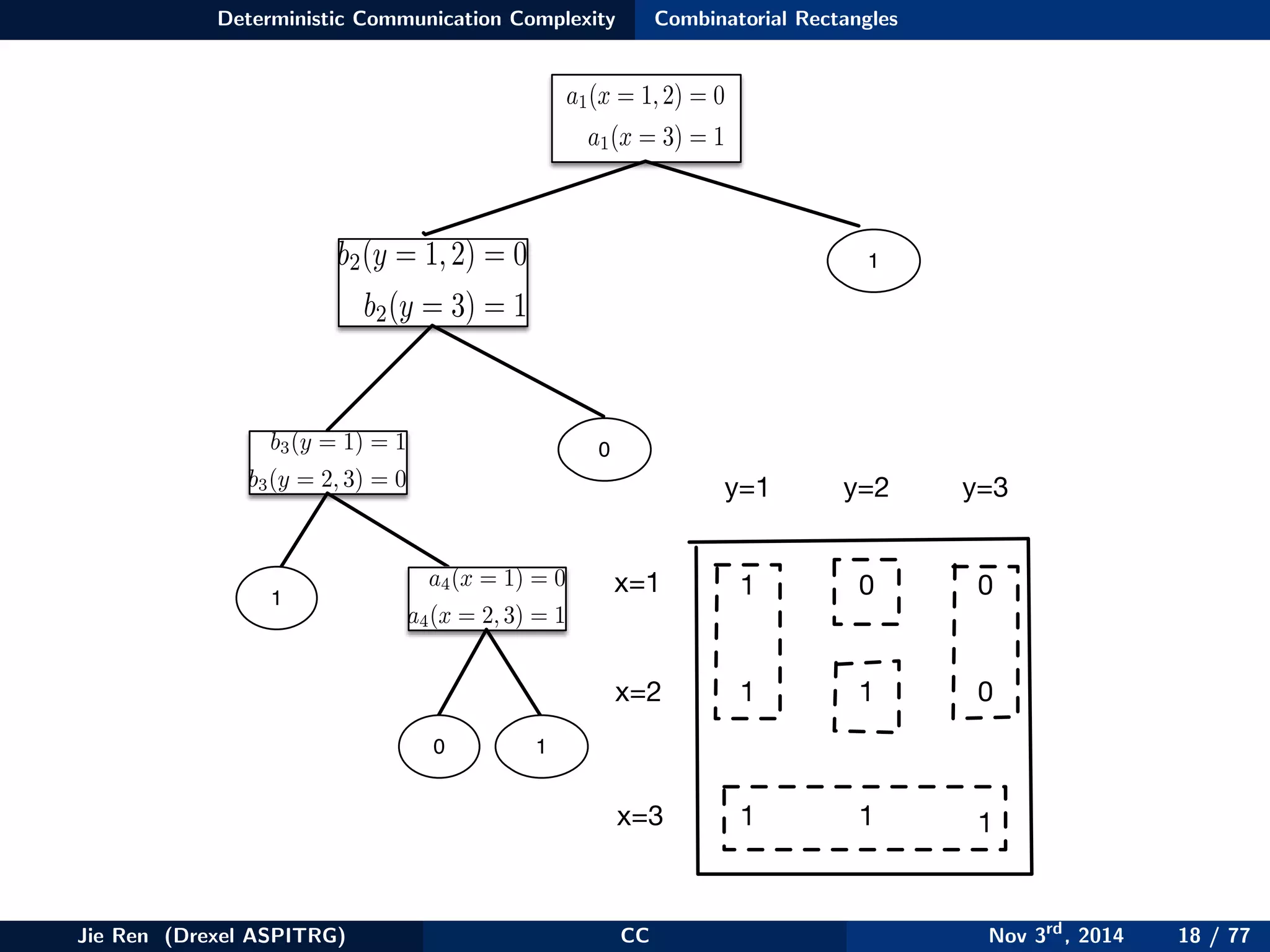
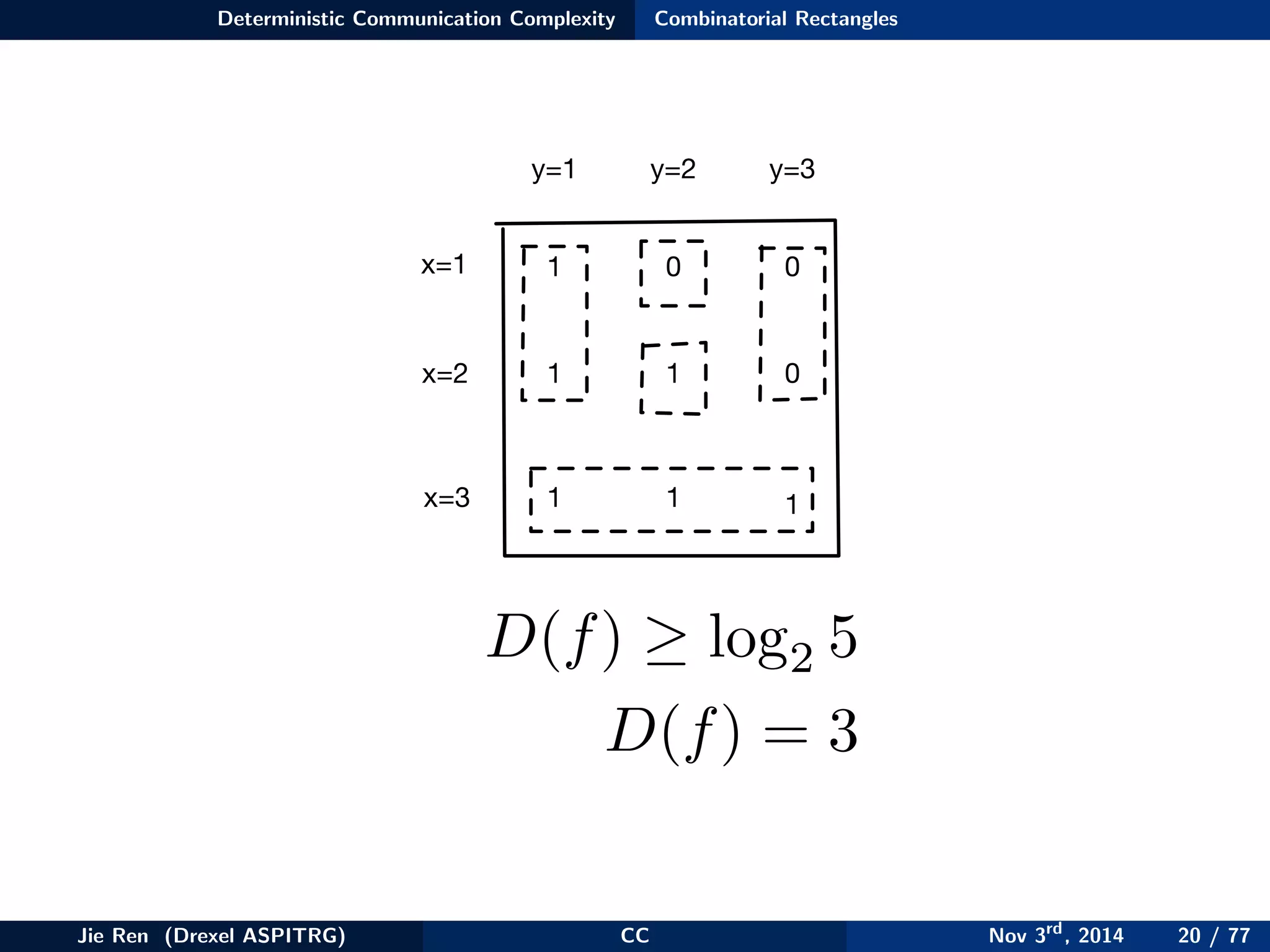
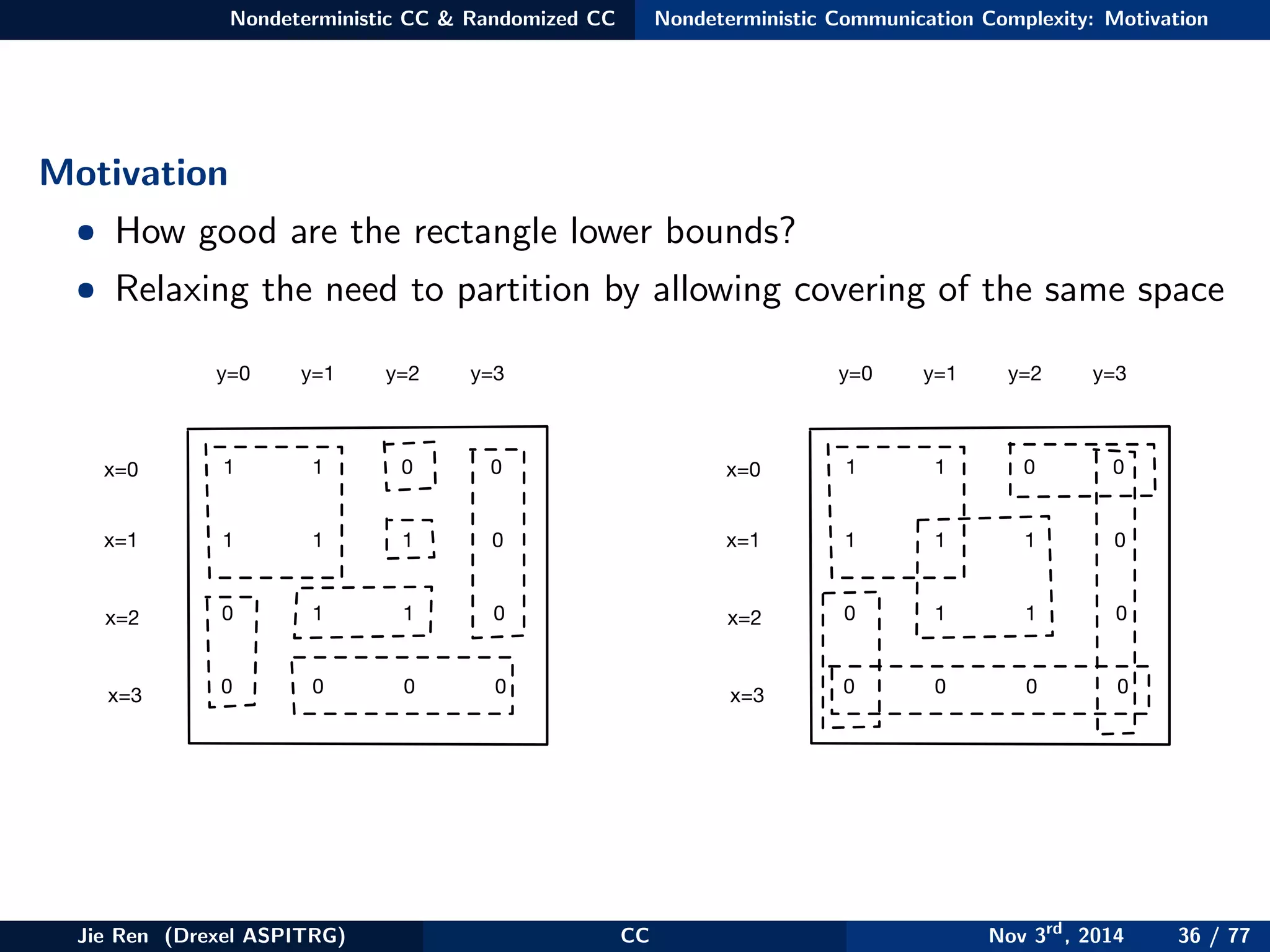
This document provides an overview of communication complexity and deterministic communication complexity. It begins with defining the problem setup, which involves two parties (Alice and Bob) trying to compute a function f based on their private inputs using the minimum communication. It then discusses protocol trees, which model communication protocols, and shows they partition the input space into rectangles. It introduces combinatorial rectangles and shows how the minimum number of rectangles needed to partition the space can provide a lower bound on communication complexity. The document also discusses fooling sets, another technique to lower bound communication complexity, and previews upcoming topics on nondeterministic and randomized communication complexity.












































![Nondeterministic CC & Randomized CC Randomized Communication Complexity
Definition: Let P be a randomized protocol. All the probabilities below
are over random choices of rA and rB.
• P computes a function f with zero error
• P computes a function f with −error if for all (x, y)
P[P(x, y) = f (x, y)] ≥ 1 − (26)
• P computes a function f with one-sided −error if for all (x, y) such
that f (x, y) = 0
P[P(x, y) = 0] = 1, (27)
and for all (x, y) such that f (x, y) = 1,
P[P(x, y) = 1] ≥ 1 − (28)
Jie Ren (Drexel ASPITRG) CC Nov 3rd
, 2014 50 / 77](https://image.slidesharecdn.com/00d94d57-e034-40a9-820b-9e25fe7ae580-150309221050-conversion-gate01/75/CommunicationComplexity1_jieren-50-2048.jpg)


![Nondeterministic CC & Randomized CC Randomized Communication Complexity
Proposition: Given a protocol P that makes an error /2 and the average
number of bits exchanged is t, it can always be modified as follows:
execute P as long as at most 2t/ bits are exchanged, if the protocol
finishes, use its output, otherwise output 0. This gives a worst case cost
2t/ with error upper bounded by .
Proof:
t =
ra,rb,x,y
cc · p(ra, rb, x, y)
=
cc≤2t/
cc · p(ra, rb, x, y) +
cc>2t/
cc · p(ra, rb, x, y)
≥
cc>2t/
cc · p(ra, rb, x, y) ≥
2t
Pr[cc > 2t/ ]
(29)
Hence,
Pr[err] ≤
2
Pr[P ends] + 1 · Pr[P not ends]
≤
2
+
t
2t/
=
(30)
Jie Ren (Drexel ASPITRG) CC Nov 3rd
, 2014 53 / 77](https://image.slidesharecdn.com/00d94d57-e034-40a9-820b-9e25fe7ae580-150309221050-conversion-gate01/75/CommunicationComplexity1_jieren-53-2048.jpg)
![Nondeterministic CC & Randomized CC Randomized Communication Complexity
1 For all 0 < ≤ < 1/2,
R (f ) ≤ O(log · R (f )) (31)
2 For all 0 < ≤ 1/2,
R (f ) ≤ R1
(f ) ≤ O(log −1
R0(f )) (32)
3 For all 0 < ≤ 1/2,
R0(f ) = Θ(max[R1
(f ), R1
(not(f ))]) (33)
Jie Ren (Drexel ASPITRG) CC Nov 3rd
, 2014 54 / 77](https://image.slidesharecdn.com/00d94d57-e034-40a9-820b-9e25fe7ae580-150309221050-conversion-gate01/75/CommunicationComplexity1_jieren-54-2048.jpg)

![Nondeterministic CC & Randomized CC Randomized Communication Complexity
Proof of Property 1: Given a randomized protocol P with worst case
cost T bits and one-sided error no greater than < 1/2, we can build a
new protocol P with worst case cost nT bits by simply running P n
times. In the new protocol, Alice and Bob will claim f (x, y) = 1 if and
only if there exists at least one time among the n repeating protocols that
they will output 1. Now we bound the error for the new protocol P :
P[err|f (x, y) = 0] = 0 (35)
P[err|f (x, y) = 1] = P[all n trails output 0|f (x, y) = 1]
= ( )n
(36)
Therefore, if we repeat P log times, we can guarantee to reduce the
one-sided error to .
Jie Ren (Drexel ASPITRG) CC Nov 3rd
, 2014 56 / 77](https://image.slidesharecdn.com/00d94d57-e034-40a9-820b-9e25fe7ae580-150309221050-conversion-gate01/75/CommunicationComplexity1_jieren-56-2048.jpg)
![Nondeterministic CC & Randomized CC Randomized Communication Complexity
Proof of Property 1: Now we prove property 1. We still run P n times,
each gives an output Xi , i ∈ {1, . . . , n}. In the new protocol, Alice and
Bob will claim f (x, y) = 1 if and only if
1
n
i
Xi >
1
2
(37)
Now we bound the error for the new protocol P :
P[err|f (x, y) = 0] ≤
n
i= n/2
n
i
( )i
(1 − )n−i
≤ ( )n
(38)
P[err|f (x, y) = 1] ≤
n
i= n/2
n
i
( )i
(1 − )n−i
≤ ( )n
(39)
Therefore, if we repeat P log times, we can also guarantee to reduce
the two-sided error to .
Jie Ren (Drexel ASPITRG) CC Nov 3rd
, 2014 57 / 77](https://image.slidesharecdn.com/00d94d57-e034-40a9-820b-9e25fe7ae580-150309221050-conversion-gate01/75/CommunicationComplexity1_jieren-57-2048.jpg)


![Nondeterministic CC & Randomized CC Distributional Complexity and Discrepancy
Discrepancy
Motivation: Allow those rectangles that partition the support to be
“almost” f -monochromatic.
Definition: Let f : X × Y → {0, 1} be a function, R be any rectangle,
and µ be a probability distribution on X × Y , Denote
Discµ(R, f ) = |P
µ
[f (x, y) = 0 & (x, y) ∈ R] − P
µ
[f (x, y) = 1 & (x, y) ∈ R]|
(40)
The discrepancy of f according to µ is,
Discµ(f ) = max
R
Discµ(R, f ) (41)
Jie Ren (Drexel ASPITRG) CC Nov 3rd
, 2014 60 / 77](https://image.slidesharecdn.com/00d94d57-e034-40a9-820b-9e25fe7ae580-150309221050-conversion-gate01/75/CommunicationComplexity1_jieren-60-2048.jpg)

![Nondeterministic CC & Randomized CC Distributional Complexity and Discrepancy
Discrepancy
Proof: Given any P with c bits to compute f , we have
2 ≤ P[P(x, y) = f (x, y)] − P[P(x, y) = f (x, y)]
= (P[P(x, y) = f (x, y)&(x, y) ∈ R ]
−P[P(x, y) = f (x, y)&(x, y) ∈ R ])
≤ |P
µ
[f (x, y) = 0 & (x, y) ∈ R ] − P
µ
[f (x, y) = 1 & (x, y) ∈ R ]|
≤ 2c
· Discµ(f )
(43)
Jie Ren (Drexel ASPITRG) CC Nov 3rd
, 2014 62 / 77](https://image.slidesharecdn.com/00d94d57-e034-40a9-820b-9e25fe7ae580-150309221050-conversion-gate01/75/CommunicationComplexity1_jieren-62-2048.jpg)














