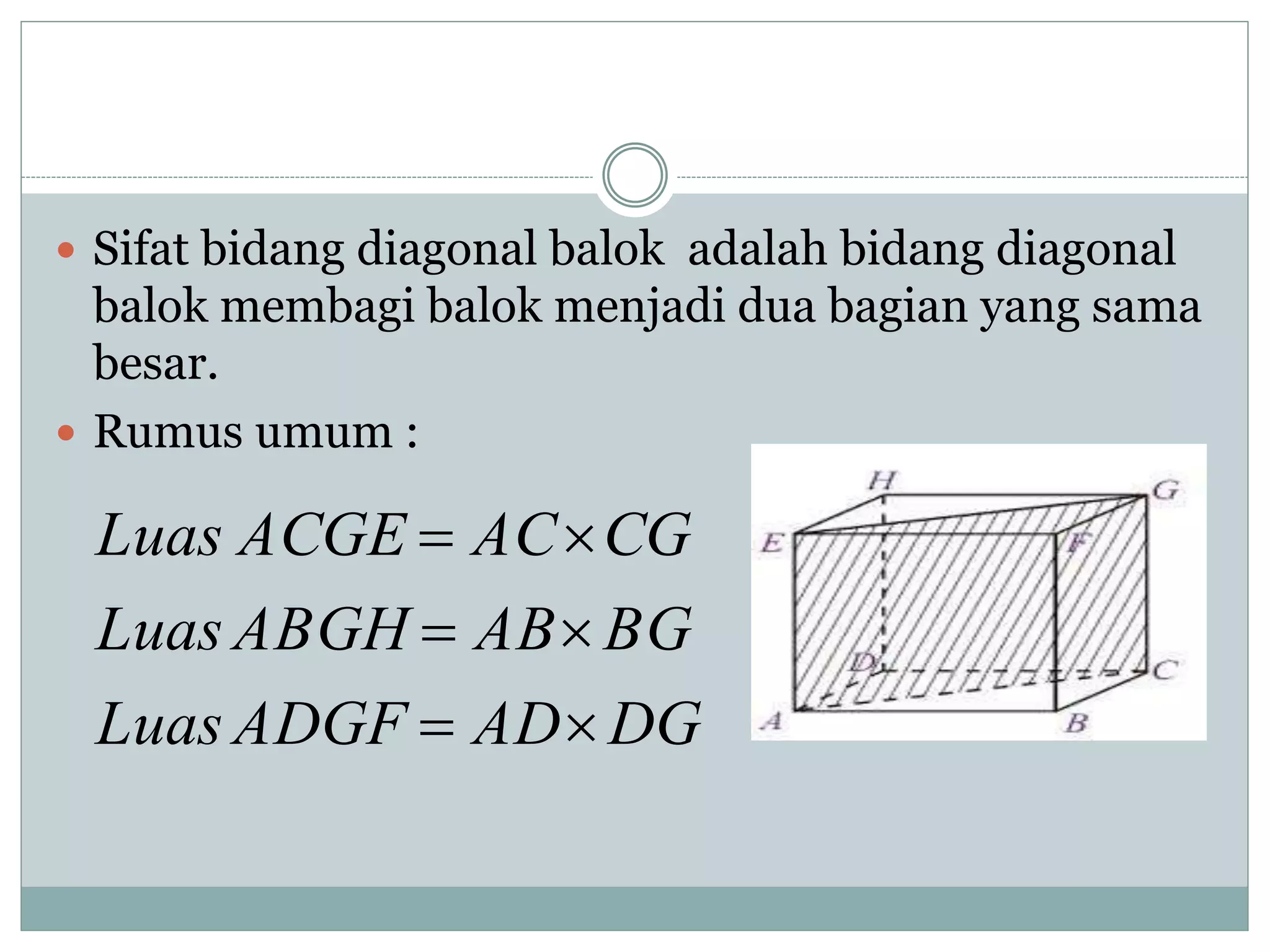
Dokumen ini membahas tentang diagonal balok, termasuk pengertian, jumlah, sifat, dan rumus masing-masing diagonal. Terdapat dua jenis diagonal yaitu diagonal sisi dan diagonal ruang, serta penjelasan mengenai bidang diagonal balok. Selain itu, dokumen ini juga menyajikan rumus panjang rusuk, luas permukaan, dan volume balok.

1. DIAGONAL BALOK
PRESENTASI MATEMATIKA

2. KELOMPOK VI
 Ida Ayu Amanda Dewi Wikannanda 05
 Ni Nyoman Ayu Cyntia Diantari 08
 Prayogi Prasetyoputra Pramono 30
 Putu Sacha Anggita Yundra 33
 Anak Agung Wulanatalia Wiraputri 38

3. Diagonal Balok
 Indikator :
A. Menjelaskan :
1. Pengertian
2. Jumlahnya dan sifatnya
3. Gambarnya
4. Rumus umumnya
Masing-masing terdiri :
1. Diagonal sisi balok
2. Diagonal ruang balok
3. Bidang diagonal balok
B. Menjelaskan rumus :
1. Jumlah panjang rusuk
2. Luas permukaan
3. Volume dari balok

4. Diagonal Sisi Balok
 Diagonal sisi / bidang suatu balok adalah ruas garis
yang menghubungkan dua titik sudut yang
berhadapan pada sebuah sisi.
 Jumlah diagonal sisi/bidang suatu balok adalah dua
belas.
Panjang diagonal sisi AC = BD = EG = HF
Panjang diagonal sisi AF = BE = CH = DG
Panjang diagonal sisi AH = DE = BG = CF

5.  Sifat diagonal sisi balok adalah diagonal sisi
balok saling berpotongan di tengah-tengah dan
membagi dua diagonal sisi sama panjang.
 Rumus umum :
22
22
22
EHAEAH
BFABAF
BCABAC




6. Diagonal Ruang Balok
 Diagonal ruang sebuah balok adalah ruas garis
yang menghubungkan dua titik sudut
berhadapan dalam balok.
 Jumlah diagonal ruang balok adalah 4 buah.
 Panjang diagonal ruang AG = BH = CE = AF

7.  Sifat-sifat diagonal ruang balok adalah diagonal
ruang balok saling berpotongan di tengah-tengah
dan membagi dua diagonal ruang sama panjang.
 Rumus umum :
22
ACEACE 

8. Bidang Diagonal Balok
 Bidang diagonal balok adalah bidang yang melalui
dua buah rusuk yang berhadapan.
 Balok memiliki 6 buah bidang diagonal, yaitu :
ACGE, BDHF, ABGH, CDEF, ADGF, BCHE
 Bidang diagonal ACGE = BDHF, ABGH = CDEF,
ADGF, BCHE.

10.  Sifat bidang diagonal balok adalah bidang diagonal
balok membagi balok menjadi dua bagian yang sama
besar.
 Rumus umum :
DGADADGFLuas
BGABABGHLuas
CGACACGELuas




11. B. Rumus
A. Rumus panjang rusuk balok :
B. Rumus luas permukaan balok :
C. Rumus volume balok :
 tlpRusukPanjang  4
tlpVolume 
      tltplppermukaanLuas  2

12. Presentasi
Matematika
Kelompok VI