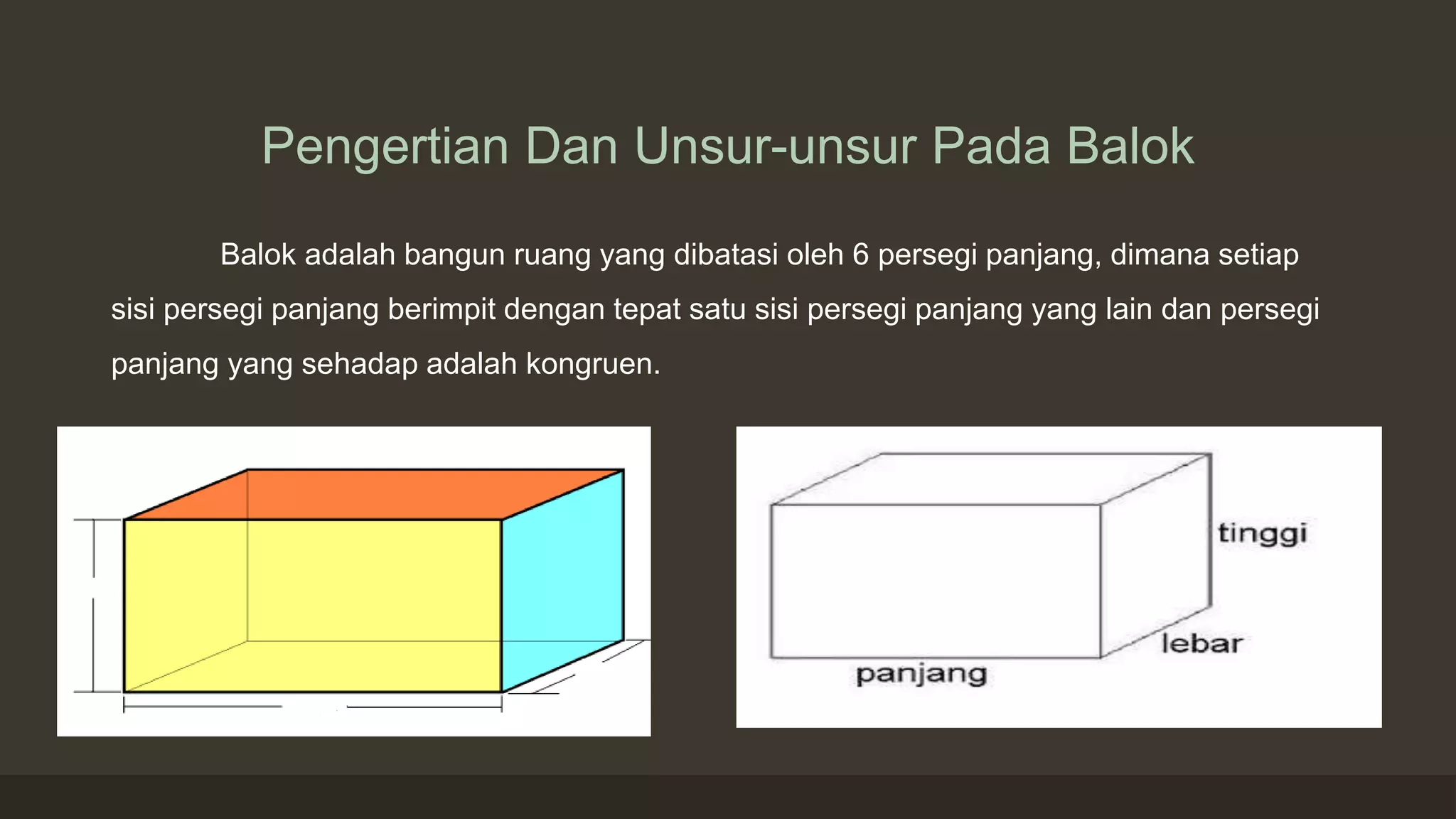
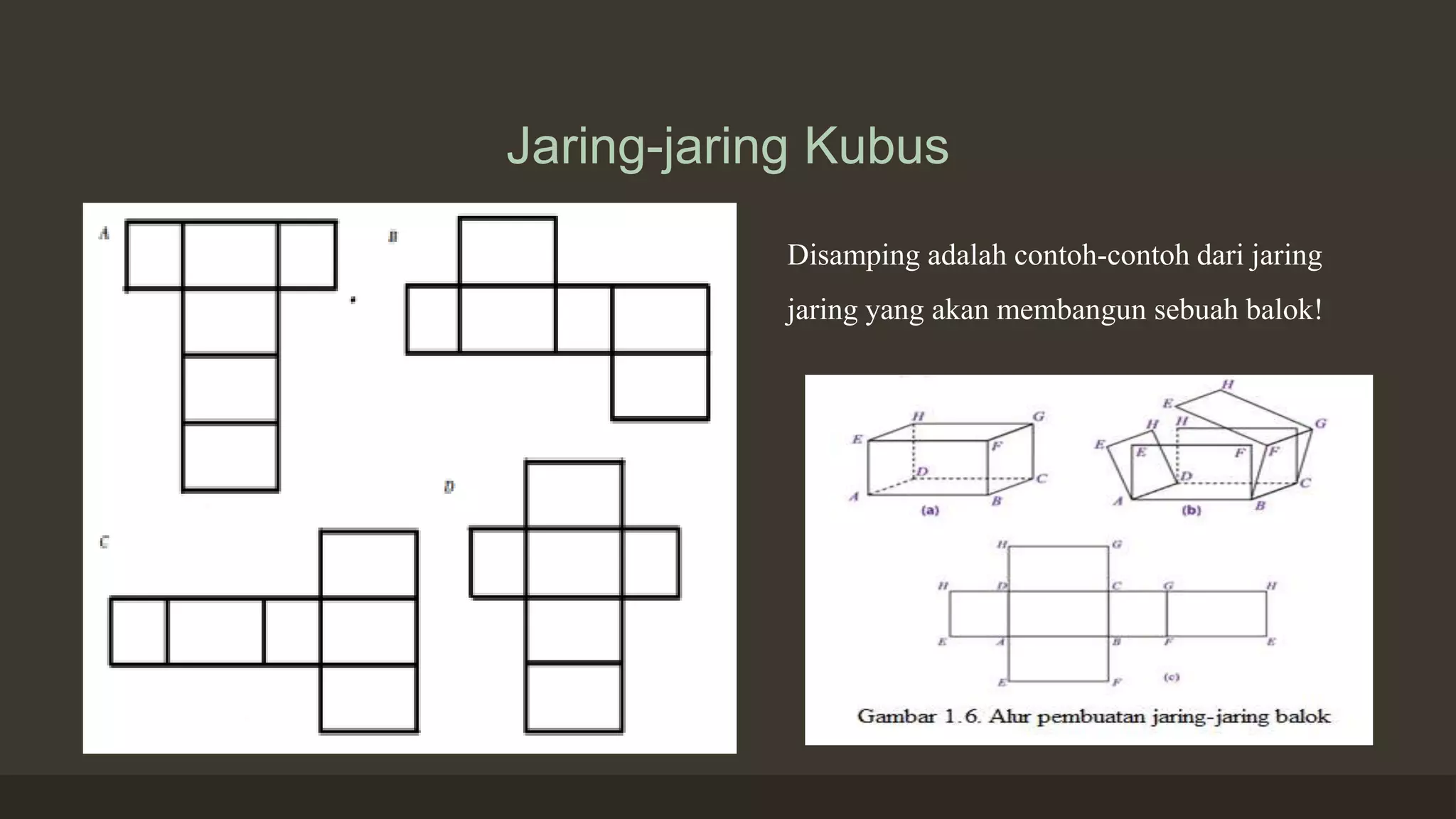
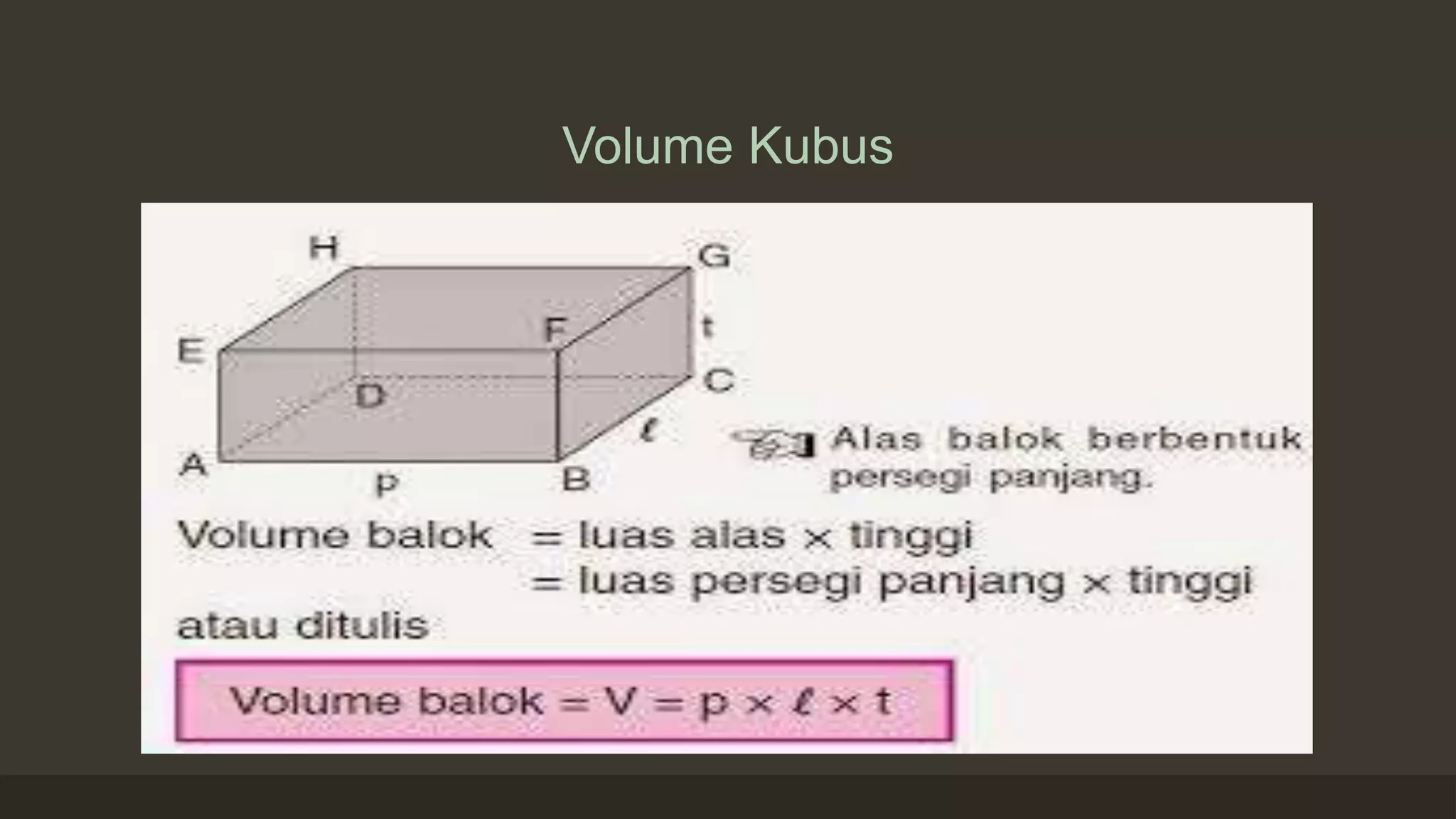
Balok adalah bangun ruang dengan 6 sisi persegi panjang, 12 rusuk, dan 8 sudut yang sama besar. Diagonal pada balok terdiri dari diagonal bidang dan diagonal ruang yang dapat dihitung menggunakan teorema Pythagoras. Luas permukaan balok dapat dihitung dengan rumus 2(pl + pt + lt) dan volumenya mengikuti prinsip yang sama seperti kubus.

1. BALOK

2. Pengertian Dan Unsur-unsur Pada Balok
Balok adalah bangun ruang yang dibatasi oleh 6 persegi panjang, dimana setiap
sisi persegi panjang berimpit dengan tepat satu sisi persegi panjang yang lain dan persegi
panjang yang sehadap adalah kongruen.

3. Bangun ruang balok memiliki sifat-sifat sebagai berikut :
• Memiliki 6 sisi yang ukuran dan modelnya sama (ABCD,
ADEH, ABEF. EFGH, CDGH dan BCFG)
• Memiliki 12 rusuk yang ukurannya sama, 4 rusuk tegak dan
8 rusuk miring (AB, CD, EF, GH, AE, DH, BF, CG, AD, EH,
BC dan FG)
• Memiliki 8 buah sudut yang sama besar yaitu (A, B, C, D,
E, F, G dan H)
• Memiliki ukuran P x L x T
• Memiliki 12 diagonal sisi tetapi tidak semuanya sama
panjang, hanya yang berhadapan saja yang sama panjang
(AF, BE, DG, CH, AH, DE, BG, CF, AC, BD, EG dan FH)
serta 4 diagonal ruang (AG, BH, CE dan DF)

4. Diagonal Bidang Dan Diagonal Ruang Pada Balok
Diagonal bidang adalah garis yang menghubungkan dua titik sudut pada satu
bidang yang ada pada balok. Untuk mencari diagonal bidang pada balok kita menggunakan
teorema Pythagoras yaitu ” BE² = AB² + AE² ” pada satu bidang yang terdapat pada balok

5. Diagonal ruang pada balok yaitu garis Yang menghubungkan dua titik (PV) dan
(TR) yang terletak dalam ruang tersebut ( balok ).

6. Diagonal ruang juga menggunakan teorema Pythagoras untuk menyelesaikannya namun,
perbedaan dalam mengerjakan adalah letak titik-titik yang menjadi garis yang akan
mendiagonalkannya.
Untuk rumus dari diagonal ruang adalah :
HB² = p² + l² + t²

7. Bidang Diagonal
Pada gambar (1) dapat ditunjukan bahwasanya
ABCD.EFGH dapat disekat oleh BDFH yang disebut
bidang diagonal.
Bidang diagonal BDFH dibentuk oleh dua
rusuk yang berhadapan dan sama panjang dan
sejajar, yaitu rusuk BF dan DH. Bidang diagonal BDHF
berbentuk persegi panjang, karena BD // FH, BF // DH
dan BD BF. Dalam kubus semua rusuk mempunyai
panjang yang sejajar dan kongruen, sehingga
perbedaan dalam kubus dan balok hanya ada pada
lebar dan tinggi. Akan tetapi seluruh cara untuk
menentukan diagonal pada kubus sama seperti
menentukan diagonal pada balok.

8. Jaring-jaring Kubus
Disamping adalah contoh-contoh dari jaring
jaring yang akan membangun sebuah balok!

9. Luas Permukaan Kubus
Luas permukaan balok adalah jumlah seluruh luas
bidang yang ada di balok
Jadi dapat disimpulkan bahwa rumus luas
permukaan balok adalah :
Luas permukaan balok = 2 (pl + pt + lt)

10. Volume Kubus

11. SELESAI