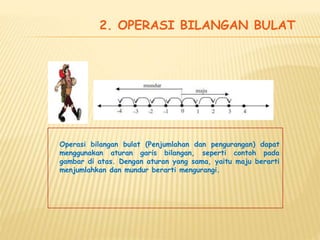
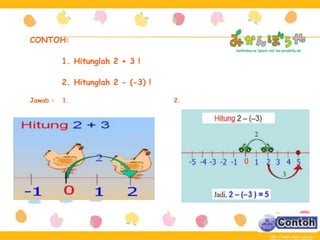
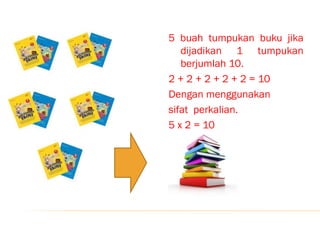
Dokumen ini menjelaskan tentang bilangan bulat, termasuk konsep, operasi, dan sifat-sifatnya. Contoh yang diberikan mencakup penjumlahan, pengurangan, perkalian, dan pembagian bilangan bulat dengan penggunaan garis bilangan. Terdapat juga contoh masalah untuk latihan yang berkaitan dengan aplikasi nyata dari bilangan bulat.

1. BILANGAN BULAT

2. 1. MENEMUKAN KONSEP BILANGAN BULAT
2. OPERASI BILANGAN BULAT

3. Sekarang mari kita cermati data di bawah ini :
● suhu kota Beijing adalah 0 ºc
● suhu kota Jakarta adalah 29 ºc
● suhu kota Alaska adalah -25 ºc
Dari contoh di atas, kita dapat menggambarkan
bilangan-bilangan tersebut (0, 29, -29) ke dalam
garis bilangan.
1. KONSEP BILANGAN BULAT

4. Pada gambar garis bilangan dapat dilihat terdapat
himpunan bilangan yang memiliki sifat dan konsep
yang berbeda, yakni:
1. Hmpunan bilangan Asli dituliskan: A =
{1,2,3,4,...}
2. Himpnan bilangan Cacah dituliskan: C =
{0,1,2,3,4,...}
Himpunan bilangan cacah adalah gabungan
Himpunan Bilangan Asli dan himpunan yang
anggotanya bilangan nol. Itu sama halnya
dengan gabungan himpunan bilangan bulat
positif dan himpunan yang Kumpulan bilangan
cacah adalah gabungan himpunan bilangan asli
dan himpunan yang anggotanya bilangan nol.
3. Himpunan Bilangan Bulat dituliskan Z = {…¸-4,-
3,-2,-1,0,1,2,3,4,…}
Dengan kata lain Himpunan Bilangan Bulat
adalah gabungan himpunan bilangan bulat positif
dan Himpunan Bilangan Bulat Negatif serta
himpunan yang anggotanya bilangan nol.
Himpunan Bilangan
Bulat adalah gabungan
himpunan bilangan bulat
positif dan Himpunan
Bilangan Bulat Negatif
serta himpunan yang
anggotanya bilangan nol.
Important!! ^_^

5. Dari garis bilangan di atas, menjelaskan bahwa garis
bilangan bulat memiliki rambu-rambu aturan, yaitu
apabila ke arah kanan dari 0 merupakan bilangan
bulat positif (nilainya makin besar) dan sebaliknya
apabila ke arah kiri dari 0 merupakan bilangan bulat
negatif (nilainya makin kecil)

6. 2. OPERASI BILANGAN BULAT
Operasi bilangan bulat (Penjumlahan dan pengurangan) dapat
menggunakan aturan garis bilangan, seperti contoh pada
gambar di atas. Dengan aturan yang sama, yaitu maju berarti
menjumlahkan dan mundur berarti mengurangi.

7. CONTOH:
1. Hitunglah 2 + 3 !
2. Hitunglah 2 - (-3) !
Jawab : 1. 2.

8. 3. Perkalian Bilangan Bulat

9. SIFAT PERKALIAN
Dari gambar disamping,
dapat disimpulkan
bahwa bilangan jika
dikali dengan
sejenisnya, maka
hasilnya positif.
Sebaliknya, jika tidak
sejenis ( + dan - ) maka
hasilnya negatif.

10. 1. SIFAT TERTUTUP
3. SIFAT ASOSIATIF
Untuk setiap bilangan bulat
p dan q, selalu berlaku p x q
= r, dengan r juga bilangan
bulat.
2. Sifat komutatif
Untuk setiap bilangan bulat
p dan q, selalu berlaku :
p x q = q x p
Untuk setiap bilangan bulat
p, q, dan r selalu berlaku :
(p x q) x r = p x (q x r)
4. Sifat distributif perkalian
terhadap penjumlahan
Untuk setiap bilangan bulat,
p, q, r
Selalu berlaku :
p x (q + r) = (p x q) + (p x r)

11. 5. Sifat distributif perkalian terhadap pengurangan
Untuk setiap bilangan bulat, p, q, r
Selalu berlaku :
p x ( q - r) = (p x q) – (p x r)
6. Memiliki elemen identitas
Untuk setiap bilangan bulat p, selalu berlaku :
p x 1 = 1 x p = p
elemen identitas pada perkalian adalah 1.

12. CONTOH SOAL :
ADA 5 TUMPUKAN BUKU YANG BERISI
MASING-MASING 2 BUKU, BERAPA
JUMLAH SEMUANYA JIKA
DIKUMPULKAN MENJADI SATU
TUMPUKAN?

13. 5 buah tumpukan buku jika
dijadikan 1 tumpukan
berjumlah 10.
2 + 2 + 2 + 2 + 2 = 10
Dengan menggunakan
sifat perkalian.
5 x 2 = 10

14. 3. PEMBAGIAN BILANGAN BULAT
Dari gambar disamping,
dapat disimpulkan bahwa bilangan
jika dibagi dengan sejenisnya,
maka hasilnya positif. Sebaliknya,
jika tidak sejenis ( + dan - ) maka
hasilnya negatif.

15. CONTOH
Disediakan 10 buku ,
tempatkanlah 10 buku
tersebut di 5 tempat
yang berbeda dengan
jumlah yang sama ?

16. 10 buku

17.  Penjelasan :
disediakan 10 buku, dan akan ditempatkan pada
5 tempat yang berbeda dengan jumlah yang
sama .
maka : 10 buku = 2 buku/ tempat
5 tempat

18. Soal-soal Latihan:
1. Harga satu 1 kg alpukat satu bulan yang
lalu Rp6000. Karena musim alpukat,
harganya turun dipasaran hingga Rp 2000
per kg. Cobatentukan harga penurunan
apokat dengan penjumlahan bilangan bulat!
2. Sebuah pesawat Garuda, mula-mula terbang
pada ketinggian 3.000 kaki di atas
permukaan laut, karena gumpalan awan
dekat maka pesawat terbang naik sampai
ketinggian 7.000 kaki. Coba tentukan
kenaikan posisi pesawat dengan penjumlahan
bilangan bulat!

19. 3. Pada kedalaman 180 m, kapal selam harus naik ke permukaan 90 m, karena
ditemukan batu karang yang besar. Di mana posisi kapal selam setelah naik?
Coba anda selesaikan sendiri. Lihat garis bilangan di sebelah kanan untuk
membantu anda!
4. Sebuah kapal selam, mula-mula menyelam 120 m di bawah permukaan laut,
kemudian kapal bergerak ke bawah sejauh 60 m. Coba nyatakan posisi kapal
selam dari permukaan laut dengan penjumlahan bilangan bulat!

20. 5. DIKETAHUI ADA SEBUAH
KOTAK YANG BERISI 7 BUAH
BINTANG.
JIKA ADA 3 KOTAK YANG BERISI
SAMA, BERAPAKAH JUMLAH
SEMUA BINTANG.
6. JIKA ADA SEBUAH PIRING YANG BERISI
APEL SEBANYAK 4 BUAH DAN ADA JUGA
YANG BERISI 5 BUAH APEL. BERAPA JUMLAH
SELURUH APEL JIKA ADA 4 PIRING DENGAN
ISI 4 BUAH SERTA 2 PIRING DENGAN ISI 5
BUAH ?

21. 7. Untuk keperluan ongkos dan uang jajan Alfon ke
sekolah, orangtuanya memberikan uang sebanyak
Rp 50.000,-. Jika setiap hari ongkos dan uang
jajannya adalah Rp 10.000,-, berapa harikah
uang itu akan habis?
8. Hadi memiliki 36 ekor kelinci. Ia
menempatkannya
pada 6 kandang dan banyaknya kelinci
pada setiap
kandang adalah sama.
a. Berapa ekor kelinci ada pada setiap
kandang?
b. Dari tiap kandang diambil 2 ekor
kelinci untuk
dijual kepada Hadi. Berapa ekor kelinci
yang tersisa
seluruhnya?
c. Berapa ekor kelinci yang dijual
kepada Hadi?

22. TERIMA KASIH
SELAMAT
BELAJAR