Predictive Modeling Workshop

PREDICTIVE
MODELING
WORKSHOP
Max Kuhn
O P E N
D A T A
S C I E N C E
C O N F E R E N C E_
BOSTON 2015
@opendatasci

Predictive Modeling Workshop
Max Kuhn, Ph.D
Pfizer Global R&D
Groton, CT
max.kuhn@pfizer.com

Outline
Modeling conventions
Modeling capabilities
Data splitting
Pre–processing
Measuring performance
Over–fitting and resampling
Classificationtrees, boosting
Support vector machines
Extra topics as time allows
Max Kuhn (Pfizer) Predictive Modeling 2 /142

Terminology
Data:
numeric data: numbers of any type (eg. counts, sales price)
categorical or nominal data: non–numeric data (eg. color, gender)
Variables:
outcomes: the data to be predicted
predictors (aka independent variables, descriptors, inputs): data used
to predict the outcome
Models:
classification: models to predict categorical outcomes
regression: models to predict numeric outcomes
(these last two are imperfect definitions)

The Formula Interface
There are two main conventions for specifyingmodels in R: the formula
interface and the non–formula (or “matrix”) interface.
For the former, the predictors are explicitly listed in an R formula that
looks like: outcome ∼ var1 + var2 + ....
For example, the formula
modelFunction(price ~ numBedrooms + numBaths + acres,
data = housingData)
would predict the closing price of a house using three quantitative
characteristics.

The Formula Interface
The shortcut y ∼ . can be used to indicate that all of the columns in the
data set (except y) should be used as a predictor.
The formula interface has many conveniences. For example,
transformations, such as log(acres) can be specified in–line.
Unfortunately, R does not efficiently store the information about the
formula. Using this interface with data sets that contain a large number of
predictors may unnecessarily slow the computations.

The Matrix or Non–Formula Interface
The non–formula interface specifiesthe predictors for the model using a
matrix or data frame (all the predictors in the object are used in the
model).
The outcome data are usually passed into the model as a vector object.
For example:
modelFunction(x = housePredictors, y = price)
In this case, transformations of data or dummy variables must be created
prior to being passed to the function.
Note that not all R functions have both interfaces.

Building and Predicting Models
Almost all modeling functions in R follow the same
workflow:Create the model using the basic function:
fit <- knn(trainingData, outcome, k = 5)
Assess the properties of the model using print, plot. summary or
other methods
Predict outcomes for samples using the predict method:
predict(fit, newSamples).
1
2
3
The model can be used for prediction without changing the original model
object.

Predictive Modeling Methods in R
As previouslymentioned, there is a machine learning Task View page on
the R website that does a good job of describing the range of models
available
parametric regression models: ordinary/generalized/robust
regression models; neural networks; partial least squares; projection
pursuit regression; multivariate adaptive regression splines; principal
component regression
sparse/penalized models: ridge regression; the lasso; the elastic net;
generalized linear models; partial least squares; nearest shrunken
centroids; logistic regression
kernel methods: support vector machines; relevance vector
machines; least squares support vector machine; Gaussian processes
(more)

Predictive Modeling Methods in R
trees/rule–based models: CART; C4.5; conditional inference trees;
node harvest, Cubist, C5.0
ensembles: random forest; boosting (trees, linear models, generalized
additive models, generalized linear models, others); bagging (trees,
multivariate adaptive regression splines), rotation forests
prototype methods: k nearest neighbors; learned vector quantization
discriminant analysis: linear; quadratic; penalized; stabilized; sparse;
mixture; regularized; stepwise; flexible
others: naive Bayes; Bayesian multinomial probit models

Model Function Consistency
Since there are many modeling packages written by different people, there
are some inconsistencies in how models are specified and predictions are
made.
For example, many models have only one method of specifyingthe model
(e.g. formula method only)

Generating Class Probabilities Using Different Packages
obj Class Package predict Function Syntax
lda
glm
gbm
mda
rpart
Weka
LogitBoost
MASS
stats
gbm
mda
rpart
RWeka
caTools
predict(obj) (no options needed)
predict(obj,
predict(obj,
predict(obj,
predict(obj,
predict(obj,
predict(obj,
type
type
type
type
type
type
=
=
=
=
=
=
"response")
"response", n.trees)
"posterior")
"prob")
"probability")
"raw", nIter)

The caret Package
The caret package was developed to:
create a unified interface for modeling and prediction (interfaces to
183 models – up from 112 a year ago)
streamline model tuning using resampling
provide a variety of“helper” functions and classes for day–to–day
model building tasks
increase computational efficiency using parallel processing
First commits within Pfizer: 6/2005, First version on CRAN: 10/2007
Website: http://topepo.github.io/caret/
JSS Paper: http://www.jstatsoft.org/v28/i05/paper
Model List: http://topepo.github.io/caret/bytag.html
Many computing sections in APM

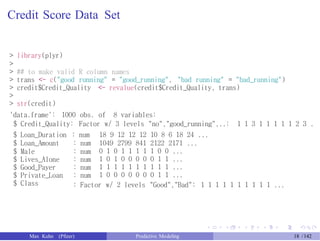
Credit Score Data Set
These data can be found in Multivariate Statistical Modelling Based on
Generalized Linear Models by Fahrmeir et al and are in the Fahrmeir
package.
Data were collected by South German bank to predict whether loan
recipents would be good payers.
The data are moderate size: 1000 samples and 7 predictors.
The outcome was related to whether or not a recipent repayed their loan.
There is a small class imbalance: 70% repayed.
Predictors are related to demographics, credit information and data related
to the loan and bank account.

>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
>
## translations, formatting, and dummy variables
library(Fahrmeir)
data(credit)
credit$Male <-ifelse(credit$Sexo == "hombre", 1, 0)
credit$Lives_Alone <-ifelse(credit$Estc == "vive solo", 1, 0)
credit$Good_Payer <-ifelse(credit$Ppag == "pre buen pagador", 1, 0)
credit$Private_Loan <-ifelse(credit$Uso == "privado", 1, 0)
credit$Class <-ifelse(credit$Y == "buen", "Good", "Bad")
credit$Class <- factor(credit$Class, levels = c("Good", "Bad"))
credit$Y <- NULL
credit$Sexo <- NULL
credit$Uso <- NULL
credit$Ppag <- NULL
credit$Estc <- NULL
names(credit)[names(credit) == "Mes"] <- "Loan_Duration"
names(credit)[names(credit) == "DM"] <- "Loan_Amount"
names(credit)[names(credit) == "Cuenta"] <- "Credit_Quality"

> library(plyr)
>
> ## to make valid R column names
> trans <- c("good running" = "good_running", "bad running" = "bad_running")
> credit$Credit_Quality <- revalue(credit$Credit_Quality, trans)
>
> str(credit)
'data.frame': 1000 obs. of 8 variables:
$ Credit_Quality: Factor w/ 3 levels "no","good_running",..: 1 1 3 1 1 1 1 1 2 3 .
$ Loan_Duration : num 18 9 12 12 12 10 8 6 18 24 ...
1049 2799 841 2122 2171 ...
0 1 0 1 1 1 1 1 0 0 ...
1 0 1 0 0 0 0 0 1 1 ...
1 1 1 1 1 1 1 1 1 1 ...
1 0 0 0 0 0 0 0 1 1 ...
$ Loan_Amount
$ Male
$ Lives_Alone
$ Good_Payer
$ Private_Loan
$ Class
: num
: num
: num
: num
: num
: Factor w/ 2 levels "Good","Bad": 1 1 1 1 1 1 1 1 1 1 ...

General
Strategies
APM Ch 1, 2 and 4.

Model Building Steps
Common steps during model building are:
estimating model parameters (i.e. training models)
determining the values of tuning parameters that cannot be directly
calculated from the data
calculating the performance of the final model that willgeneralize to
new data
How do we“spend” the data to find an optimal model? We typically split
data into training and test data sets:
Training Set: these data are used to estimate model parameters and
to pick the values of the complexity parameter(s) for the model.
Test Set (aka validation set): these data can be used to get an
independent assessment of model efficacy. They should not be used
during model training.

Spending Our Data
The more data we spend, the better estimates we’ll get (provided the data
is accurate). Given a fixed amount of data,
too much spent in training won’t allow us to get a good assessment
of predictive performance. We may find a model that fits the training
data very well, but is not generalizable (over–fitting)
too much spent in testing won’t allow us to get a good assessment of
model parameters
Statistically, the best course of action would be to use all the data for
model building and use statistical methods to get good estimates of error.
From a non–statistical perspective, many consumers of of these models
emphasize the need for an untouched set of samples the evaluate
performance.

Spending Our Data
There are a few different ways to do the split: simple random sampling,
stratified sampling based on the outcome, by date and methods that
focus on the distribution of the predictors.
The base R function sample can be used to create a completely random
sample of the data. The caret package has a function
createDataPartition that conducts data splits within groups of the
data.
For classification, this would mean sampling within the classes as to
preserve the distribution of the outcome in the training and test sets
For regression, the function determines the quartiles of the data set and
samples within those groups

Credit Data Set
For these data, let’s take a stratified random sample of 760 loans for
training.
> set.seed(8140)
> in_train <- createDataPartition(credit$Class, p = .75, list = FALSE)
> head(in_train)
Resample1
[1,]
[2,]
[3,]
[4,]
[5,]
[6,]
1
2
3
4
5
8
> train_data <- credit[ in_train,]
> test_data <- credit[-in_train,]

Estimating Performance
APM Ch. 5 and 11

Estimating Performance
Later, once you have a set of predictions, various metrics can be used to
evaluate performance.
For regression models:
R2 is very popular. In many complex models, the notion of the model
degrees of freedom is difficult. Unadjusted R2 can be used, but does
not penalize complexity
the root mean square error is a common metric for understanding
the performance
Spearman’s correlation may be applicable for models that are used to
rank samples
Of course, honest estimates of these statistics cannot be obtained by
predicting the same samples that were used to train the model.
A test set and/or resampling can provide good estimates.

Estimating Performance For Classification
For classification models:
overall accuracy can be used, but this may be problematic when the
classes are not balanced.
the Kappa statistic takes into account the expected error rate:
O −E
κ =
1 − E
where O is the observed accuracy and E is the expected accuracy
under chance agreement
For 2–class models, Receiver Operating Characteristic (ROC)
curves can be used to characterize model performance (more later)

A“ confusion matrix” is a cross–tabulation of the observed and predicted
classes
R functions for confusion matrices are in the e1071 package (the
classAgreement function), the caret package (confusionMatrix), the
mda (confusion) and others.
ROC curve functions are found in the pROC package (roc) ROCR
package (performance), the verification package (roc.area) and others.
We’ll use the confusionMatrix function and the pROC package later in
this class.

For 2–class classification models we might also be interested in:
Sensitivity: given that a result is truly an event, what is the
probability that the model willpredict an event results?
Specificity: given that a result is truly not an event, what is the
probability that the model willpredict a negative results?
(an “event” is really the event of interest)
These conditional probabilities are directly related to the false positive and
false negative rate of a method.
Unconditional probabilities (the positive–predictive values and negative–
predictive values) can be computed, but require an estimate of what the
overall event rate is in the population of interest (aka the prevalence)

For our example, let’s choose the event to be the loan being repaid:
# truly repaid predicted to be repaid
Sensitivity =
# truly repaid
# truly not repaid predicted to be not repaid
Specificity =
# truly not repaid
The caret package has functions called sensitivity and specificity

ROC Curve
With two classes the Receiver Operating Characteristic (ROC) curve can
be used to estimate performance using a combination of sensitivity and
specificity.
Given the probability of an event, many alternative cutoffs can be
evaluated (instead of just a 50% cutoff). For each cutoff, we can calculate
the sensitivity and specificity.
The ROC curve plots the sensitivity (eg. true positive rate) by one minus
specificity (eg. the false positive rate).
The area under the ROC curve is a common metric of performance.

ROC Curve
0.25 (Sp = 0.6, Sn = 0.9)
0.50 (Sp = 0.7, Sn = 0.8)
(Sp = 0.9, Sn = 0.6)
1.00 (Sp = 1.0, Sn = 0.0)
1.0 0.8 0.6 0.4 0.2 0.0
Specificity
Sensitivity
0.00.20.40.60.81.0
0.75
●
0
●
●
●
●

Over–Fitting and Model
Tuning
APM Ch. 4

Over–Fitting
Over–fitting occurs when a model inappropriately picks up on trends in the
training set that do not generalize to new samples.
When this occurs, assessments of the model based on the training set can
show good performance that does not reproduce in future samples.
Some models have specific “knobs” to control over-fitting
neighborhood size in nearest neighbor models is an example
the number if splits in a tree model
Often, poor choices for these parameters can result in over-fitting
For example, the next slide shows a data set with two predictors. We want
to be able to produce a line (i.e. decision boundary) that differentiates two
classes of data.
Two new points are to be predicted. A 5–nearest neighbor model is
illustrated.

K –Nearest Neighbors Classification
Class 1 Class 2
●0.6
0.4
0.2
0.0
0.0 0.2 0.4
Predictor A
0.6
PredictorB

Over–Fitting
On the next slide, two classification boundaries are shown for the a
different model type not yet discussed.
The difference in the two panels is solelydue to different choices in tuning
parameters.
One over–fits the training data.

Two Model Fits
0.2 0.4 0.6 0.8
0.8
0.6
0.4
0.2
0.2 0.4 0.6 0.8
Predictor A
PredictorB
Model #2Model #1

Characterizing Over–Fitting Using the Training Set
One obvious way to detect over–fitting is to use a test set. However,
repeated “looks” at the test set can also lead to over–fitting
Resampling the training samples allows us to know when we are making
poor choices for the values of these parameters (the test set is not used).
Resampling methods try to “inject variation” in the system to approximate
the model’s performance on future samples.
We’ll walk through several types of resampling methods for training set
samples.
See the two blog posts “Comparing Different Species of Cross-Validation”
at http://bit.ly/1yE0Ss5 and http://bit.ly/1zfoFj2

K –Fold Cross–Validation
Here, we randomly split the data into K distinct blocks of roughly equal
size.
We leave out the first block of data and fit a model.
This model is used to predict the held-out block
We continue this process until we’ve predicted all K held–out blocks
1
2
3
The final performance is based on the hold-out predictions
K is usually taken to be 5 or 10 and leave one out cross–validation has
each sample as a block
Repeated K –fold CV creates multiple versions of the folds and
aggregates the results (I prefer this method)

K –Fold Cross–Validation

In R
Many packages have cross–validation functions, but they are usually
limited to 10–fold CV.
caret has a general purpose function called train that has many
resampling methods for many models (more later).
caret has functions to produce samples splits for K –fold CV
(createFolds), multiple training/test splits (createDataPartition)
and bootstrap sampling (createResample).
Also, the base R function sample can be used to create completely
random splits or bootstrap samples

The Big Picture
We think that resampling willgive us honest estimates of future
performance, but there is still the issue of which model to select.
One algorithm to select models:
Define sets of model parameter values to evaluate;
for each parameter set do
for each resampling iteration do
Hold–out specific samples ;
Fit the model on the remainder;
Predict the hold–out samples;
end
Calculate the average performance across hold–out predictions
end
Determine the optimal parameter set;

K –Nearest Neighbors Classification
Class 1 Class 2
●0.6
0.4
0.2
0.0
0.0 0.2 0.4
Predictor A
0.6
PredictorB

The Big Picture – K NN Example
Using k–nearest neighbors as an example:
Randomly put samples into 10 distinct groups;
for k = 1, 3, 5, . . . , 21 do
for i = 1 . . . 10 do
Hold–out block i ;
Fit the model on the other 90%;
Predict the ith block and save results;
end
Calculate the average accuracy across the 10 hold–out sets of
predictions
end
Determine k based on the highest cross–validated accuracy;

The Big Picture – K NN Example
1.0
0.9
0.8
0.7
5 10 15 20
k
Accuracy

With a Different Set of Resamples
1.0
0.9
0.8
0.7
5 10 15 20
k
Accuracy

Data Pre–Processing
APM Ch. 3

Pre–Processing the Data
There are a wide variety of models in R. Some models have different
assumptions on the predictor data and may need to be pre–processed.
For example, methods that use the inverse of the predictor cross–product
matrix (i.e. (X tX )-1) may require the elimination of collinear predictors.
Others may need the predictors to be centered and/or scaled, etc.
If any data processing is required, it is a good idea to base these
calculations on the training set, then apply them to any data set used for
model building or prediction.

Pre–Processing the Data
Examples of of pre-processing operations:
centering and scaling
imputation of missing data
transformations of individual predictors
transformations of the groups of predictors, such as the
the "spatial-sign" transformation (i.e. xi = x/llxll)
feature extraction via PCA
�
�

Dummy Variables
Before pre-processing the data, there are a few predictors that are
categorical in nature.
For these, we would convert the values to binary dummy variables prior to
using them in numerical computations.
The core R function model.matrix can be used to do this.
If a categorical predictors has C levels, it would make C − 1 variables with
values 0 or 1 (one level would be omitted).

Dummy Variables
In the credit data, the Current Credit Quality predictor has C = 3 distinct
values:"no", "good_running,"and "bad_running"
For these data, the possible dummy variables are:
Dummy Variable Columns
Data Value no good_running bad_running
"no"
"good_running"
"bad_running"
1
0
0
0
1
0
0
0
1
For ordered categorical predictors, the default encoding is more complex.
See"The Basics of Encoding Categorical Data for Predictive Models"at
http://bit.ly/1CtXg0x

Dummy Variables
> alt_data <- model.matrix(Class ~ ., data = train_data)
> alt_data[1:4, 1:3]
(Intercept) Credit_Qualitygood_running Credit_Qualitybad_running
1
2
3
4
1
1
1
1
0
0
0
0
0
0
1
0
We can get rid of the intercept column and use this data.
However, we would want to apply this same transformation to new data
sets.
The caret function dummyVars has more options and can be applied to any
data
Note: using the formula method with models automatically handles this.

Dummy Variables
> dummy_info <- dummyVars(Class ~ ., data = train_data)
> dummy_info
Dummy Variable Object
Formula: Class ~ .
8 variables, 2 factors
Variables and levels will be separated by '.'
A less than full rank encoding is used
> train_dummies <- predict(dummy_info, newdata = train_data)
> train_dummies[1:4, 1:3]
Credit_Quality.no Credit_Quality.good_running Credit_Quality.bad_running
1
2
3
4
1
1
0
1
0
0
0
0
0
0
1
0
> test_dummies <- predict(dummy_info, newdata = test_data)

Dummy Variables and Model Functions
Most models are parameterized so that the predictors are required to be
numeric. Linear regression, for example, doesn’t know what to do with a
raw value of"green."
The primary convention in R is to convert factors to dummy variables
when a model uses the formula interface.
However, this is not always the case. Many models using trees or rules
(e.g. rpart, C5.0, randomForest, etc):
do not require numeric representations of the predictors
do not create dummy variables
Other notable exceptions are naive Bayes models and support vector
machines using string kernel functions.

Centering and Scaling
There are a few different functions for data processing in R:
scale in base R
ScaleAdv in pcaPP
stdize in pls
preProcess in caret
normalize in sparseLDA
The first three functions do simple centering and scaling. preProcess can
do a variety of techniques, so we’ll look at this in more detail.

Centering and Scaling
The input is a matrix or data frame of predictor data. Once the values are
calculated, the predict method can be used to do the actual data
transformations.
First, estimate the standardization parameters:
> pp_values <- preProcess(train_dummies, method = c("center", "scale"))
> pp_values
Call:
preProcess.default(x = train_dummies, method = c("center", "scale"))
Created from 750 samples and 9 variables
Pre-processing: centered, scaled
Apply them to the training and test sets:
> train_scaled <- predict(pp_values, newdata = train_dummies)
> test_scaled <- predict(pp_values, newdata = test_dummies)

Signal Extraction via PCA
Principal component analysis (PCA) can be used to create a (hopefully)
small subset of new predictors that capture most of the information in the
whole set.
The principal components are linear combinations of each individual
predictor and usually have not meaningful interpretation.
The components are created sequentially
the first captures the larges component of variation in the predictors
the second does the same for the leftover information, and so on
We can track how much of the variance is explained by the components
and select enough to have fidelity to the original data.

Signal Extraction via PCA
The advantages to this approach:
the components are all uncorrected to one another
a small number of predictors in the model can sometimes help
However...
this is not feature selection; all the predictors are still required
the components may not be correlated to the outcome

Signal Extraction via PCA in R
The base R function prcomp can be used to create the components.
preProcess can make the transformation and automatically retain the
number of components to account for some pre-specified amount of
information.
The predictors should be centered and scaled prior the PCA extraction.
preProcess will automatically do this even if you forget.

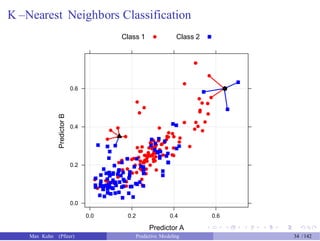
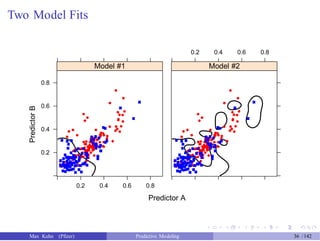
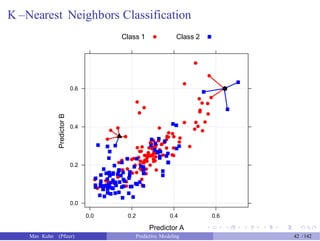
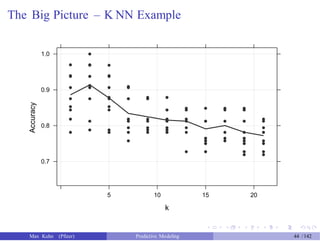
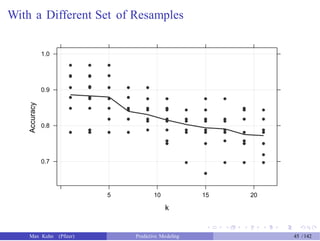
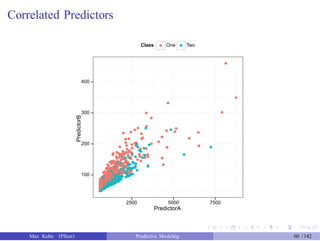
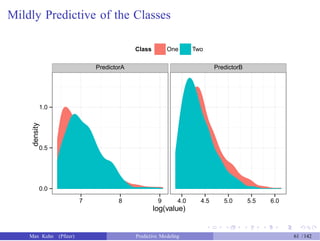
An Example
Another data set shows an nice example of PCA. There are two the
predictors and two classes:
> dim(example_train)
[1] 1009 3
> dim(example_test)
[1] 1010 3
> head(example_train)
PredictorA PredictorB Class
2
3
4
12
15
16
3278.726
1727.410
1194.932
1027.222
1035.608
1433.918
154.89876
84.56460
101.09107
68.71062
73.40559
79.47569
One
Two
One
Two
One
One

Correlated Predictors
Class One Two
400
300
200
100
2500 5000
PredictorA
7500
PredictorB

Mildly Predictive of the Classes
Class One Two
1.0
0.5
0.0
7 8 9 4.0 4.5 5.0 5.5 6.0
log(value)
density
PredictorA PredictorB

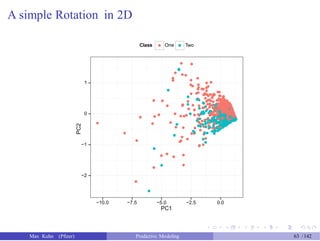
An Example
> pca_pp <- preProcess(example_train[, 1:2],
+
> pca_pp
method = "pca") # also added "center" and "scale"
Call:
preProcess.default(x = example_train[, 1:2], method = "pca")
Pre-processing: principal component signal extraction, scaled, centered
PCA needed 2 components to capture 95 percent of the variance
> train_pc <- predict(pca_pp, example_train[, 1:2])
> test_pc <- predict(pca_pp, example_test[, 1:2])
> head(test_pc, 4)
PC1
1 0.8420447
5 0.2189168
6 1.2074404
PC2
0.07284802
0.04568417
-0.21040558
7 1.1794578 -0.20980371

A simple Rotation in 2D
Class One Two
1
0
−1
−2
−10.0 −7.5 −5.0
PC1
−2.5 0.0
PC2

The First PC is Least Important Here
Class One Two
3
2
1
0
−2 −1 0 1 2 −2
value
−1 0 1 2
density
PC1 PC2

The Spatial Sign
The is another group transformation that can be effective when there are
significant outliers in the data.
For P predictors, the data are projected onto a unit sphere in P
dimensions.
Recall that our principal component values had very long tails. Let’s apply
the spatial sign after PCA extraction.
The predictors should be centered and scaled prior to this transformation
too.

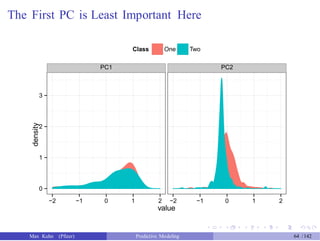
Adding Another Step
> pca_ss_pp <- preProcess(example_train[, 1:2],
+
> pca_ss_pp
method = c("pca", "spatialSign"))
Call:
preProcess.default(x = example_train[, 1:2], method = c("pca", "spatialSign"))
Pre-processing: principal component signal extraction, spatial
sign transformation, scaled, centered
PCA needed 2 components to capture 95 percent of the variance
> train_pc_ss <- predict(pca_ss_pp, example_train[, 1:2])
> test_pc_ss <- predict(pca_ss_pp, example_test[, 1:2])
> head(test_pc_ss, 4)
PC1
1 0.9962786
5 0.9789121
6 0.9851544
PC2
0.08619129
0.20428207
-0.17167058
7 0.9845449 -0.17513231

Projected onto a Unit Sphere
Class One Two
1.0
0.5
0.0
−0.5
−1.0
−1.0 −0.5 0.0
PC1
0.5 1.0
PC2

Pre–Processing and Resampling
To get honest estimates of performance, all data transformations should
be included within the cross-validation loop.
The would be especiallytrue for feature selection as well as pre-processing
techniques (e.g. imputation, PCA, etc)
One function considered later called train that can apply preProcess
within resampling loops.

Filtering Problematic Variables
Some models have computational issues if predictors have degenerate
distributions. For example, models that use X tX or it’s inverse might have
issues with
outliers
predictors with a single value (aka zero-variance predictors)
highly unbalanced distributions
Other models are insensitive to the characteristics of the predictor
distributions.
The caret functions findCorrelation and nearZeroVar can be used for
unsupervised filtering of predictors.

Feature Engineering
One of the most critical parts of the modeling process is feature
engineering; how should the predictors enter the model?
For example, two predictors might be more informative if they enter the
model as a ratio instead of as two main effects.
This requires an in-depth knowledge of the problem at hand and the
nuances of the data.
Also, like pre-processing, this is highly model dependent.

Example: Encoding Time and Date Data
Some applications have date or time data as predictors. How should we
encode this?
numerical day of the year along with the year?
categorical or ordinal factors for the day of the week, week, month, or
season, etc?
number of days from some reference date?
The answer depends on the type of model and the nature of the data.

I have found the lubridate package to be invaluable in these cases.
Let’s load some example dates from an existing RData file:
> day_values <- c("2015-05-10", "1970-11-04", "2002-03-04", "2006-01-13")
> class(day_values)
[1] "character"
> library(lubridate)
> days <- ymd(day_values)
> str(days)
POSIXct[1:4], format: "2015-05-10" "1970-11-04" "2002-03-04" "2006-01-13"

> day_of_week <- wday(days, label = TRUE)
> day_of_week
[1] Sun Wed Mon Fri
Levels: Sun < Mon < Tues < Wed < Thurs < Fri < Sat
> year(days)
[1] 2015 1970 2002 2006
> week(days)
[1] 19 45 10 2
> month(days, label = TRUE)
[1] May Nov Mar Jan
12 Levels: Jan < Feb < Mar < Apr < May < Jun < Jul < Aug < Sep < ... < Dec
> yday(days)
[1] 130 308 63 13

Classification
Models
APM Ch. 11-17

Classification Trees
A classification tree searches through each predictor to find a value of a
single variable that best splits the data into two groups.
typically, the best split minimizes impurity of the outcome in the
resulting data subsets.
For the two resulting groups, the process is repeated until a hierarchical
structure (a tree) is created.
in effect, trees partition the X space into rectangular sections that
assign a single value to samples within the rectangle.

An Example
There are many tree-based packages in R. The main package for fitting
single trees are rpart, RWeka, C50 and party. rpart fits the classical
"CART" models of Breiman et al (1984).
To obtain a shallow tree with rpart:
> library(rpart)
> rpart1 <- rpart(Class ~ .,
+
+
> rpart1
n= 750
data = train_data,
control = rpart.control(maxdepth = 2))
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 750 225 Good (0.7000000 0.3000000)
2) Credit_Quality=good_running 293 39 Good (0.8668942 0.1331058) *
3) Credit_Quality=no,bad_running 457 186 Good (0.5929978 0.4070022)
6) Loan_Duration< 31.5 366 129 Good (0.6475410 0.3524590) *
7) Loan_Duration>=31.5 91 34 Bad (0.3736264 0.6263736) *

Visualizing the Tree
The rpart package has functions plot.rpart and text.rpart to visualize
the final tree.
The partykit package also has enhanced plotting functions for recursive
partitioning. We can convert the rpart object to a new class called party
and plot it to see more in the terminal nodes:
> library(partykit)
> rpart1_plot <- as.party(rpart1)
> ## plot(rpart1_plot)

A Shallow rpart Tree Using the party Package
Credit_Quality
Loan_Duration
Node 2 (n = 293) Node 4 (n = 366) Node 5 (n = 91)
1 1 1
0.8
0.6
0.4
0.2
0
0.8
0.6
0.4
0.2
0
0.8
0.6
0.4
0.2
0
BadGood
BadGood
BadGood
31.531.5
3
no, bad_runninggood_running
1

Tree Fitting Process
Splitting would continue until some criterion for stopping is met, such as
the minimum number of observations in a node
The largest possible tree may over-fit and "pruning" is the process of
iteratively removing terminal nodes and watching the changes in
resampling performance (usually 10-fold CV)
There are many possible pruning paths: how many possible trees are there
with 6 terminal nodes?
Trees can be indexed by their maximum depth and the classical CART
methodology uses a cost-complexity parameter (Cp ) to determine best
tree depth

The Final Tree
Previously, we told rpart to use a maximum of two splits.
By default, rpart will conduct as many splits as possible, then use 10-fold
cross-validation to prune the tree.
Specifically, the "one SE" rule is used: estimate the standard error of
performance for each tree size then choose the simplest tree within one
standard error of the absolute best tree size.
> rpart_full <- rpart(Class ~ ., data = train_data)

The Final Tree
> rpart_full
n= 750
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 750 225 Good (0.7000000 0.3000000)
2) Credit_Quality=good_running 293 39 Good (0.8668942 0.1331058) *
3) Credit_Quality=no,bad_running 457 186 Good (0.5929978 0.4070022)
6) Loan_Duration< 31.5 366 129 Good (0.6475410 0.3524590)
12) Loan_Amount< 10975.5 359 122 Good (0.6601671 0.3398329)
24) Good_Payer>=0.5 323 100 Good (0.6904025 0.3095975)
48) Loan_Duration< 11.5 66 9 Good (0.8636364 0.1363636) *
49) Loan_Duration>=11.5 257 91 Good (0.6459144 0.3540856)
98) Loan_Amount>=1381.5 187 54 Good (0.7112299 0.2887701) *
99) Loan_Amount< 1381.5 70
198) Private_Loan>=0.5 38
199) Private_Loan< 0.5 32
33 Bad (0.4714286 0.5285714)
15 Good (0.6052632 0.3947368) *
10 Bad (0.3125000 0.6875000) *
25) Good_Payer< 0.5 36 14 Bad (0.3888889 0.6111111)
50) Loan_Duration>=16.5 23
100) Private_Loan>=0.5 11
101) Private_Loan< 0.5 12
51) Loan_Duration< 16.5 13
11 Good (0.5217391 0.4782609)
3 Good (0.7272727 0.2727273) *
4 Bad (0.3333333 0.6666667) *
2 Bad (0.1538462 0.8461538) *
13) Loan_Amount>=10975.5 7 0 Bad (0.0000000 1.0000000) *
7) Loan_Duration>=31.5 91 34 Bad (0.3736264 0.6263736)
14) Loan_Duration< 47.5 54 25 Bad (0.4629630 0.5370370)
28) Credit_Quality=bad_running 27 11 Good (0.5925926 0.4074074)
56) Loan_Amount< 7759 20 6 Good (0.7000000 0.3000000) *
57) Loan_Amount>=7759 7
29) Credit_Quality=no 27
15) Loan_Duration>=47.5 37
2 Bad (0.2857143 0.7142857) *
9 Bad (0.3333333 0.6666667) *
9 Bad (0.2432432 0.7567568) *

The Final rpart Tree
1
Credit_Quality
good_running no, bad_running
3
Loan_Duration
31.5 31.5
4 19
Loan_Amount Loan_Duration
10975.5 10975.5 47.5 47.5
5 20
Good_Payer Credit_Quality
0.5 0.5 bad_running no
6 13 21
Loan_Duration Loan_Duration Loan_Amount
11.5 11.5 16.5 16.5
8 14
Loan_Amount Private_Loan
1381.5 1381.5 7759 7759
10
Private_Loan 0.5 0.5
0.5 0.5
Node 2 (n = 293) Node 7 (n = 66) Node 9 (n = 187) Node 11 (n = 38) Node 12 (n = 32) Node 15 (n = 11) Node 16 (n = 12) Node 17 (n =
13)
Node 18 (n = 7) Node 22 (n = 20) Node 23 (n = 7) Node 24 (n = 27) Node 25 (n =
37)1 1 1 1 1 1 1 1 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0
0
BadGood
BadGood
BadGood
BadGood
BadGood
BadGood
BadGood
BadGood
BadGood
BadGood
BadGood
BadGood
BadGood
0.8
0.6
0.4
0.2
0.8
0.6
0.4
0.2
0.8
0.6
0.4
0.2
0.8
0.6
0.4
0.2
0.8
0.6
0.4
0.2
0.8
0.6
0.4
0.2
0.8
0.6
0.4
0.2
0.8
0.6
0.4
0.2
0.8
0.6
0.4
0.2
0.8
0.6
0.4
0.2
0.8
0.6
0.4
0.2
0.8
0.6
0.4
0.2
0.8
0.6
0.4
0.2

Test Set Results
> rpart_pred <- predict(rpart_full, newdata = test_data, type = "class")
> confusionMatrix(data = rpart_pred, reference = test_data$Class)
Confusion Matrix and Statistics
# requires 2 factor vectors
Reference
Prediction Good Bad
Good 163 49
Bad 12 26
Accuracy : 0.756
95% CI : (0.6979, 0.8079)
No Information Rate : 0.7
P-Value [Acc > NIR] : 0.02945
Kappa : 0.3237
Mcnemar's Test P-Value : 4.04e-06
Sensitivity : 0.9314
Specificity : 0.3467
Pos Pred Value : 0.7689
Neg Pred Value : 0.6842
Prevalence : 0.7000
Detection Rate : 0.6520
Detection Prevalence : 0.8480
Balanced Accuracy : 0.6390
'Positive' Class : Good

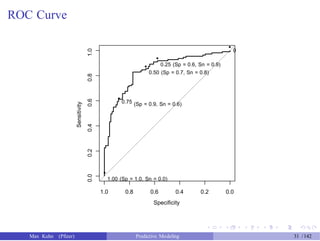
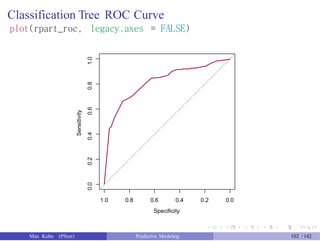
Creating the ROC Curve
The pROC package can be used to create ROC curves.
The function roc is used to capture the data and compute the ROC curve.
The functions plot.roc and auc.roc generate plot and area under the
curve, respectively.
> class_probs <- predict(rpart_full, newdata = test_data)
> head(class_probs, 3)
Good Bad
6 0.8636364 0.1363636
7 0.8636364 0.1363636
13 0.8636364 0.1363636
> library(pROC)
> ## The roc function assumes the *second* level is the one of
> ## interest, so we use the 'levels' argument to change the order.
> rpart_roc <- roc(response = test_data$Class, predictor = class_probs[, "Good"],
+ levels = rev(levels(test_data$Class)))
> ## Get the area under the ROC curve
> auc(rpart_roc)
Area under the curve: 0.7975

Tuning the Model
There are a few functions that can be used for this purpose in R.
the errorest function in the ipred package can be used to resample
a single model (e.g. a gbm model with a specific number of iterations
and tree depth)
the e1071 package has a function (tune) for five models that will
conduct resampling over a grid of tuning values.
caret has a similar function called train for over 183 models.
Different resampling methods are available as are custom performance
metrics and facilities for parallel processing.

The train Function
The basic syntax for the function is:
> train(formula, data, method)
Looking at ?train, using method =
over Cp , so we can use:
"rpart" can be used to tune a tree
> train(Class ~ ., data = train_data, method = "rpart")
We’ll add a bit of customization too.

The train Function
By default, the function willtune over 3 values of the tuning parameter
(Cp for this model).
For rpart, the train function determines the distinct number of values of
Cp for the data.
The tuneLength function can be used to evaluate a broader set of models:
>
+
+
rpart_tune <- train(Class ~ ., data =
method = "rpart",
tuneLength = 9)
train_data,

The train Function
The default resampling scheme is the bootstrap. Let’s use 10-fold
cross-validation instead.
To do this, there is a control function that handles some of the optional
arguments.
To use five repeats of 10-fold cross-validation, we would use
>
>
+
+
+
cv_ctrl <-
rpart_tune
trainControl(method = "repeatedcv", repeats = 5)
<- train(Class ~ ., data = train_data,
method = "rpart",
tuneLength = 9,
trControl = cv_ctrl)

The train Function
Also, the default CART algorithm uses overall accuracy and the one
standard-error rule to prune the tree.
We might want to choose the tree complexity based on the largest
absolute area under the ROC curve.
A custom performance function can be passed to train. The package has
one that calculates the ROC curve, sensitivity and specificity called . For
example:
> twoClassSummary(fakeData)
ROC Sens Spec
0.5020 0.1145 0.8827

The train Function
We can pass the twoClassSummary function in through trainControl.
However, to calculate the ROC curve, we need the model to predict the
class probabilities. The classProbs option will also do this:
Finally, we tell the function to optimize the area under the ROC curve
using the metric argument:
>
+
+
>
>
+
+
+
+
cv_ctrl <- trainControl(method = "repeatedcv", repeats = 5,
summaryFunction = twoClassSummary,
classProbs = TRUE)
set.seed(1735)
rpart_tune <- train(Class ~ ., data = train_data,
method = "rpart",
tuneLength = 9,
metric = "ROC",

Digression – Parallel Processing
Since we are fitting a lot of independent models over different tuning
parameters and sampled data sets, there is no reason to do these
sequentially.
R has many facilities for splitting computations up onto multiple cores or
machines
See Tierney et al (2009, Journal of Statistical Software) for a recent
review of these methods

foreach and caret
To loop through the models and data sets, caret uses the foreach package,
which parallelizes for loops.
foreach has a number of parallel backends which allow various technologies
to be used in conjunction with the package.
On CRAN, these are the doSomething packages, such as doMC, doMPI,
doSMP and others.
For example, doMC uses the multicore package, which forks processes to
split computations (for unix and OS X). doParallel works well for Windows
(I’m told)

foreach and caret
To use parallel processing in caret, no changes are needed when calling
train.
The parallel technology must be registered with foreach prior to calling
train.
For multicore
> library(doMC)
> registerDoMC(cores = 2)

Training Time (min)
50 bootstraps of a SVM model with 1000 samples and 400 predictors and
the multicore package
500
400
300
200
100
2 4 6 8 10 12
cores
min
●
●
●
● ●
●
●
●
●
●
●
●
●

Speed–Up
5
4
3
2 ●
1 ●
2 4 6 8 10 12
cores
SpeedUp
●
●
●
●
●
●
●
●
●
●
●

train Results
> rpart_tune
CART
750 samples
7 predictor
2 classes: 'Good', 'Bad'
No pre-processing
Resampling: Cross-Validated (10 fold, repeated 5 times)
Summary of sample sizes: 675, 675, 674, 674, 676, 675, ...
Resampling results across tuning parameters:
cp
0.00000
0.00222
0.00444
0.00778
0.00889
0.01111
0.01778
0.03333
0.05111
ROC
0.697
0.696
0.695
0.695
0.695
0.693
0.646
0.554
0.507
Sens
0.835
0.841
0.848
0.864
0.863
0.861
0.877
0.912
0.954
Spec
0.4447
0.4367
0.4163
0.3772
0.3817
0.3801
0.3529
0.2591
0.0996
ROC SD
0.0750
0.0744
0.0708
0.0877
0.0898
0.0959
0.1487
0.1876
0.1149
Sens SD
0.0488
0.0480
0.0467
0.0433
0.0455
0.0442
0.0526
0.0505
0.0510
Spec SD
0.115
0.110
0.102
0.114
0.119
0.127
0.101
0.104
0.106
ROC was used to select the optimal model using the largest value.
The final value used for the model was cp = 0.

Working With the train Object
There are a few methods of interest:
plot.train or ggplot.train can be used to plot the resampling
profiles across the different models
print.train shows a textual description of the results
predict.train can be used to predict new samples
there are a few others that we’ll mention shortly.
Additionally, the final model fit (i.e. the model with the best resampling
results) is in a sub-object called finalModel.
So in our example, rpart_tune is of class train and the object
rpart_tune$finalModel is of class rpart.
Let’s look at what the plot method does.

Resampled ROC Profile
ggplot(rpart_tune)
● ● ●
0.55
ROC(RepeatedCross−Validation)
● ● ●
0.70
0.65 ●
0.60
●
●
0.50
0.00 0.01 0.02 0.03 0.04 0.05
Complexity Parameter

Predicting New Samples
There are at least two ways to get predictions from a train object:
predict(rpart_tune$finalModel, newdata, type = "class")
predict(rpart_tune, newdata)
The first method uses predict.rpart, but is not preferred if using train.
predict.train does the same thing, but automatically uses the number
of trees that were selected using the train function.

Test Set Results
> rpart_pred2 <- predict(rpart_tune, newdata = test_data)
> confusionMatrix(rpart_pred2, test_data$Class)
Reference
Prediction Good Bad
Good 161 47
Bad 14 28
Accuracy : 0.756
95% CI : (0.6979, 0.8079)
Kappa : 0.3355
Prevalence : 0.7000

Predicting Class Probabilities
predict.train has an argument type that can be used to get predicted
class probabilities for different models:
> rpart_probs <- predict(rpart_tune, newdata = test_data, type = "prob")
> head(rpart_probs, n = 4)
Good Bad
6 0.8636364 0.1363636
7 0.8636364 0.1363636
13 0.8636364 0.1363636
16 0.8636364 0.1363636
> rpart_roc <- roc(response = test_data$Class, predictor = rpart_probs[, "Good"],
+
> auc(rpart_roc)
levels = rev(levels(test_data$Class)))

Classification Tree ROC Curve
plot(rpart_roc, legacy.axes = FALSE)
1.0 0.8 0.6 0.4 0.2 0.0
Specificity
Sensitivity
0.00.20.40.60.81.0

Pros and Cons of Single Trees
Trees can be computed very quickly and have simple interpretations.
Also, they have built-in feature selection; if a predictor was not used in any
split, the model is completely independent of that data.
Unfortunately, trees do not usually have optimal performance when
compared to other methods.
Also, small changes in the data can drastically affect the structure of a
tree.
This last point has been exploited to improve the performance of trees via
ensemble methods where many trees are fit and predictions are aggregated
across the trees. Examples are bagging, boosting and random forests.

Boosted Trees (Original“ adaBoost” Algorithm)
A method to "boost" weak learning algorithms (e.g. single trees) into
strong learning algorithms.
Boosted trees try to improve the model fit over different trees by
considering past fits (not unlike iteratively reweighted least squares)
The basic adaBoost algorithm:
Initialize equal weights per sample;
for j = 1 . . . M iterations do
Fit a classification tree using sample weights (denote the model
equation as fj (x));
forall the misclassified samples do
increase sample weight
end
Save a "stage-weight"(βj ) based on the performance of the current
model;
end

Boosted Trees (Original“ adaBoost” Algorithm)
In this formulation, the categorical response yi is coded as either {−1, 1}
and the model fj (x ) produces values of {−1, 1}.
The final prediction is obtained by first predicting using all M trees, then
weighting each prediction
M
1
f (x) =
X
βj fj (x)
M j =1
where fj is the j th tree fit and βj is the stage weight for that tree.
The final class is determined by the sign of the model prediction.
In English: the final prediction is a weighted average of each tree’s
prediction. The weights are based on quality of each tree.

Statistical Approaches to Boosting
The original algorithm was developed outside of statistical theory.
Statisticians discovered that the basic boosting algorithm was very similar
to gradient-based steepest decent methods, such as Newton’s method.
Based on their observations, a new class of boosted tree models were
proposed and are generally referred to as"gradient boosting" methods.

Boosted Trees Parameters
Most implementations of boosting have three tuning parameters:
number of iterations (i.e. trees)
complexity of the tree (i.e. number of splits)
learning rate (aka. "shrinkage"): how quickly the algorithm adapts
the minimum number of samples in a terminal node
Boosting functions for trees in R: gbm in the gbm package, ada in ada,
blackboost in mboost and C5.0 in the C50 package.

Using the gbm Package
The gbm function in the gbm package can be used to fit the model, then
predict.gbm and other functions are used to predict and evaluate the
model.
>
>
>
>
>
>
>
>
+
+
+
+
+
+
library(gbm)
# The gbm function does not accept factor response values so
# will make a copy and modify the result variable
for_gbm <- train_data
for_gbm$Class <- ifelse(for_gbm$Class == "Good", 1, 0)
set.seed(10)
gbm_fit <- gbm(formula = Class ~ ., # Try all predictors
distribution = "bernoulli", # For classification
data = for_gbm,
n.trees = 100,
interaction.depth = 1,
shrinkage = 0.1,
verbose = FALSE)
# 100 boosting iterations
# How many splits in each tree
# learning rate
# Do not print the details

gbm Predictions
We need to tell the predict method how many trees to use (let’s just pick
500).
Also, it does not predict the actual class. We’ll get the class probability
and do the conversion.
> gbm_pred <- predict(gbm_fit, newdata = test_data, n.trees = 100,
+
+
> head(gbm_pred)
## This calculates the class probs
type = "response")
[1] 0.6803420 0.7628453 0.6882552 0.8262940 0.8861083 0.7280930
> gbm_pred <- factor(ifelse(gbm_pred > .5, "Good", "Bad"),
+
> head(gbm_pred)
levels = c("Good", "Bad"))
[1] Good Good Good Good Good Good
Levels: Good Bad

Test Set Results
> confusionMatrix(gbm_pred, test_data$Class)
Reference
Prediction Good Bad
Good 166 51
Bad 9 24
Accuracy : 0.76
95% CI : (0.7021, 0.8116)
Kappa : 0.3197
Prevalence : 0.7000

Model Tuning using train
We can fit a series of boosted trees with different specifications and use
resampling to understand which one is most appropriate.
For example, we can define a grid of 152 tuning parameter combinaitons:
number of trees: 100 to 1000 by 50
tree depth: 1 to 7 by 2
learning rate: 0.0001 and 0.01
minimum sample size of 10 (the default)
In R:
> gbm_grid <- expand.grid(interaction.depth = seq(1, 7, by = 2),
+
+
+
n.trees = seq(100, 1000, by = 50),
shrinkage = c(0.0001, 0.01),
n.minobsinnode = 10)
We can use this grid to define exactly what models are evaluated by
train. A list of model parameter names can be found using ?train.

Another Digression – The Ellipses
R has a great feature known as the ellipses(aka "three dots") where an
arbitrary number of function arguments can be pass through nested
function calls. For example:
> average <- function(dat, ...) mean(dat, ...)
> names(formals(mean.default))
[1] "x" "trim" "na.rm" "..."
> average(dat = c(1:10, 100))
[1] 14.09091
> average(dat = c(1:10, 100), trim = .1)
[1] 6
train is structured to take full advantage of this so that arguments can
be passed to the underlying model function (e.g. rpart, gbm) when calling
the train function.

Model Tuning using train
>
>
+
+
+
+
+
+
+
+
set.seed(1735)
gbm_tune <- train(Class ~ ., data = train_data,
method = "gbm",
metric = "ROC",
# Use a custom grid of tuning parameters
tuneGrid = gbm_grid,
trControl = cv_ctrl,
# Remember the 'three dots' discussed previously?
# This options is directly passed to the gbm function.
verbose = FALSE)

Boosted Tree Results
> gbm_tune
Stochastic Gradient Boosting
750 samples
7 predictor
No pre-processing
shrinkage
1e-04
1e-04
1e-04
1e-04
:
1e-02
1e-02
1e-02
interaction.depth
1
1
1
1
:
7
7
7
n.trees
100
150
200
250
:
900
950
1000
ROC
0.608
0.661
0.661
0.681
:
0.733
0.731
0.729
Sens
1.000
1.000
1.000
1.000
:
0.880
0.876
0.877
Spec
0.00000
0.00000
0.00000
0.00000
:
0.42518
0.42783
0.43047
Tuning parameter 'n.minobsinnode' was held constant at a value of 10
The final values used for the model were n.trees = 450, interaction.depth =
3, shrinkage = 0.01 and n.minobsinnode = 10.

Boosted Tree ROC Profile
ggplot(gbm_tune)
0.750
●
●
●
●
0.725
Max Tree Depth
0.700
1
3
5
7
0.675
●
0.650
0.625 ●
250 500 750 1000 250 500 750 1000
# Boosting Iterations
●
0.001 0.010
●
●
●
●
● ●
●● ●
●
●
● ●
●
●
●
● ●
●
●
●
● ●
● ● ●
●
●
●
●
●
●

Test Set Results
> gbm_pred <- predict(gbm_tune, newdata = test_data) # Magic!
> confusionMatrix(gbm_pred, test_data$Class)
Reference
Prediction Good Bad
Good 167 52
Bad 8 23
Accuracy : 0.76
95% CI : (0.7021, 0.8116)
Kappa : 0.3135
Prevalence : 0.7000

GBM Probabilities
> gbm_probs <- predict(gbm_tune, newdata = test_data, type = "prob")
> head(gbm_probs)
Good Bad
1 0.7559353 0.2440647
2 0.8336368 0.1663632
3 0.7846890 0.2153110
4 0.8455947 0.1544053
5 0.8454949 0.1545051
6 0.6093760 0.3906240

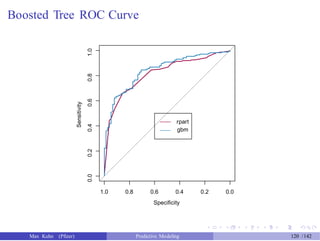
Boosted Tree ROC Curve
> gbm_roc <- roc(response = test_data$Class, predictor = gbm_probs[, "Good"],
+
> auc(rpart_roc)
> auc(gbm_roc)
> plot(rpart_roc, col = "#9E0142", legacy.axes = FALSE)
> plot(gbm_roc, col = "#3288BD", legacy.axes = FALSE, add = TRUE)
> legend(.6, .5, legend = c("rpart", "gbm"),
+
+
lty = c(1, 1),
col = c("#9E0142", "#3288BD"))

Boosted Tree ROC Curve
1.0 0.8 0.6 0.4 0.2 0.0
Specificity
Sensitivity
0.00.20.40.60.81.0
rpart
gbm

Support Vector Machines for
Classification
APM Sect 13.4

Support Vector Machines (SVM)
This is a class of powerful and very flexible models.
SVMs for classification use a completely different objective function called
the margin.
Suppose a hypothetical situation: a dataset of two predictors and we are
trying to predict the correct class (two possible classes).
Let’s further suppose that these two predictors completely separate the
classes

Support Vector Machines
−4 −2 0 2 4
Predictor 1
Predictor2
−4−2024

There are an infinite number of straight lines that we can use to separate
these two groups. Some must be better than others...
The margin is a defined by equally spaced boundaries on each side of the
line.
To maximize the margin, we try to make it as large as possible without
capturing any samples.
As the margin increases, the solution becomes more robust.
SVMs determine the slope and intercept of the line which maximizes the
margin.

Maximizing the Margin
−4 −2 0 2 4
Predictor 1
Predictor2
−4−2024

SVM Prediction Function
Suppose our two classes are coded as -1 or 1.
The SVM model estimates n parameters ("1 . . . "n ) for the model.
Regularization is used to avoid saturated models (more on that in a
minute).
For a new point u, the model predicts:
n
f (u) = β0 +
"
"'i'xtu '
'=1
The decision rule would predict class #1 if f (u ) > 0 and class #2
otherwise.
Data points that are support vectors have "' =0, so the prediction
equation is only affected by the support vectors.

When the classes overlap, points are allowed within the margin. The
number of points is controlled by a cost parameter.
The points that are within the margin (or on it’s boundary) are the
support vectors
Consequences of the fact that the prediction function only uses the
support vectors:
the prediction equation is more compact and efficient
the model may be more robust to outliers

The Kernel Trick
You may have noticed that the prediction function was a function of an
inner product between two samples vectors (xtu). It turns out that this'
opens up some new possibilities.
Nonlinear class boundaries can be computed using the "kernel trick".
The predictor space can be expanded by adding nonlinear functions in x.
These functions, which must satisfy specific mathematical criteria, include
common functions:
Polynomial : K (x , u) = (1 + x tu)p
r
-a
2
1
(x - u)2
Radial basis function : K (x, u) = exp
We don’t need to store the extra dimensions; these functions can be
computed quickly.

SVM Regularization
As previouslydiscussed, SVMs also include a regularization parameter that
controls how much the regression line can adapt to the data smaller values
result in more linear (i.e. flat) surfaces
This parameter is generally referred to as"Cost"
If the cost parameter is large, there is a significant penalty for having
samples within the margin ⇒ the boundary becomes very flexible.
Tuning the cost parameter, as well as any kernel parameters, becomes very
important as these models have the ability to greatly over-fit the training
data.
(animation)

SVM Models in R
There are several packages that include SVM models:
e1071 has the function svm for classification (2+ classes) and
regression with 4 kernel functions
klaR has svmlight which is an interface to the C library of the same
name. It can do classification and regression with 4 kernel functions
(or user defined functions)
svmpath has an efficient function for computing 2-class models
(including 2 kernel functions)
kernlab contains ksvm for classification and regression with 9 built-in
kernel functions. Additional kernel function classes can be written.
Also, ksvm can be used for text mining with the tm package.
Personally, I prefer kernlab because it is the most general and contains
other kernel method functions (e1071 is probably the most popular).

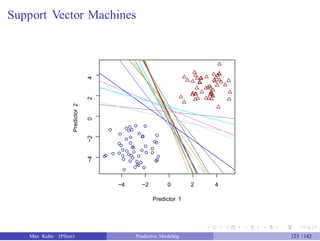
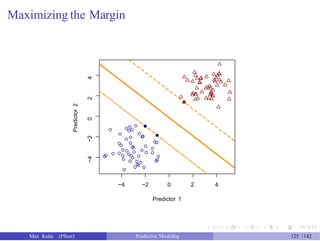
Tuning SVM Models
We need to come up with reasonable choices for the cost parameter and
any other parameters associated with the kernel, such as
polynomial degree for the polynomial kernel
a, the scale parameter for radial basis functions (RBF)
We’ll focus on RBF kernel models here, so we have two tuning parameters.
However, there is a potential shortcut for RBF kernels. Reasonable values
of a can be derived from elements of the kernel matrix of the training set.
The manual for the sigest function in kernlab has "The estimation [for a]
is based upon the 0.1 and 0.9 quantile of lx - x tl2."
Anecdotally, we have found that the mid-point between these two
numbers can provide a good estimate for this tuning parameter. This
leaves only the cost function for tuning.

SVM Example
We can tune the SVM model over the cost parameter.
>
>
+
+
+
+
+
+
+
+
+
set.seed(1735)
svm_tune <- train(Class ~ ., data = train_data,
method = "svmRadial",
# The default grid of cost parameters go from 2^-2,
# 0.5, 1, ...
# We'll fit 10 values in that sequence via the tuneLength
# argument.
tuneLength = 10,
preProc = c("center", "scale"),
metric = "ROC",

SVM Example
> svm_tune
Support Vector Machines with Radial Basis Function Kernel
750 samples
7 predictor
Pre-processing: centered, scaled
C ROC
0.719
0.719
0.719
0.717
0.710
0.691
0.675
0.667
0.655
0.644
Sens
0.914
0.923
0.924
0.924
0.925
0.928
0.934
0.948
0.958
0.966
Spec
0.308
0.308
0.295
0.278
0.265
0.233
0.208
0.174
0.143
0.112
ROC SD
0.0726
0.0719
0.0732
0.0726
0.0757
0.0768
0.0780
0.0771
0.0783
0.0757
Sens SD
0.0443
0.0414
0.0429
0.0429
0.0464
0.0457
0.0413
0.0354
0.0369
0.0291
Spec SD
0.0915
0.0934
0.0926
0.0982
0.0967
0.1028
0.0883
0.0934
0.0823
0.0681
0.25
0.50
1.00
2.00
4.00
8.00
16.00
32.00
64.00
128.00
Tuning parameter 'sigma' was held constant at a value of 0.11402
The final values used for the model were sigma = 0.114 and C = 0.5.

SVM Example
> svm_tune$finalModel
Support Vector Machine object of class "ksvm"
SV type: C-svc (classification)
parameter : cost C = 0.5
Gaussian Radial Basis kernel function.
Hyperparameter : sigma = 0.114020038085962
Number of Support Vectors : 458
Objective Function Value : -202.0199
Training error : 0.230667
Probability model included.
458 training data points (out of 750 samples) were used as support vectors.

SVM ROC Profile
ggplot(svm_tune) + scale_x_log10()
0.72
●
0.70
0.68
0.66
0.64
1 10 100
Cost
● ● ● ●
●
●
●
●
●

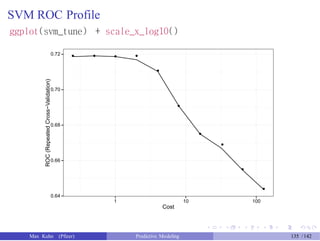
Test Set Results
> svm_pred <- predict(svm_tune, newdata = test_data)
> confusionMatrix(svm_pred, test_data$Class)
Reference
Prediction Good Bad
Good 165 49
Bad 10 26
Accuracy : 0.764
95% CI : (0.7064, 0.8152)
Kappa : 0.34
Prevalence : 0.7000

SVM Probability Estimates
> svm_probs <- predict(svm_tune, newdata = test_data, type = "prob")
> head(svm_probs)
Good Bad
1 0.8008819 0.1991181
2 0.8064645 0.1935355
3 0.8103000 0.1897000
4 0.7944448 0.2055552
5 0.6722484 0.3277516
6 0.7202097 0.2797903

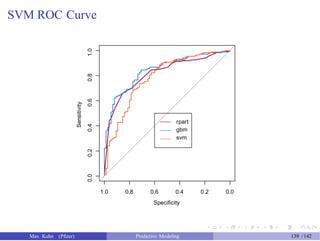
SVM ROC Curve
> svm_roc <- roc(response = test_data$Class, predictor = svm_probs[, "Good"],
+
> auc(rpart_roc)
> auc(gbm_roc)
> auc(svm_roc)
> plot(rpart_roc, col = "#9E0142", legacy.axes = FALSE)
> plot(gbm_roc, col = "#3288BD", legacy.axes = FALSE, add = TRUE)
> plot(svm_roc, col = "#F46D43", legacy.axes = FALSE, add = TRUE)
> legend(.6, .5, legend = c("rpart", "gbm", "svm"),
+
+
lty = c(1, 1, 1),
col = c("#9E0142", "#3288BD", "#F46D43"))

SVM ROC Curve
1.0 0.8 0.6 0.4 0.2 0.0
Specificity
Sensitivity
0.00.20.40.60.81.0
rpart
gbm
svm

Other Functions and Classes
bag: a genereal bagging function
upSample, downSample: functions for class imbalances
predictors: class for determining which predictors are included in
the prediction equations (e.g. rpart, earth, lars models)
varImp: classes for assessing the aggregate effect of a predictor on
the model equations
lift: creating lift/gain charts

Other Functions and Classes
knnreg: nearest-neighbor regression
plsda, splsda: PLS discriminant analysis
icr: independent component regression
pcaNNet: nnet:::nnet with automatic PCA pre-processing step
bagEarth, bagFDA: bagging with MARS and FDA models
maxDissim: a function for maximum dissimilarity sampling
rfe, sbf, gabf, sabf: classes/frameworks for recursive feature
selection (RFE), univariate filters, genetic algrithms, simulated
annealing feature selection methods
featurePlot: a wrapper for several lattice functions

Session Info
R version 3.1.3 (2015-03-09), x86_64-apple-darwin10.8.0
Base packages: base, datasets, graphics, grDevices, grid, methods, parallel,
splines, stats, tcltk, utils
Other packages: C50 0.1.0-24, caret 6.0-47, class 7.3-12, ctv 0.8-1,
doMC 1.3.3, Fahrmeir 2012.04-0, foreach 1.4.2, Formula 1.2-0, gbm 2.1.1,
ggplot2 1.0.1, Hmisc 3.15-0, iterators 1.0.7, kernlab 0.9-20, knitr 1.9,
lattice 0.20-30, lubridate 1.3.3, MASS 7.3-40, mlbench 2.1-1,
odfWeave 0.8.4, partykit 1.0-0, plyr 1.8.1, pROC 1.8, reshape2 1.4.1,
rpart 4.1-9, survival 2.38-1, XML 3.98-1.1
Loaded via a namespace (and not attached): acepack 1.3-3.3,
BradleyTerry2 1.0-6, brglm 0.5-9, car 2.0-25, cluster 2.0.1, codetools 0.2-10,
colorspace 1.2-6, compiler 3.1.3, digest 0.6.8, e1071 1.6-4, evaluate 0.5.5,
foreign 0.8-63, formatR 1.0, gtable 0.1.2, gtools 3.4.2, highr 0.4,
labeling 0.3, latticeExtra 0.6-26, lme4 1.1-7, Matrix 1.2-0, memoise 0.2.1,
mgcv 1.8-6, minqa 1.2.4, munsell 0.4.2, nlme 3.1-120, nloptr 1.0.4,
nnet 7.3-9, pbkrtest 0.4-2, proto 0.3-10, quantreg 5.11, RColorBrewer 1.1-2,
Rcpp 0.11.5, scales 0.2.4, SparseM 1.6, stringr 0.6.2, tools 3.1.3

Predictive Modeling Workshop

More Related Content

What's hot

Similar to Predictive Modeling Workshop

More from odsc

Recently uploaded

Predictive Modeling Workshop