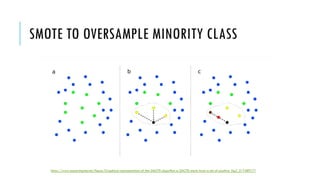
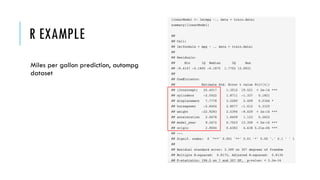
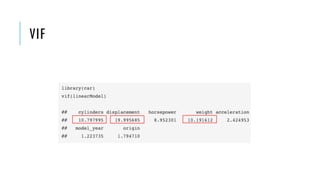
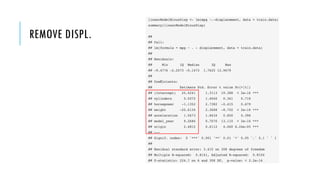
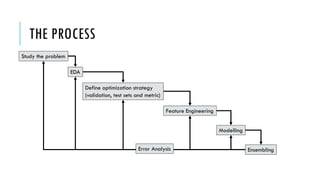
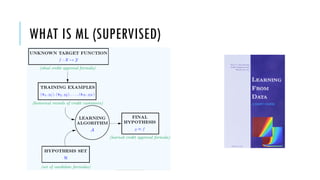
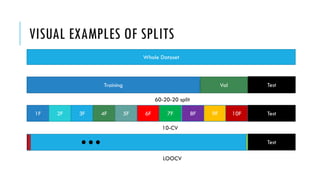
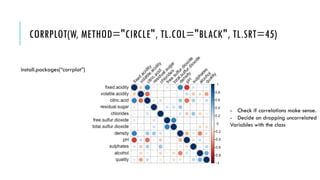
The document outlines simple rules for building robust machine learning models, emphasizing the importance of splitting data into training, validation, and test sets, and ensuring each set is representative of future data distributions. It discusses various metrics for model evaluation, the significance of exploratory data analysis, and the impact of data preprocessing on model performance. Additionally, it covers guidelines for selecting appropriate algorithms, tuning hyperparameters, and conducting experiments efficiently.

1. SIMPLE RULES FOR BUILDING
ROBUST MACHINE LEARNING MODELSWITH EXAMPLES IN R
Kyriakos Chatzidimitriou
Research Fellow, Aristotle University of Thessaloniki
PhD in Electrical and Computer Engineering
kyrcha@issel.ee.auth.gr
AMA Call
Early Career and Engagement IG

2. ABOUT ME
• Born in 1978
• 1997-2003, Diploma in Electrical and Computer Engineering, AUTH, GREECE
• 2003-2004, Worked as a developer
• 2004-2006, MSc in Computer Science, CSU, USA
• 2006-2007, Greek Army
• 2007-2012, PhD, AUTH, GREECE
• Reinforcement learning and evolutionary computing mechanisms for autonomous agents
• 2013-Now, Research Fellow, ECE, AUTH
• 2017-Now, co-founder, manager and full stack developer of Cyclopt P.C.
• Spin-off company of AUTH focusing on software analytics

3. GENERAL CAREER ADVICE
Life is hard and full of problems.
No point thus in meaningless suffering J
To be happy and for the problems
you can choose, choose those that
you like solving.
By working on the 10K hour of
more…
…you will be too good to be ignored
and you will achieve that by focusing on
deep work and working on difficult
problems
Positive feedback loop,
where good things happen

4. WHAT IS ML (SUPERVISED)

5. WHAT AM I WORKING ON ML WISE
Deep website aesthetics
AutoML
Continuous Implicit Authentication
Formatting or linting errors

6. SIMPLE RULE 1: SPLIT YOU DATA IN THREE

7. GREEK SONG
• «Δεν υπάρχει ευτυχία, που να κόβεται στα τρία…» – “There is no happiness split in
three…”
• Not true for ML

8. THE THREE SETS
•Training set — Data on which the learning algorithms runs
•Validation set — Used for making decisions: tuning parameters,
selecting features, model complexity
­Test set — Only used for evaluating performance
­ Else data snooping

9. DO NOT TAKE ANY DECISIONS ON THE TEST SET
- Do not use it for selecting ANYTHING!
- Rely on the validation score only

10. VISUAL EXAMPLES OF SPLITS
Whole Dataset
Training Val Test
1F 2F 3F 4F 5F 6F 7F 8F 9F 10F Test
Test
60-20-20 split
10-CV
LOOCV

11. R EXAMPLE
k = 5
results <- numeric(k)
ind <- sample(2, nrow(iris), replace=T, prob=c(0.8, 0.2))
trainval <- iris[ind==1,]
test <- iris[ind !=1,]
cv <- sample(rep(1:k, length.out=nrow(trainval)))
for(i in 1:k) {
trainData <- trainval[cv != i,]
valData <- trainval[cv == i,]
model <- naiveBayes(Species ~ ., data=trainData, laplace = 0)
pred <- predict(model, valData)
results[i] <- Accuracy(pred, valData$Species)
}
print(mean(results))
# after finding the best laplace
finalmodel <- naiveBayes(Species ~ ., data=trainval,
laplace = 0)
pred <- predict(finalmodel, test)
print(Accuracy(pred, test$Species))
Validation - 0.95 vs. 0.91 - Test

12. SIMPLE RULE 2: SPLIT YOUR DATA IN THREE,
CORRECTLY

13. 1948 US ELECTIONS
1948, Truman vs. Dewey
Newspaper made a phone poll the previous day
Most of Dewey supporters had phones those days

14. RULE
• Choose validation and test sets to reflect the data you expect to see in the future
• Ideally performance in validation and test sets should be the same
• Example: Let’s say validation set performance is super and test set performance is so
and so
• If from the same distribution:
• You had overfitted the validation set
• If from different distributions
• You had overfitted the validation set
• Test set is harder
• Test set is different

15. EXAMPLE OF STRATIFIED CV IN R
iris$Species <- as.numeric(iris$Species)
folds <- createFolds(iris$Species, list=FALSE)
#caret
iris$folds <- folds
ddply(iris, 'folds', summarise, prop=mean(Species))
non_strat_folds <- sample(rep(1:10,
length.out=nrow(iris)))
iris$non_strat_folds <- non_strat_folds
ddply(iris, 'non_strat_folds', summarise,
prop=mean(Species))
Things will be (much) worse if the distribution is more skewed

16. SIMPLE RULE 3: DATASET SIZE IS IMPORTANT

17. SIZE HEURISTICS
• #1 Good validation set sizes are between 1000 and 10K
• #2 For the training set have at least 10x the VC-dimension
• For a NN is roughly equal to the number of weights
• #3 Popular heuristic for test size should be 30%, less for large problems
• #4 If you have more data, put them in the validation set to reduce overfitting
• #5 The validation set should be large enough to detect differences between
algorithms
• For distinguishing between classifier A with 90% accuracy and B with 90.1% accuracy then 100
validation examples will not do it.

18. FINANCIAL IMPACT OF 0.1%
Before
10,000,000 searches
1% CTR
100,000 visitors
1% conversion
1,000 purchases
$100
$100,000
After
10,000,000 searches
1.1% CTR
110,000 visitors
1.1% conversion
1,210 purchases
$100
$121,000
+$21,000
Bid
Prediction
Adaptive Content

19. LEARNING
CURVES AS A
TOOL

20. SIMPLE RULE 4: CHOOSE ONE METRIC

21. DIFFERENT METRIC FOR DIFFERENT NEEDS
• The one metrics allows faster iterations and focus
• Are your classes balanced? Use accuracy
• Are your classes imbalanced? Use the F1-score
• Are you doing multilabel classification? Use for example macro-averaged accuracy
• 𝐵"#$%& =
(
)
∑+,(
)
𝐵(𝑇𝑃+, 𝐹𝑃+, 𝑇𝑁+, 𝐹𝑁+)
• B is a binary evaluation metric like Accuracy =
:;<=:><
:;<=?;<=:><=?><
• The application dictates the metric
• Continuous Implicit Authentication: Equal Error Rate
• Combines two metrics: False Acceptance Rate and False Rejection Rate
• Interested both in preventing impostors but also allowing legitimate users

22. SIMPLE RULE 5: ALWAYS DO YOUR EDA

23. THE QUESTION TO ASK IN EXPLORATORY DATA
ANALYSIS
• Definition: Exploratory Data Analysis refers to the critical process of performing
initial investigations on data so as to discover patterns, to spot anomalies, to test
hypothesis and to check assumptions with the help of summary statistics and graphical
representations.
• Do you see what you expect to see?

24. R COMMANDS
data <- read.csv(file="winequality-red.csv", header=T, sep=";")
head(data) – did I read it OK?
str(data) – Am I satisfied with the datatypes?
dim(data) – Dataset size
summary(data) – Summary statistics, missing values?
table(data$quality) – Distribution of class variable

25. CORRPLOT(W, METHOD="CIRCLE", TL.COL="BLACK", TL.SRT=45)
install.packages(“corrplot”)
- Check if correlations make sense.
- Decide on dropping uncorrelated
Variables with the class

26. BOX-PLOTS
g <- list()
j <- 1
long <- melt(data)
for(i in names(data)) {
subdata = long[long$variable == i,]
g[[j]] <- ggplot(data = subdata,
aes(x=variable, y=value)) +
geom_boxplot()
j = j+1
}
grid.arrange(grobs=g, nrow = 2)
- Check outliers

27. DENSITY PLOTS
g <- list()
j <- 1
for(i in names(data)) {
print(i)
p <- ggplot(data = data,
aes_string(x=i)) +
geom_density()
g[[j]] <- p
j = j+1
}
grid.arrange(grobs=g, nrow = 2)
- Check normally distributed or right/positively skewed

28. SIMPLE RULE 6: BE CAREFUL WITH DATA
PREPROCESSING AS WELL

29. IMPUTING
• Imputation: the process of replacing missing data with substituting values
• Calculate statistics on training data, i.e. mean
• Use this mean to replace missing data on both the validation and the testing
datasets
• Same for normalization or standardization
• Normalization sensitive to outliers

30. PROPROCESSING
EXAMPLES IN R
ind <- sample(3, nrow(data), replace=TRUE,
prob=c(0.6, 0.2, 0.2))
trainData <- data[ind==1,]
valData <- data[ind==2,]
testData <- data[ind==3,]
trainMaxs <- apply(trainData[,1:11], 2, max)
trainMins <- apply(trainData[,1:11], 2, min)
normTrainData <-
sweep(sweep(trainData[,1:11], 2, trainMins, "-"),
2, (trainMaxs - trainMins), "/")
summary(normTrainData)

31. PROPROCESSING
EXAMPLES IN R
normValData <- sweep(sweep(valData[,1:11],
2, trainMins, "-"), 2, (trainMaxs - trainMins), "/")
Not an issue if data is big and
correct sampling is kept.

32. SIMPLE RULE 7: DON’T BE UNLUCKY

33. BE KNOWLEDGEABLE
• Aka how randomness affects results…
• If you don’t want to be unlucky do 10 times the 10-fold cross-validation and
average the averages and get precise estimates

34. EXAMPLE IN R
results <- numeric(100)
for(i in 1:100) {
ind <- sample(2, nrow(iris), replace=T,
prob=c(0.9, 0.1))
trainData <- iris[ind==1,]
valData <- iris[ind==2,]
model <- naiveBayes(Species ~ .,
data=trainData)
pred <- predict(model, valData)
results[i] <- Accuracy(pred,
valData$Species)
}
• Even in this simple dataset and
scenario….55/100 splits gave perfect score
in one run.
• With simple 10-fold cross-validation I could
have gotten 100% validation accuracy.
• In one run I got 70%...30% difference
based on luck.

35. SIMPLE RULE 8: TESTING

36. TEST WHICH MODEL IS SUPERIOR
­Depends on what you are doing:
­ If you work in a single dataset and you are in the industry, probably you
go with the model that has the best metric in the validation data, backed
by the testing data metric
­ If you are doing research you can add statistical testing
­ If you are building ML algorithms and you are comparing different
algorithms on a whole lot of datasets, check J. Demsar’s 2006 JMLR paper
(more than 7K citations)

37. CHOOSING BETWEEN TWO
• X and Y models, 10-fold CV
• For a given confidence level, we will check whether the actual difference exceeds
the confidence limit
• Decide on a confidence level: 5% or 1%
• Use Wilcoxon test
• Other tests require more assumptions that are valid with large samples

38. R EXAMPLEresultsMA <- numeric(10)
resultsMB <- numeric(10)
cv <- sample(rep(1:10, nrow(iris)/10))
for(i in 1:10) {
trainData <- iris[cv == i,]
valData <- iris[cv != i,]
model <- naiveBayes(Species ~ ., data=trainData)
pred <- predict(model, valData)
resultsMA[i] <- Accuracy(pred, valData$Species)
ctree = rpart(Species ~ ., data=trainData,
method="class",minsplit = 1, minbucket = 1, cp = -1)
pred <- predict(ctree, valData, type="class")
resultsMB[i] <- Accuracy(pred, valData$Species)
}
wilcoxon.test(resultsMA, resultsMB)
If p value less than confidence level
then there is statistical significance.

39. SIMPLE RULE 9: TIME IS MONEY

40. TIME IS MONEY
• Before doing the whole experimentation, play with a small(er) dataset
• What should this data be?
• Representative!!!
• Check all the pipeline, end-to-end
GPU instances

41. SIMPLE RULE 10: KNOW THY DATA

42. DO I HAVE ENOUGH DATA?
• Learning curves….
• Else augment
• How can one augment?

43. IMAGE
AUGMENTATION
https://github.com/aleju/imgaug

44. SMOTE TO OVERSAMPLE MINORITY CLASS
https://www.researchgate.net/figure/Graphical-representation-of-the-SMOTE-algorithm-a-SMOTE-starts-from-a-set-of-positive_fig2_317489171

45. MORE ANNOTATIONS

46. SIMPLE RULE 11: DECIDE ON YOUR GOAL

47. IS IT INTERPRETABILITY OR PERFORMANCE?
• Decide what are you striving for.
• (Multi)-Collinearity
• X1 = a * X2 + b
• Many different values of the features could predict equally well Y
• Variance Inflation Factor (VIF) test
• 1, no collinearity
• >10, indication of collinearity
• Discussed in: http://kyrcha.info/2019/03/22/on-collinearity-and-feature-selection

48. R EXAMPLE
Miles per gallon prediction, autompg
dataset

49. VIF

50. REMOVE DISPL.

51. VIF AGAIN

52. COMPARISON

53. REMOVE ALL
VIF>10

54. RIDGE REGRESSION
Regularization gives
preference towards one
Solution over the others.

55. RESULTS

56. SIMPLE RULE 12: START BY CHOOSING THE
CORRECT MODEL FOR YOUR PROBLEM

57. RANDOM FORESTS
• Nice algorithm, works on a lot of dataset (Fernandez-Delgado et al., JMLR, 2014)
• Few important parameters to tune
• Handles multiclass problems (unlike for example SVMs)
• Can handle a mixture of features and scales

58. SVM
- Nice algorithm, works on a lot of dataset (Fernandez-Delgado et al., JMLR, 2014)
- Robust theory behind it
- Good for binary classification and 1-class classification
­ We use it in Continuous Implicit Authentication
- Can handle sparse data

59. GRADIENT BOOSTING MACHINES
• Focuses on difficult samples that are hard to learn
• If you have outliers, it will boost them to be the most important points
• So have important outliers and not errors as outliers
• Is more of a black-box, even though it is tree-based
• Needs more tuning
• Easy to overfit
• Mostly better results that RF

60. DEEP LEARNING
• Choose if you have lots of data and computational resources
• Don’t have to throw away anything. Solves the problem end-to-end.

61. SIDENOTE: BIAS - VARIANCE

62. BIAS VS. VARIANCE
Bias: algorithm’s error rate on the training set. Erroneous assumptions in the learning algorithm.
Variance: difference in error rate between training set and validation set. It is caused by
overfitting to the training data and accounting for small fluctuations.
Learning from Data slides:
http://work.caltech.edu/telecourse.html

63. EXAMPLE

64. SIMPLE RULE 13: BECOME A
KNOWLEDGEABLE TRADER

65. BIAS VARIANCE TRADE-OFF HEURISTICS
• #1 High bias => Increase model size (usually with regularization to mitigate high
variance)
• #2 High variance => add training data (usually with a big model to handle them)

66. TRADE FOR BIAS
• Will reduce (avoidable) bias
• Increase model size (more neurons/layers/trees/depth etc.)
• Add more helpful features
• Reduce/remove regularization (L2/L1/dropout)
• Indifferent
•Add more training data

67. TRADE FOR VARIANCE
• Reduce variance
•Add more training data
•Add regularization
•Early stopping (NN)
•Remove features
•Decrease model size (prefer regularization)
• Usually big model to handle training data and then add regularization
•Add more helpful features

68. SIMPLE RULE 14: FINISH OFF WITH AN
ENSEMBLE

69. ENSEMBLE TECHNIQUES
- By now you’ve built a ton of models
- Bagging: RF
- Boosting: AdaBoost, GBT
- Voting/Averaging
- Stacking
Classifier
Classifier
Classifier
Classifier
Classifier
Final Prediction
PredictionsTraining Data

70. SIMPLE RULE 15: TUNE
HYPERPARAMETERS…BUT TO A POINT

71. TUNE THE MOST INFLUENTIAL PARAMETERS
• There is performance to be gained by parameter tuning (Bagnal and Crawley
2017)
• Tons of parameters, we can’t tune them all
• Understand how they influence training + read relevant papers/walkthroughs
• Random forests (Fernandez-Delgado et al., JMLR, 2014)
• mtry: Number of variables randomly sampled as candidates at each split.
• SVM (Fernandez-Delgado et al., JMLR, 2014)
• tuning the regularization and kernel spread

72. SIMPLE RULE 16: START A WATERFALL LIKE
PROCESS

73. THE PROCESS
Study the problem
EDA
Define optimization strategy
(validation, test sets and metric)
Feature Engineering
Modelling
EnsemblingError Analysis

74. GENERAL RULE

75. THE BASIC RECIPE (BY ANDREW NG)
http://t.co/1Rn6q35Qf2

76. THANK YOU
For further AMA questions open an issue at:
https://github.com/kyrcha/ama

77. FURTHER READING
• Personal Experiences
• Various resources over the internet and the years
• ML Yearning: https://www.mlyearning.org/
• Machine Learning from Data course: http://work.caltech.edu/telecourse.html
• Practical Machine Learning with H2O book