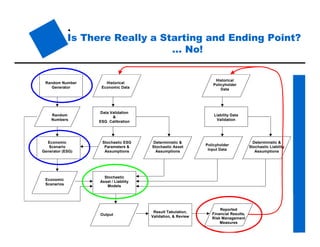
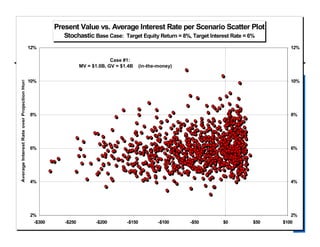
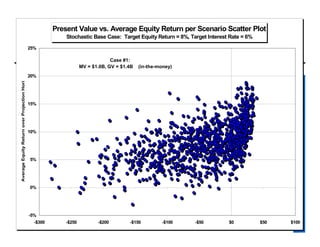
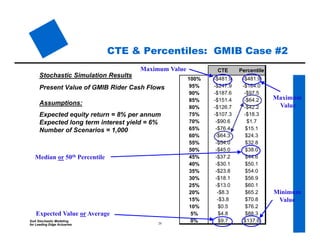
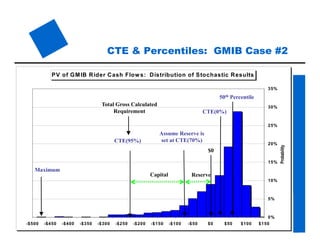
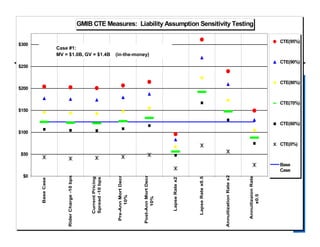
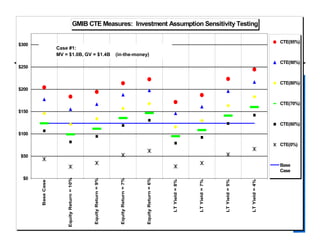
The document provides an overview of stochastic modeling for actuaries. It defines stochastic modeling as a technique that uses random variables and simulations to model complex systems over time. The key advantages are the ability to study long-term outcomes under different scenarios and to better understand risk. Limitations include significant effort required and reliance on input assumptions. Stochastic modeling is preferred when risks are complex or path dependent. The document outlines the modeling steps and discusses concepts like the conditional tail expectation.

1. SoA Stochastic Modeling
for Leading Edge Actuaries 1
Stochastic Modeling for
Leading Edge Actuaries
Overview of the Practical Aspects of
Stochastic Modeling
Ron Harasym MBA, CFA, FSA, FCIA
Vice-President & Chief Risk Officer

2. SoA Stochastic Modeling
for Leading Edge Actuaries 2
Outline of Presentation
 Stochastic Modeling Defined.
 What Stochastic Modeling is and isn’t.
 Advantages and Limitations of Stochastic Modeling.
 When Stochastic Modeling is Preferred.
 Key steps in Stochastic Modeling
 Conditional Tail Expectation & Examples
 Recommended Practices
 Final Thoughts

3. SoA Stochastic Modeling
for Leading Edge Actuaries 3
Stochastic Modeling - Definition
 Stochastic [Greek stokhastikos: from stokhasts, diviner, from
stokhazesthai, to guess at, from stokhos, aim, goal.]
 A stochastic model by definition has at least one random
variable and deals explicitly with time-variable interaction.
 A stochastic simulation uses a statistical sampling of multiple
replicates, repeated simulations, of the same model.
 Such simulations are also sometimes referred to as Monte
Carlo simulations because of their use of random variables.

4. SoA Stochastic Modeling
for Leading Edge Actuaries 4
Stochastic Modeling - What it is
 A stochastic model is an imitation of a real world system. An
imprecise technique that provides statistical estimates and not
exact results.
 Stochastic modeling serves as a tool in a company’s risk
measurement toolkit to provide assistance in:
 Valuation, Forecasting, Solvency Testing
 Financial Reporting
 Product Design & Pricing
 Risk Management
 Simulations are used when the systems being modeled are too
complex to be described by a set of mathematical equations for
which a closed form analytic solution is readily attainable.
 Part art, part science, part judgement, part common sense.

5. SoA Stochastic Modeling
for Leading Edge Actuaries 5
Stochastic Modeling - And What it isn’t
 Not a magical solution! One needs to:
 Perform reality checks
 Understand strengths & limitations of the model
 Results are not always intuitively obvious!
 Often requires a different way of looking at problems, issues,
results, and potential solutions.
 Greater exposure to model risk and operational risks.

6. SoA Stochastic Modeling
for Leading Edge Actuaries 6
Advantages of Stochastic Modeling
 Systems with long time frames can be studied in compressed time.
 Able to assist in decision making and to quantify future outcomes
arising from different actions/strategies before implementation.
 Can attempt to better understand properties of real world systems
such as policyholder behavior.
 Quantification of the benefit from risk diversification.
 Coherent articulation of risk profiles.
 Potential reserve and regulatory capital relief.

7. SoA Stochastic Modeling
for Leading Edge Actuaries 7
Limitations of Stochastic Modeling
 Requires a considerable investment of time and expertise.
 Technically challenging, computationally demanding.
 Reliance on a few “good” people!
 For any given set of inputs, each scenario gives only a estimate.
 May create a false sense of confidence - a false sense of
precision let alone a false sense of accuracy.
 Relies heavily on data inputs and the identification of variable
interactions.
 It is not possible to include all future events in a model.
 Results may be difficult to interpret.
 Effective communication of results may be even more difficult.
 Garbage in, Garbage out!

8. SoA Stochastic Modeling
for Leading Edge Actuaries 8
Stochastic modeling is Preferred over
Deterministic Modeling When:
 Product or Line of Business has a “cliff” or “tail” risk profile.
 Risks are dependent and/or there is path dependence.
 When dealing with skewed and/or discontinuous distributions/cost
functions.
 Outcomes are sensitive to initial conditions.
 There is significant volatility in the underlying variables.
 Volatility or skewness of underlying variables is likely to change
over time.
 There are real economic incentives, such as reserve or capital
relief, to perform stochastic modeling.

9. SoA Stochastic Modeling
for Leading Edge Actuaries 9
Is There Really a Starting and Ending Point?
… No!
Output
Historical
Economic Data
Historical
Policyholder
Data
Random Number
Generator
Economic
Scenario
Generator (ESG)
Stochastic ESG
Parameters &
Assumptions
Policyholder
Input Data
Economic
Scenarios
Data Validation
&
ESG Calibration
Random
Numbers
Stochastic
Asset / Liability
Models
Liability Data
Validation
Deterministic &
Stochastic Liability
Assumptions
Deterministic &
Stochastic Asset
Assumptions
Result Tabulation,
Validation, & Review
Reported
Financial Results,
Risk Management
Measures

10. SoA Stochastic Modeling
for Leading Edge Actuaries 10
Where does one Start? Key Steps Are ...
 Identify the key issues, objectives and potential roadblocks
before considering ways of solving the problem.
 Articulate the process / model in general terms before
proceeding to the specific.
 Develop the model: assumptions, input parameters, data,
output.
 Fit the model: gather and analyze data, estimate input
parameters
 Implement the model.
 Analyze and test sensitivity of the model results & loop back.
 Communicate the results.

11. SoA Stochastic Modeling
for Leading Edge Actuaries 11
Points to Keep in Mind!
 Stochastic modeling is an evolutionary / revolutionary concept.
 There must be a constant feedback loop.
 Learn to “walk” before you “run”.
 Recognize that no one model fits all solutions.
 Be careful of becoming “married to the method”, rather than the
objective.
 Keep it simple, keep it practical, keep it understandable.
 Keep performing validation and reality checks throughout all
modeling steps.
 Strive towards the production of actionable information!

12. SoA Stochastic Modeling
for Leading Edge Actuaries 12
Conditional Tail Expectation
 Conditional Tail Expectation (CTE) is a conditional expected value
based on downside risk.
 CTE can be defined as the average of outcomes that exceed a
specified percentile.
 The CTE(Q%) is calculated as the arithmetic average of the worst
(100-Q)% results of the stochastic simulation.
 For example: CTE(75%) is the arithmetic average of the worst
25% of the results of the stochastic simulation.
 CTE is considered to be a more robust measure with greater
information content than percentiles.
 The CTE measure can also be “modified”.

13. SoA Stochastic Modeling
for Leading Edge Actuaries 13
Random Number Generator
 Objective:
 To produce random numbers between 0 and 1
 Issues:
 The Random Number Generator (RNG) is a foundation building block
 Critical, but often ignored/forgotten about!
 Poor RNG can compromise all post modeling sophistication
 Numerous RNGs to choose from
 Desirable Characteristics to check for:
 Robustness independent of the seed number
 Periodicity
 Fast, efficient, & effective algorithm
 Other statistical tests (an internet search will provide many)

14. SoA Stochastic Modeling
for Leading Edge Actuaries 14
Economic Scenario Generator
 Objective:
 To produce capital market or economic scenarios
 Components:
 Drift, Diffusion, Correlation, …
 Issues:
 Is the focus on the mean, median, or tail events?
 What metric is of concern?
 Economic vs. Statistical model, Arbitrage-Free vs. Equilibrium
 What is our calibration benchmark?
 Numerous ESGs to choose from
 Desirable Characteristics to check for:
 Integrated model (equity, interest rate, inflation, currency)
 Incorporates the principle of parsimony.
 Flexible. A component approach.

15. SoA Stochastic Modeling
for Leading Edge Actuaries 15
Calibration of the
Economic Scenario Generator
 Stability of the components over time
 Drift Stability versus Diffusion Stability versus Correlation Stability
 Frequency of recalibration
 Historical data period versus forecast horizon
 Selection of lead index
 Selection of starting regime if using a multiple regime model
 Foreign exchange Issues
 Data sources and Caveat Emptor
 Approaches to fitting the data
 Risk-Return relationship
 False sense of precision and subjectivity

16. SoA Stochastic Modeling
for Leading Edge Actuaries 16
Example: Variable Annuity GMIB Rider
 Product:
 Guaranteed Minimum Income Benefit Rider
 Objective:
 Produce Measures for Financial Reporting
 Calculate Reserve & Capital Requirements
 Nature of the Situation:
 Case #1: MV = $1.00B, GV = $1.40B (in-the-money)
 Case #2: MV = $2.75B, GV = $2.75B (at-the-money)
 Mixture of policyholders
 5% Roll-up rate per annum
 Conservative interest and mortality assumptions at time of product
pricing

17. SoA Stochastic Modeling
for Leading Edge Actuaries 17
Economic Scenario Generation
 Economic Scenario Generator:
 Equity returns modeled using RSLN2 model
 Fixed Income returns modeled using Cox-Ingersol-Ross model
 Correlated Equity & Fixed Income Returns
 Calibration Method:
 Maximum Likelihood Estimation
 Calibration Issues:
 Data is limited and often inconsistent/incorrect.
 Insufficient effort is often given to data validation.
 Requires complex methods
 Historical data period versus forecast horizon
 Frequency of recalibration
 Simulation:
 1000 scenarios, monthly frequency,
30 year projection horizon

18. SoA Stochastic Modeling
for Leading Edge Actuaries 18
Present Value vs. Average Interest Rate per Scenario Scatter Plot
Stochastic Base Case: Target Equity Return = 8%, Target Interest Rate = 6%
2%
4%
6%
8%
10%
12%
-$300 -$250 -$200 -$150 -$100 -$50 $0 $50 $100
AverageInterestRateoverProjectionHorizon
2%
4%
6%
8%
10%
12%
Case #1:
MV = $1.0B, GV = $1.4B (in-the-money)

19. SoA Stochastic Modeling
for Leading Edge Actuaries 19
Present Value vs. Average Equity Return per Scenario Scatter Plot
Stochastic Base Case: Target Equity Return = 8%, Target Interest Rate = 6%
-5%
0%
5%
10%
15%
20%
25%
-$300 -$250 -$200 -$150 -$100 -$50 $0 $50 $100
AverageEquityReturnoverProjectionHorizon
Case #1:
MV = $1.0B, GV = $1.4B (in-the-money)

20. SoA Stochastic Modeling
for Leading Edge Actuaries 20
CTE Percentile
100% -$481.9 -$481.9
95% -$247.9 -$164.0
90% -$187.6 -$97.5
85% -$151.4 -$64.2
80% -$126.7 -$42.2
75% -$107.3 -$18.3
70% -$90.6 $1.7
65% -$76.4 $15.1
60% -$64.3 $24.3
55% -$54.0 $32.8
50% -$45.0 $38.0
45% -$37.2 $44.6
40% -$30.1 $50.1
35% -$23.8 $54.0
30% -$18.1 $56.9
25% -$13.0 $60.1
20% -$8.3 $65.2
15% -$3.8 $70.8
10% $0.5 $76.2
5% $4.8 $88.3
0% $9.7 $137.6
CTE & Percentiles: GMIB Case #2
Stochastic Simulation Results
Present Value of GMIB Rider Cash Flows
Assumptions:
Expected equity return = 8% per annum
Expected long term interest yield = 6%
Number of Scenarios = 1,000
Expected Value or Average
Median or 50th Percentile
Maximum Value
Maximum
Value
Minimum
Value

21. SoA Stochastic Modeling
for Leading Edge Actuaries 21
PV of GMIB Rider Cash Flow s: Distribution of Stochastic Results
0%
5%
10%
15%
20%
25%
30%
35%
-$500 -$450 -$400 -$350 -$300 -$250 -$200 -$150 -$100 -$50 $0 $50 $100 $150
Probability
CTE(0%)
50th Percentile
Assume Reserve is
set at CTE(70%)CTE(95%)
Capital
$0
Reserve
Total Gross Calculated
Requirement
Maximum
CTE & Percentiles: GMIB Case #2

22. SoA Stochastic Modeling
for Leading Edge Actuaries 22
Sensitivity/Stress Testing
 Quantifies the impact of an immediate change in an
assumption or variable.
 Useful for validation of the model with respect to individual
assumptions
 Also a check on the modeled variable interactions
 Allows one to identify and thereby direct more effort on key
assumptions or variables.

23. SoA Stochastic Modeling
for Leading Edge Actuaries 23
GMIB CTE Measures: Liability Assumption Sensitivity Testing
$0
$50
$100
$150
$200
$250
$300 BaseCase
RiderCharge-10bps
CurrentPricing
Spread-10bps
Pre-AnnMortDecr
10%
Post-AnnMortDecr
10%
LapseRatex2
LapseRatex0.5
AnnuitizationRatex2
AnnuitizaionRate
x0.5
CTE(95%)
CTE(90%)
CTE(80%)
CTE(70%)
CTE(60%)
CTE(0%)
Base
Case
Case #1:
MV = $1.0B, GV = $1.4B (in-the-money)

24. SoA Stochastic Modeling
for Leading Edge Actuaries 24
GMIB CTE Measures: Investment Assumption Sensitivity Testing
$0
$50
$100
$150
$200
$250
$300 BaseCase
EquityReturn=10%
EquityReturn=9%
EquityReturn=7%
EquityReturn=6%
LTYield=8%
LTYield=7%
LTYield=5%
LTYield=4%
CTE(95%)
CTE(90%)
CTE(80%)
CTE(70%)
CTE(60%)
CTE(0%)
Base
Case
Case #1:
MV = $1.0B, GV = $1.4B (in-the-money)

25. SoA Stochastic Modeling
for Leading Edge Actuaries 25
Recommended Practices:
 Keep focused on the business objectives.
 No one model fits all. Best to understand fundamentals.
 Cultivate “best practices”.
 Keep it simple and practical.
 Focus on accuracy first, precision second.
 Add complexity on a cost/benefit basis.
 Don’t ignore data validation and model validation procedures.
 Continually perform reality checks.
 Constantly loop back through the process.

26. SoA Stochastic Modeling
for Leading Edge Actuaries 26
Other Issues to Wrestle With:
 Some model set-ups generate more volatility in results than
others. How do we choose between them?
 How do we perform calibration and parameter estimation?
 How do we capture the correlations between markets.
 How many scenarios do we use?
 How do we model policyholder behaviour?
 How do we incorporate hedging in the model?

27. SoA Stochastic Modeling
for Leading Edge Actuaries 27
Finally, Where Are We Going … ???
 Will stochastic modeling change the way the insurance industry
conducts business?
 What will be the impact of the recent acceptance/application of
stochastic modeling within the next 1, 5, 10+ years?
 How will stochastic modeling alter/impact pricing, product
development, and valuation / risk management practices &
procedures?
 Even closer to home, how will stochastic modeling impact the
educational experience and skill requirements of current and
future actuaries?

28. SoA Stochastic Modeling
for Leading Edge Actuaries 28
Wrap-Up
Questions & Answers!