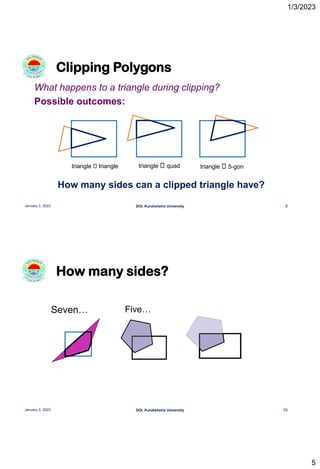
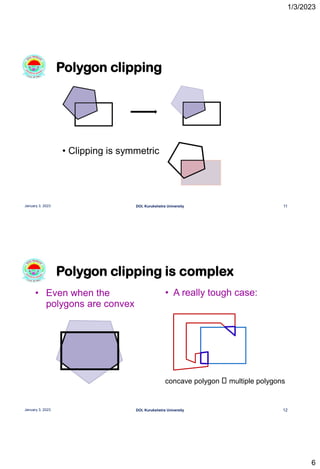
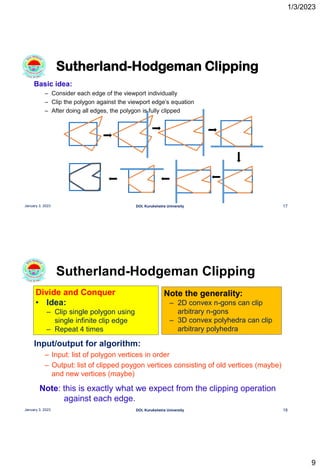
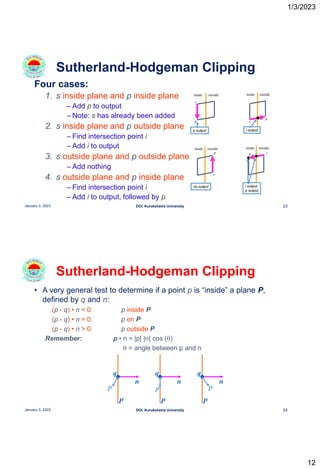
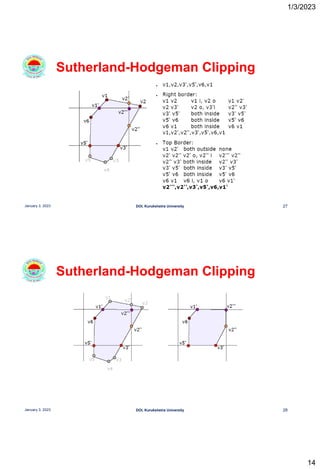
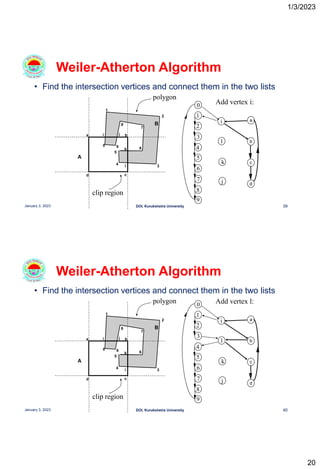
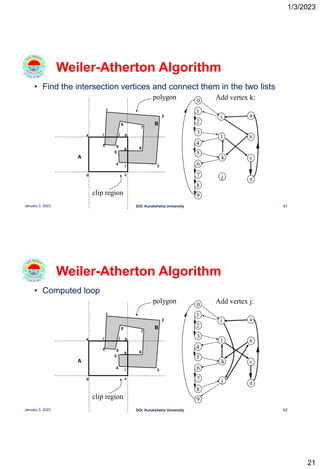
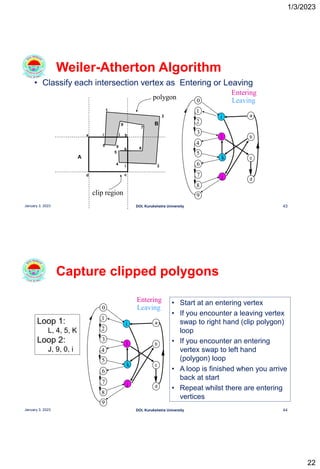
This document discusses polygon clipping algorithms in computer graphics. It begins with an overview of polygon clipping and some of the challenges, such as producing multiple polygons from a single clipped polygon. It then describes the Sutherland-Hodgman clipping algorithm in detail, including the four cases used to clip edges. Issues with this algorithm for concave polygons are noted. The document concludes by explaining the Weiler-Atherton clipping algorithm, which produces separate polygons to address issues with the Sutherland-Hodgman approach.