Downloaded 11 times
Uploaded byJenChing Teoh
Sistem persamaan linear
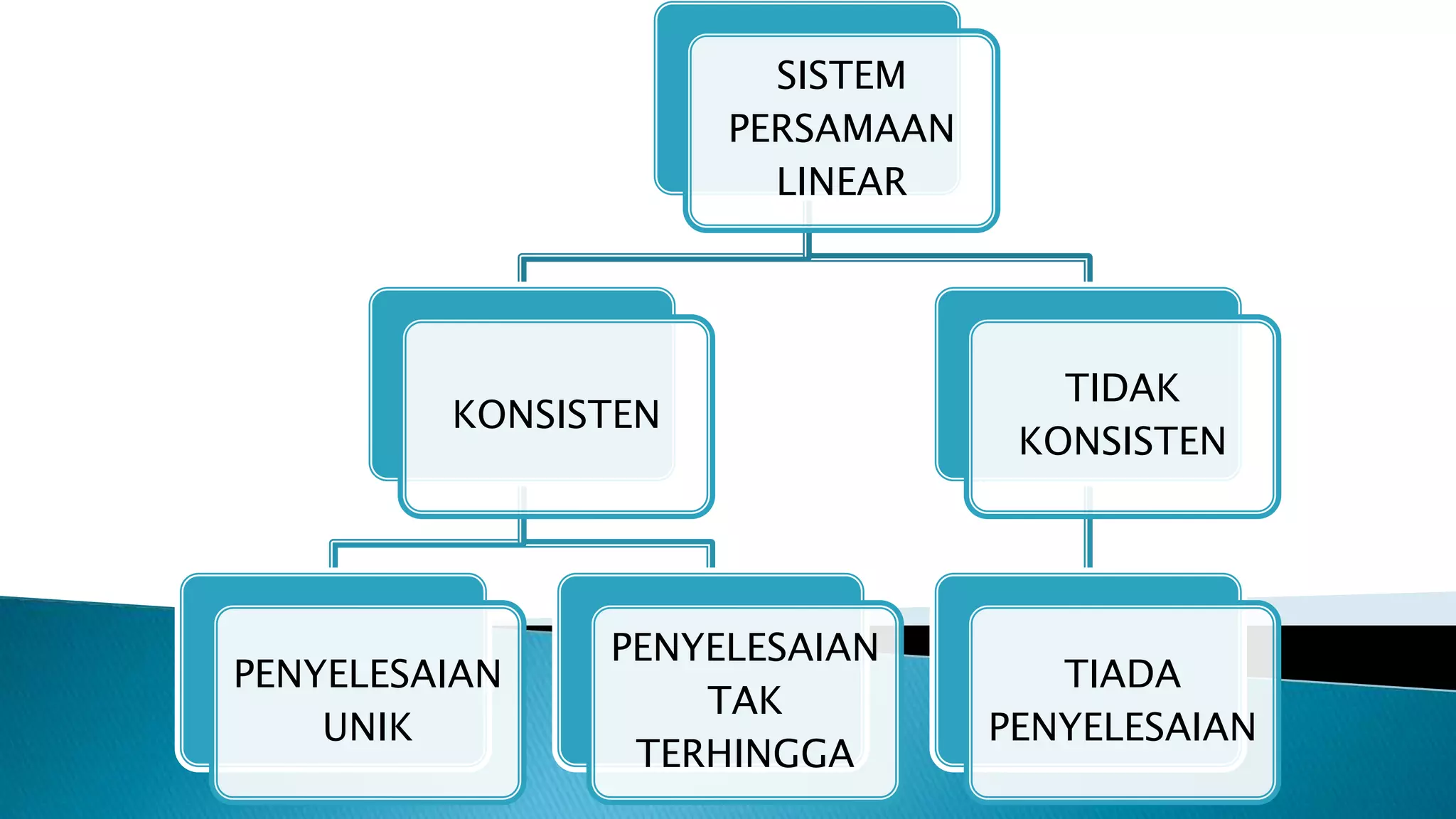
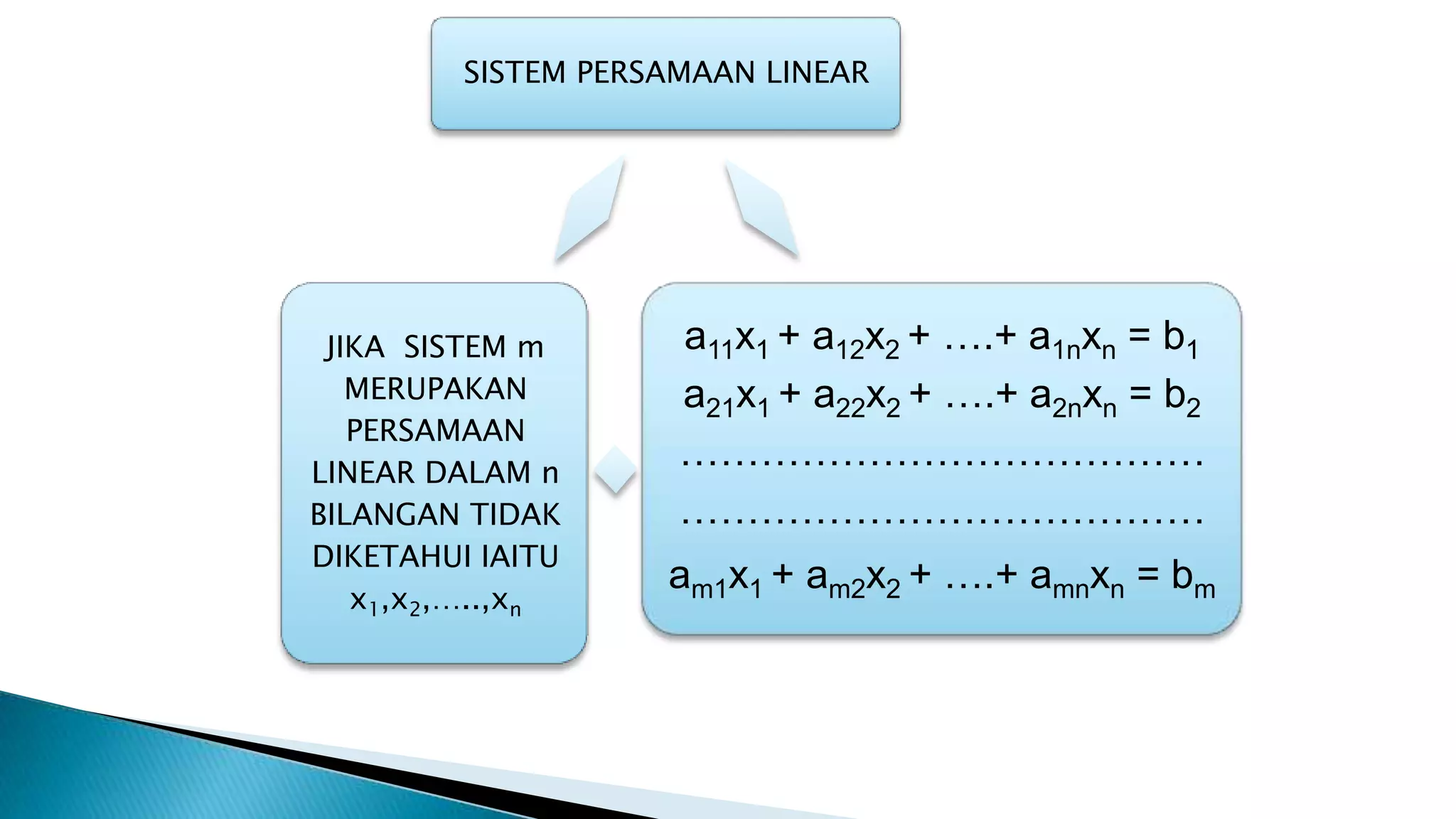
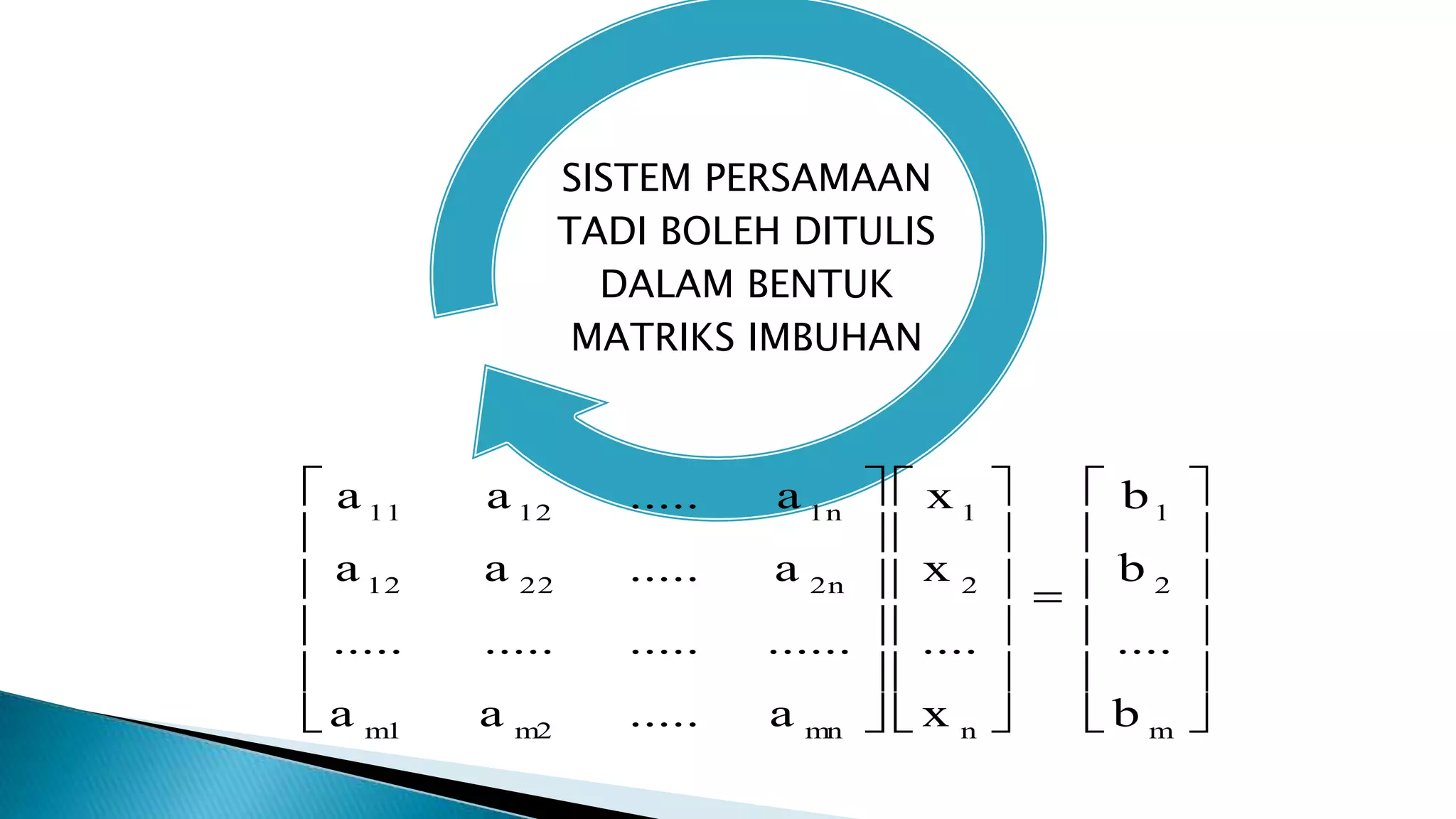
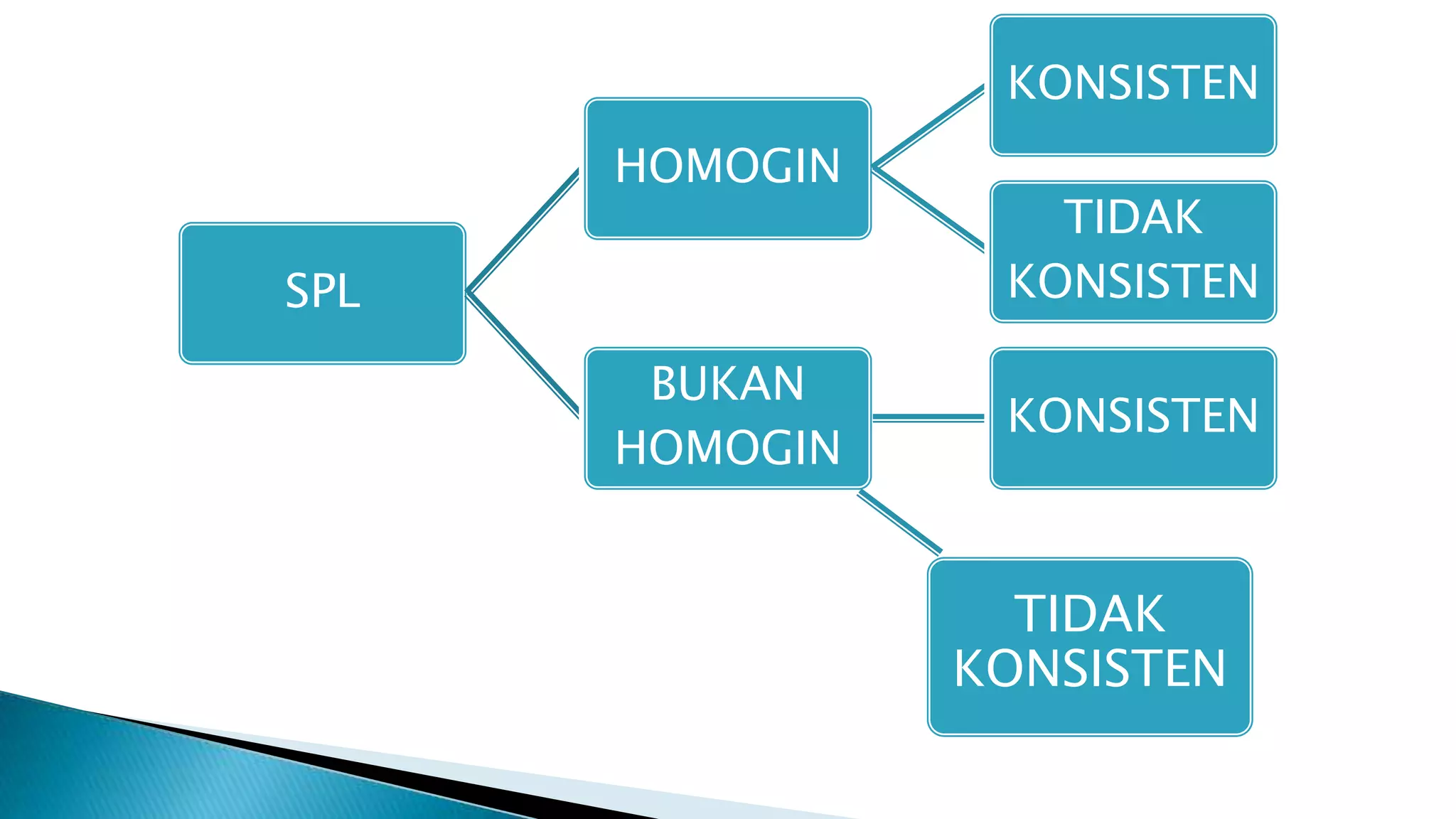
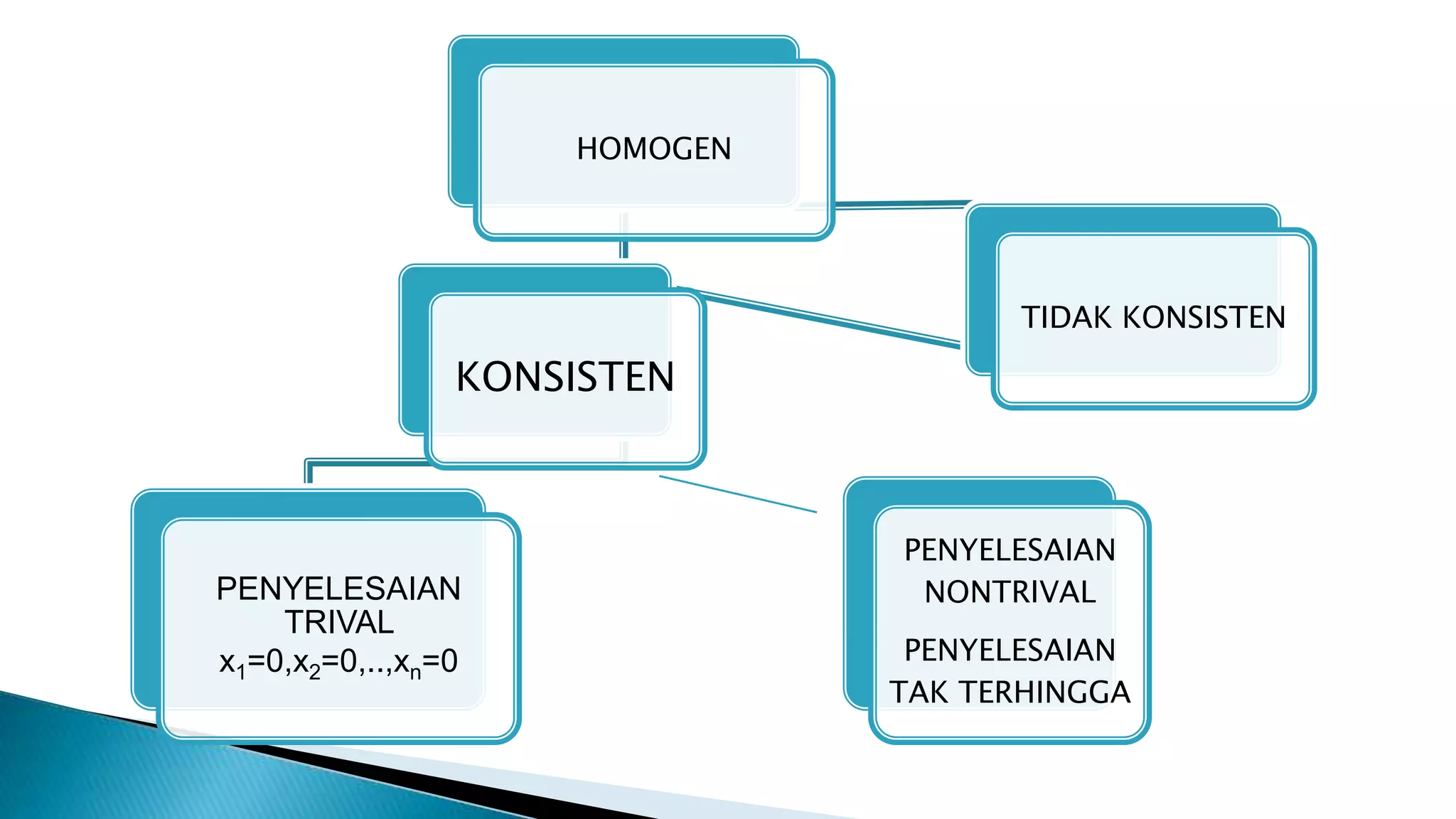
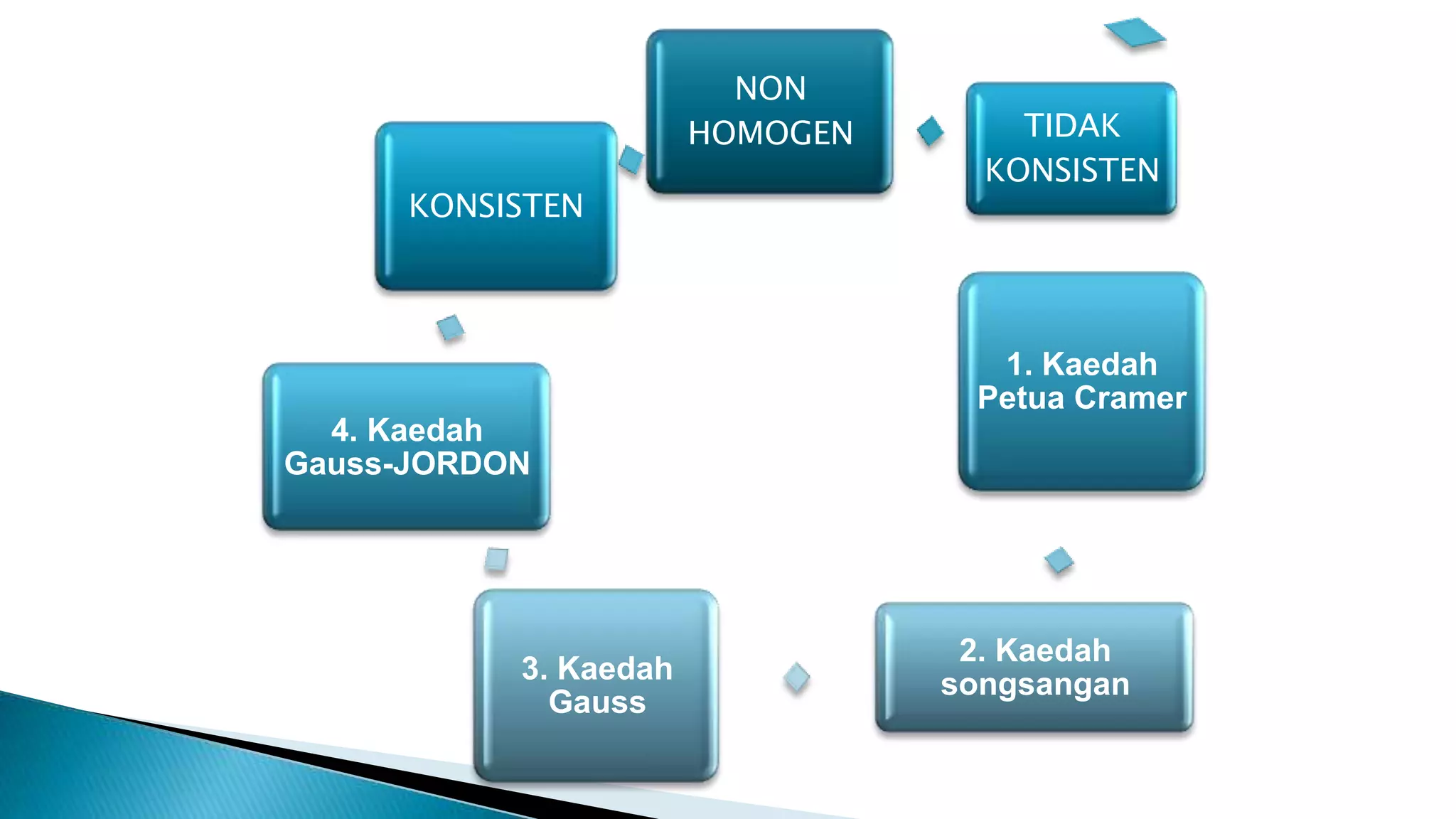
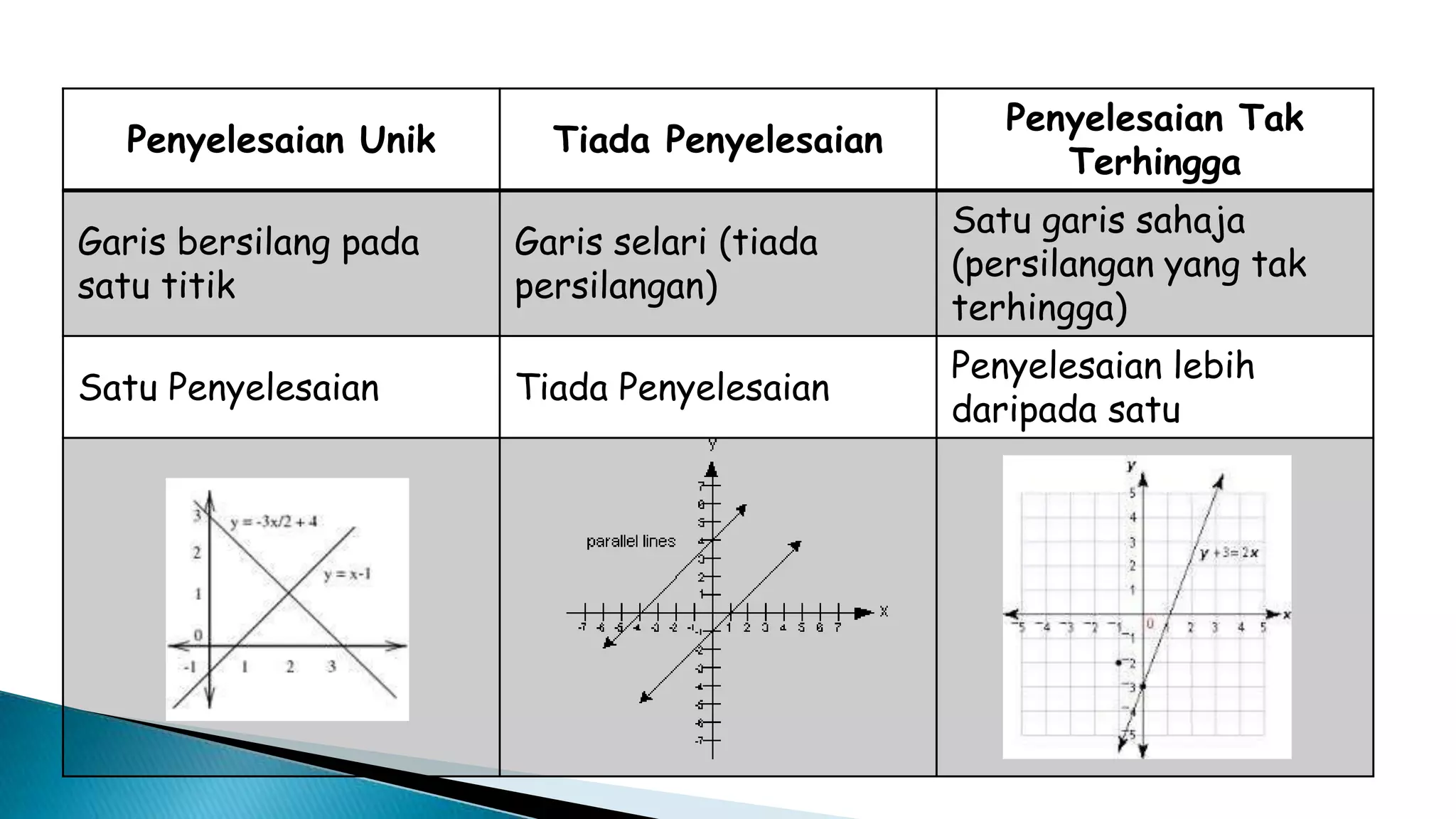
Persamaan linear adalah persamaan darjah pertama yang membentuk garis lurus, dan sistem persamaan linear boleh terdiri daripada penyelesaian unik, tiada penyelesaian, atau penyelesaian tak terhingga. Terdapat pelbagai kaedah untuk menyelesaikan sistem ini, termasuk kaedah Cramer dan kaedah Gauss. Keadaan penyelesaian bergantung pada interaksi antara garis-garis yang dibentuk oleh persamaan tersebut.
Sistem persamaan linear
- 2. Persamaan Linearialah persamaan untuk satu garis lurus yang kuasa tertingginya ialah satu(1), darjah pertama Sistem Persamaan Linear wujud ketika terdapat dua atau lebih persamaan
- 3.
- 4. SISTEM PERSAMAAN LINEAR a11x1+ a12x2 + ….+ a1nxn = b1 a21x1 + a22x2 + ….+ a2nxn = b2 ………………………………… ………………………………… am1x1 + am2x2 + ….+ amnxn = bm JIKA SISTEM m MERUPAKAN PERSAMAAN LINEAR DALAM n BILANGAN TIDAK DIKETAHUI IAITU x1,x2,…..,xn
- 5. SISTEM PERSAMAAN TADI BOLEHDITULIS DALAM BENTUK MATRIKS IMBUHAN m 2 1 n 2 1 mnm2m1 2n2212 1n1211 b .... b b x .... x x a.....aa ..................... a.....aa a.....aa
- 6.
- 7.
- 8. NON HOMOGEN TIDAK KONSISTEN 1. Kaedah PetuaCramer 2. Kaedah songsangan3. Kaedah Gauss 4. Kaedah Gauss-JORDON KONSISTEN
- 9. Untuk mendapatkannilai pembolehubah Terdapat 3 kemungkinan Penyelesaian Unik Tiada Penyelesaian Penyelesaian Tidak terhingga
- 10. Wujud ketikadua atau garis tersebut bersilang pada satu titik sahaja Satu titik persilangan=satu penyelesaian=penyelesaian unik
- 11. Wujud ketika2 atau lebih garis lurus yang terlibat dalam keadaan selari Seperti dalam gambar rajah, garis selari tidak pernah bertemu. Oleh itu, tiada wujud Penyelesaian
- 12. Wujud ketikagaris-garis tersebut bertindih Bersilang di bilangan titik yang tak terhingga Penyelesaian tidak unik=lebih daripada satu penyelesaian/penyelesaian tak terhingga
- 13. Penyelesaian Unik TiadaPenyelesaian Penyelesaian Tak Terhingga Garis bersilang pada satu titik Garis selari (tiada persilangan) Satu garis sahaja (persilangan yang tak terhingga) Satu Penyelesaian Tiada Penyelesaian Penyelesaian lebih daripada satu